第19页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
- 第138页
- 第139页
- 第140页
- 第141页
- 第142页
- 第143页
- 第144页
- 第145页
- 第146页
- 第147页
- 第148页
- 第149页
- 第150页
8. (2025·益阳期末)已知数轴上点A,B的位置如图所示,点A表示的有理数为$a$,点B表示的有理数为$b$,$m = a + b$,则比$m$大的最小整数为(
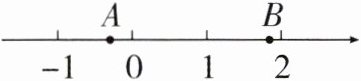
A.$1$
B.$2$
C.$3$
D.$4$
B
)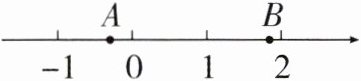
A.$1$
B.$2$
C.$3$
D.$4$
答案:
B 解析:由题图得,$-\frac{1}{2} < a < 0$,$\frac{3}{2} < b < 2$,所以 $1 < a + b < 2$. 因为 $m = a + b$,所以 $1 < m < 2$,比 $m$ 大的最小整数为 2. 故选 B.
9. 若非零数$a$,$b满足| a + b | = | a | + | b |$,则(
A.$a$,$b$均为正数
B.$a$,$b$均为负数
C.$a$,$b$异号
D.$a$,$b$同号
D
)A.$a$,$b$均为正数
B.$a$,$b$均为负数
C.$a$,$b$异号
D.$a$,$b$同号
答案:
D 解析:当 $a$,$b$ 均为正数时,$|a + b| = a + b$,$|a| + |b| = a + b$,满足题意;当 $a$,$b$ 均为负数时,$|a + b| = -a - b$,$|a| + |b| = -a - b$,即 $|a + b| = |a| + |b|$,满足题意;当 $a$ 为正数,$b$ 为负数时,$|a + b| = a + b$ 或 $|a + b| = -a - b$,$|a| + |b| = a - b$,两者不相等,不符合题意;同理可知,当 $a$ 为负数,$b$ 为正数时,不符合题意. 综上,$a$,$b$ 同号等式成立,故选 D.
10. 小颖同学做这样一道题:计算$| - 4 + \triangle |$.其中“$\triangle$”是被墨水污染看不清的一个数,她翻开后面的答案,得知该题的计算结果是$3$,那么“$\triangle$”表示的数是
7 或 1
.
答案:
7 或 1 解析:由题可知,$|-4 + \triangle| = 3$,即 $-4 + \triangle = 3$ 或 $-4 + \triangle = -3$,解得 $\triangle = 7$ 或 $\triangle = 1$.
11. 新题型 新定义 设用符号$( a , b )表示a$,$b$两数中较小的数,用符号$[ a , b ]表示a$,$b$两数中较大的数,试求下列各式的值.
(1)$( - 5 , - 0.5 ) + [ - 4,2 ] = $
(2)$\left( - 1 \frac { 1 } { 2 } , 3 \right) + \left[ - 4 , \left( - \frac { 11 } { 3 } , - 7 \right) \right] =$
(1)$( - 5 , - 0.5 ) + [ - 4,2 ] = $
-3
.(2)$\left( - 1 \frac { 1 } { 2 } , 3 \right) + \left[ - 4 , \left( - \frac { 11 } { 3 } , - 7 \right) \right] =$
$-5\frac{1}{2}$
.
答案:
(1)-3 解析:$(-5, -0.5) + [-4, 2] = -5 + 2 = -3$.
(2)$-5\frac{1}{2}$ 解析:$\left(-1\frac{1}{2}, 3\right) + \left[-4, \left(-\frac{11}{3}, -7\right)\right] = -1\frac{1}{2} + [-4, -7] = -1\frac{1}{2} + (-4) = -5\frac{1}{2}$.
(1)-3 解析:$(-5, -0.5) + [-4, 2] = -5 + 2 = -3$.
(2)$-5\frac{1}{2}$ 解析:$\left(-1\frac{1}{2}, 3\right) + \left[-4, \left(-\frac{11}{3}, -7\right)\right] = -1\frac{1}{2} + [-4, -7] = -1\frac{1}{2} + (-4) = -5\frac{1}{2}$.
12. (1)已知$| a | = 5$,$| b | = 2$,且$a > b$,则$a + b$的值为
(2)已知$| a | = 4$,$| b | = 3$,且$| a - b | = b - a$,则$a + b$的值为
7 或 3
.(2)已知$| a | = 4$,$| b | = 3$,且$| a - b | = b - a$,则$a + b$的值为
-1 或 -7
.
答案:
(1)7 或 3 解析:因为 $|a| = 5$,$|b| = 2$,且 $a > b$,所以 $a = 5$,$b = \pm 2$,故 $a + b = 7$ 或 $a + b = 3$.
(2)-1 或 -7 解析:因为 $|a| = 4$,$|b| = 3$,所以 $a = \pm 4$,$b = \pm 3$. 因为 $|a - b| = b - a$,所以 $a - b \leq 0$,即 $a \leq b$,所以当 $a = -4$,$b = -3$ 时,$a + b = -4 + (-3) = -7$,当 $a = -4$,$b = 3$ 时,$a + b = -4 + 3 = -1$. 综上,$a + b$ 的值为 -1 或 -7.
(1)7 或 3 解析:因为 $|a| = 5$,$|b| = 2$,且 $a > b$,所以 $a = 5$,$b = \pm 2$,故 $a + b = 7$ 或 $a + b = 3$.
(2)-1 或 -7 解析:因为 $|a| = 4$,$|b| = 3$,所以 $a = \pm 4$,$b = \pm 3$. 因为 $|a - b| = b - a$,所以 $a - b \leq 0$,即 $a \leq b$,所以当 $a = -4$,$b = -3$ 时,$a + b = -4 + (-3) = -7$,当 $a = -4$,$b = 3$ 时,$a + b = -4 + 3 = -1$. 综上,$a + b$ 的值为 -1 或 -7.
13. (2025·唐山期末)我国自主研发的巡逻机器人备受关注,为安保工作提供了强有力的支持.某天小明发现一个巡逻机器人正准备在一条南北方向的公路上执行治安巡逻.(规定初始位置为$0$,向北走为正,向南走为负)它从初始位置到结束巡逻所走的路程(单位:$\mathrm { km }$)如下:
|次数|第一次|第二次|第三次|第四次|第五次|第六次|
|路程/$\mathrm { km }$|$+ 2$|$- 1.5$|$+ 4.5$|$- 2$|$+ 0.5$|$- 1.5$|
(1)直接写出巡逻机器人在这次巡逻中离出发点最远的距离为____$\mathrm { km }$;
(2)通过计算,描述巡逻机器人结束巡逻时的最后位置;
(3)已知这次巡逻机器人的平均速度为$3 \mathrm { km } / \mathrm { h }$,请求出巡逻机器人的巡逻时间.
(1)
(2)
(3)
|次数|第一次|第二次|第三次|第四次|第五次|第六次|
|路程/$\mathrm { km }$|$+ 2$|$- 1.5$|$+ 4.5$|$- 2$|$+ 0.5$|$- 1.5$|
(1)直接写出巡逻机器人在这次巡逻中离出发点最远的距离为____$\mathrm { km }$;
(2)通过计算,描述巡逻机器人结束巡逻时的最后位置;
(3)已知这次巡逻机器人的平均速度为$3 \mathrm { km } / \mathrm { h }$,请求出巡逻机器人的巡逻时间.
(1)
5
(2)
$+2 - 1.5 + 4.5 - 2 + 0.5 - 1.5 = 2(km)$,所以巡逻机器人结束巡逻时的最后位置在出发点北面 2 km 处.
(3)
此次巡逻共走 $|+2| + |-1.5| + |+4.5| + |-2| + |+0.5| + |-1.5| = 12(km)$,$12 ÷ 3 = 4(h)$,所以巡逻机器人的巡逻时间是 4 h.
答案:
(1)5 解析:第一次:+2 km;第二次:$+2 - 1.5 = 0.5(km)$;第三次:$0.5 + 4.5 = 5(km)$;第四次:$5 - 2 = 3(km)$;第五次:$3 + 0.5 = 3.5(km)$;第六次:$3.5 - 1.5 = 2(km)$;所以巡逻机器人在这次巡逻中离出发点最远的距离为 5 km.
(2)$+2 - 1.5 + 4.5 - 2 + 0.5 - 1.5 = 2(km)$,所以巡逻机器人结束巡逻时的最后位置在出发点北面 2 km 处.
(3)此次巡逻共走 $|+2| + |-1.5| + |+4.5| + |-2| + |+0.5| + |-1.5| = 12(km)$,$12 ÷ 3 = 4(h)$,所以巡逻机器人的巡逻时间是 4 h.
(1)5 解析:第一次:+2 km;第二次:$+2 - 1.5 = 0.5(km)$;第三次:$0.5 + 4.5 = 5(km)$;第四次:$5 - 2 = 3(km)$;第五次:$3 + 0.5 = 3.5(km)$;第六次:$3.5 - 1.5 = 2(km)$;所以巡逻机器人在这次巡逻中离出发点最远的距离为 5 km.
(2)$+2 - 1.5 + 4.5 - 2 + 0.5 - 1.5 = 2(km)$,所以巡逻机器人结束巡逻时的最后位置在出发点北面 2 km 处.
(3)此次巡逻共走 $|+2| + |-1.5| + |+4.5| + |-2| + |+0.5| + |-1.5| = 12(km)$,$12 ÷ 3 = 4(h)$,所以巡逻机器人的巡逻时间是 4 h.
14. 小丽在$4$张同样的纸片上各写了一个正整数,从中随机抽取$2$张,并将它们上面的数相加.重复这样做,每次所得的和都是$5$,$6$,$7$,$8$中的一个数,并且这$4$个数都能取到.猜猜看,小丽在$4$张纸片上各写下的数是
2, 3, 3, 5 或 2, 3, 4, 4
.
答案:
2, 3, 3, 5 或 2, 3, 4, 4 解析:若这 4 个数从小到大排列分别为 $a$,$b$,$c$,$d$. ①当 4 个数中最小的数 $a$ 为 1 时,因为 $1 + 4 = 5$,所以 $b = 4$. 因为 $1 + 5 = 6$,$4 + 2 = 6$,所以 $c$ 只能为 5,此时 $b + c = 9$,不符合题意. ②当 4 个数中最小的数 $a$ 为 2 时,因为 $2 + 3 = 5$,所以 $b = 3$. 因为 $2 + 4 = 6$,$3 + 3 = 6$,所以 $c = 3$ 或 $c = 4$,当 $c = 3$ 时,$d = 5$,当 $c = 4$ 时,$d = 4$. ③当 4 个数中最小的数 $a$ 为 3 或大于 3 的整数时,无法得出和为 5 的结果,不符合题意. 综上所述,四个数分别为 2, 3, 3, 5 或 2, 3, 4, 4.
15. 还记得小时候经常玩的填数游戏吗?一起用有理数来试试吧!
(1)请在图①的各个圆圈内填上适当的数,使每个圆圈内的数都等于与它相邻的两个数的和;
(2)如图②,在$3 × 3$的方格中补全数字,使得每行、每列、每条对角线上的三个数之和相等;
(3)如图③,请将$2$,$3$,$4$,$5$,$6$,$7$,$8$,$9$,$10填入3 × 3$的方格中,使得每行、每列、每条对角线上的三个数之和相等.

(1)请在图①的各个圆圈内填上适当的数,使每个圆圈内的数都等于与它相邻的两个数的和;
(2)如图②,在$3 × 3$的方格中补全数字,使得每行、每列、每条对角线上的三个数之和相等;
(3)如图③,请将$2$,$3$,$4$,$5$,$6$,$7$,$8$,$9$,$10填入3 × 3$的方格中,使得每行、每列、每条对角线上的三个数之和相等.

答案:
(1)如图①所示
(2)$2 + 3 + 4 = 9$,则每行、每列、每条对角线上的三个数之和均为 9,所填结果如图②所示
(3)因为 $2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 = 54$,所以三行所有数的和为 54,所以每一行的三个数之和为 18,类比
(2)中的规律,中间格应填 6,相加等于 12 的两个数对称排列,如图③所示. (答案不唯一)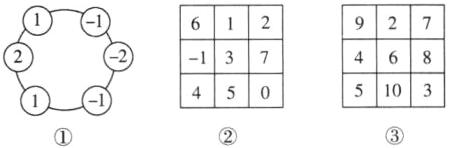
(1)如图①所示
(2)$2 + 3 + 4 = 9$,则每行、每列、每条对角线上的三个数之和均为 9,所填结果如图②所示
(3)因为 $2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 = 54$,所以三行所有数的和为 54,所以每一行的三个数之和为 18,类比
(2)中的规律,中间格应填 6,相加等于 12 的两个数对称排列,如图③所示. (答案不唯一)

查看更多完整答案,请扫码查看


