第120页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
- 第138页
- 第139页
- 第140页
- 第141页
- 第142页
- 第143页
- 第144页
- 第145页
- 第146页
- 第147页
- 第148页
- 第149页
- 第150页
15.观察与思考:我们知道1 + 2 + 3 + … + n = $\frac{n(n + 1)}{2}$,那么1^3 + 2^3 + 3^3 + … + n^3结果等于多少呢?请你仔细观察,找出下面图形与算式的关系,解决下列问题:

1^3 = 1^2;1^3 + 2^3 = 3^2;1^3 + 2^3 + 3^3 = 6^2;1^3 + 2^3 + 3^3 + 4^3 = 10^2.
(1)规律观察:1^3 + 2^3 + 3^3 + 4^3 + 5^3 =
(2)推算概括:用含n的式子表示出1^3 + 2^3 + 3^3 + … + n^3 =
(3)拓展应用:$\frac{1^3 + 2^3 + 3^3 + … + 100^3}{1 + 2 + 3 + … + 100}$ =

1^3 = 1^2;1^3 + 2^3 = 3^2;1^3 + 2^3 + 3^3 = 6^2;1^3 + 2^3 + 3^3 + 4^3 = 10^2.
(1)规律观察:1^3 + 2^3 + 3^3 + 4^3 + 5^3 =
15
^2;(2)推算概括:用含n的式子表示出1^3 + 2^3 + 3^3 + … + n^3 =
[$\frac{n(n+1)}{2}$]²
;(3)拓展应用:$\frac{1^3 + 2^3 + 3^3 + … + 100^3}{1 + 2 + 3 + … + 100}$ =
5050
.
答案:
(1)15 解析:因为1³=1²,1³+2³=(1+2)²=3²,1³+2³+3³=(1+2+3)²=6²,1³+2³+3³+4³=(1+2+3+4)²=10²,所以1³+2³+3³+4³+5³=(1+2+3+4+5)²=15²。
(2)[$\frac{n(n+1)}{2}$]² 解析:由
(1)得1³+2³+3³+…+n³=(1+2+3+…+n)²=[$\frac{n(n+1)}{2}$]²。
(3)5050 解析:$\frac{1³+2³+3³+...+100³}{1+2+3+...+100}$=$\frac{(1+2+3+...+100)²}{1+2+3+...+100}$=1+2+3+...+100=$\frac{100×(100+1)}{2}$=5050。
(1)15 解析:因为1³=1²,1³+2³=(1+2)²=3²,1³+2³+3³=(1+2+3)²=6²,1³+2³+3³+4³=(1+2+3+4)²=10²,所以1³+2³+3³+4³+5³=(1+2+3+4+5)²=15²。
(2)[$\frac{n(n+1)}{2}$]² 解析:由
(1)得1³+2³+3³+…+n³=(1+2+3+…+n)²=[$\frac{n(n+1)}{2}$]²。
(3)5050 解析:$\frac{1³+2³+3³+...+100³}{1+2+3+...+100}$=$\frac{(1+2+3+...+100)²}{1+2+3+...+100}$=1+2+3+...+100=$\frac{100×(100+1)}{2}$=5050。
16.(2025·南京期末)按图示切割正方体就可以切割出正六边形(正六边形的各顶点恰是其棱的中点),以下此正方体的平面展开图及切割线的画法正确的有
①③④
.(填序号)
答案:
①③④ 解析:对于①,将展开图重新折叠可得出原来的正方体(含切割线),符合题意;对于②,将展开图重新折叠不能得出原来的正方体(含切割线),不符合题意;对于③,将展开图重新折叠可得出原来的正方体(含切割线),符合题意;对于④,将展开图重新折叠可得出原来的正方体(含切割线),符合题意。故答案为①③④。
17.新趋势 项目式学习 (2025·龙岩期末)【综合与实践】
“好学小组”和“乐学小组”开展了“长方体纸盒的制作”实践活动.他们利用边长为a cm的正方形纸板设计成如图所示的甲、乙两种纸盒,甲种纸盒是无盖的纸盒,乙种纸盒是有盖的纸盒.
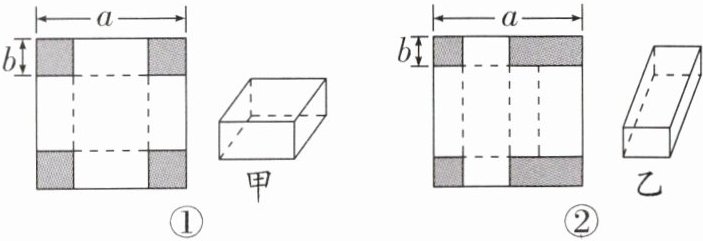
【动手操作】好学小组:根据图①方式制作一个甲种无盖的长方体盒子.方法是先在纸板四角剪去四个同样大小边长为b cm的小正方形,再沿虚线折合起来.乐学小组:根据图②方式制作一个乙种有盖的长方体纸盒.方法是先在纸板四角剪去两个同样大小边长为b cm的小正方形和两个同样大小的小长方形,再沿虚线折合起来.

【问题解决】
(1)①无盖长方体纸盒的底面积为______cm^2(用含a和b的代数式表示);
②有盖长方体纸盒的底面周长为______cm(用含a和b的代数式表示).
【拓展探究】
(2)两小组探究发现:按照上面的制作方案,甲种纸盒的体积和乙种纸盒的体积的比$\frac{V_{甲}}{V_{乙}}$与a,b取值无关.请你写出$\frac{V_{甲}}{V_{乙}}$的值,并说明理由.
【实际应用】
(3)春节临近,杭城某纸箱厂接到一笔订单,需要赶制长、宽、高分别为40cm、30cm、10cm的有盖长方体盒子若干.为了降低成本,提高效率,厂方决定购买大小合适的长方形纸板,采用乙种纸盒的制作方案,并且一张纸板制作一个纸盒.
①请分别在图③、图④虚线框内画出两种不同的设计图,并标上相应的尺寸;
②求厂方采购的长方形纸板的最小面积.
“好学小组”和“乐学小组”开展了“长方体纸盒的制作”实践活动.他们利用边长为a cm的正方形纸板设计成如图所示的甲、乙两种纸盒,甲种纸盒是无盖的纸盒,乙种纸盒是有盖的纸盒.

【动手操作】好学小组:根据图①方式制作一个甲种无盖的长方体盒子.方法是先在纸板四角剪去四个同样大小边长为b cm的小正方形,再沿虚线折合起来.乐学小组:根据图②方式制作一个乙种有盖的长方体纸盒.方法是先在纸板四角剪去两个同样大小边长为b cm的小正方形和两个同样大小的小长方形,再沿虚线折合起来.

【问题解决】
(1)①无盖长方体纸盒的底面积为______cm^2(用含a和b的代数式表示);
②有盖长方体纸盒的底面周长为______cm(用含a和b的代数式表示).
【拓展探究】
(2)两小组探究发现:按照上面的制作方案,甲种纸盒的体积和乙种纸盒的体积的比$\frac{V_{甲}}{V_{乙}}$与a,b取值无关.请你写出$\frac{V_{甲}}{V_{乙}}$的值,并说明理由.
【实际应用】
(3)春节临近,杭城某纸箱厂接到一笔订单,需要赶制长、宽、高分别为40cm、30cm、10cm的有盖长方体盒子若干.为了降低成本,提高效率,厂方决定购买大小合适的长方形纸板,采用乙种纸盒的制作方案,并且一张纸板制作一个纸盒.
①请分别在图③、图④虚线框内画出两种不同的设计图,并标上相应的尺寸;
②求厂方采购的长方形纸板的最小面积.
答案:
(1)①(a−2b)²②3(a−2b) 解析:底面长方形的宽为(a−2b)÷2=$\frac{1}{2}$(a−2b)=($\frac{1}{2}$a−b)cm,底面周长为2(a−2b+$\frac{1}{2}$a−b)=2($\frac{3}{2}$a−3b)=3(a−2b)(cm)。
(2)V甲:V乙=2:1。理由如下:依题意得V甲=(a−2b)²·b,V乙=(a−2b)·$\frac{1}{2}$(a−2b)·b=$\frac{1}{2}$(a−2b)²·b,所以$\frac{V甲}{V乙}$=$\frac{(a−2b)²·b}{\frac{1}{2}(a−2b)²·b}$=2,所以V甲:V乙=2:1。
(3)①两种不同的设计图如下: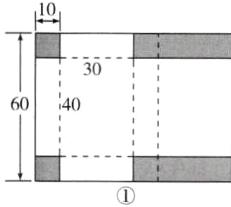
 ②图①中长方形纸板的面积为S3=60×80=4800(cm²),图②中长方形纸板的面积为S4=50×100=5000(cm²),因为4800<5000,所以厂方采购的长方形纸板的最小面积为4800cm²。
②图①中长方形纸板的面积为S3=60×80=4800(cm²),图②中长方形纸板的面积为S4=50×100=5000(cm²),因为4800<5000,所以厂方采购的长方形纸板的最小面积为4800cm²。
(1)①(a−2b)²②3(a−2b) 解析:底面长方形的宽为(a−2b)÷2=$\frac{1}{2}$(a−2b)=($\frac{1}{2}$a−b)cm,底面周长为2(a−2b+$\frac{1}{2}$a−b)=2($\frac{3}{2}$a−3b)=3(a−2b)(cm)。
(2)V甲:V乙=2:1。理由如下:依题意得V甲=(a−2b)²·b,V乙=(a−2b)·$\frac{1}{2}$(a−2b)·b=$\frac{1}{2}$(a−2b)²·b,所以$\frac{V甲}{V乙}$=$\frac{(a−2b)²·b}{\frac{1}{2}(a−2b)²·b}$=2,所以V甲:V乙=2:1。
(3)①两种不同的设计图如下:

 ②图①中长方形纸板的面积为S3=60×80=4800(cm²),图②中长方形纸板的面积为S4=50×100=5000(cm²),因为4800<5000,所以厂方采购的长方形纸板的最小面积为4800cm²。
②图①中长方形纸板的面积为S3=60×80=4800(cm²),图②中长方形纸板的面积为S4=50×100=5000(cm²),因为4800<5000,所以厂方采购的长方形纸板的最小面积为4800cm²。 查看更多完整答案,请扫码查看


