《2025年学霸题中题七年级数学上册苏科版》

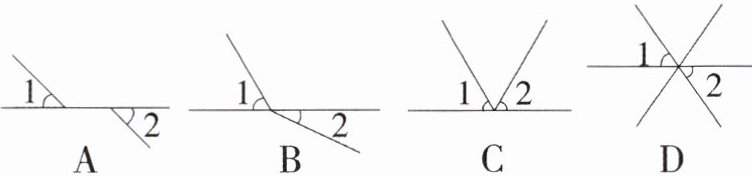
1. 教材P172练习T1变式 (2024·北京期中)下列各图中,$∠1和∠2$是对顶角的是 (D)

答案： D

2. 下列说法中正确的是 (D)
A.相等的角是对顶角
B.两条直线相交所成的两个角是对顶角
C.有公共顶点,并且相等的角是对顶角
D.对顶角的余角和补角都相等

答案： D

3. 新趋势 跨学科融合 (2025·吉安模拟)光线从空气斜射向水中时会发生折射现象,如图,长方形ABFE为盛满水的水槽,一束光线从点P射向水面上的点D,折射后照到水槽底部的点C.测得$α=40^{\circ },β=30^{\circ }$,若P,D,B三点在同一条直线上,则$∠BDC$的度数为 (D)
A.$40^{\circ }$
B.$30^{\circ }$
C.$20^{\circ }$
D.$10^{\circ }$

答案： D

4. 如图,直线a,b相交于点O,将量角器的中心与点O重合,发现表示$60^{\circ }$的点在直线a上,表示$135^{\circ }$的点在直线b上,则$∠1= $75$^{\circ }$.

答案： 75

5. (1)如图①,直线AB,CD,EF相交于点O,$∠1= 20^{\circ },∠BOC= 80^{\circ }$,则$∠2$的度数为$60^\circ$.
(2)如图②,已知直线AB和CD相交于点O,$∠COE$是直角,OF平分$∠AOE,∠COF= 24^{\circ }$,则$∠BOD$的度数为42$^{\circ }$.

答案：
(1) $60^\circ$
(2) 42

6. 如图,直线AB,CD相交于点O,OE平分$∠AOD,∠FOC= 90^{\circ },∠1= 40^{\circ }$,求$∠2和∠3$的度数.

答案： 因为 $ \angle FOC = 90^\circ $，$ \angle 1 = 40^\circ $，AB 为直线，所以 $ \angle 3 + \angle FOC + \angle 1 = 180^\circ $，所以 $ \angle 3 = 180^\circ - 90^\circ - 40^\circ = 50^\circ $。因为 $ \angle AOD $ 和 $ \angle BOC $ 为对顶角，所以 $ \angle AOD = 40^\circ + 90^\circ = 130^\circ $。因为 OE 平分 $ \angle AOD $，所以 $ \angle 2 = \frac{1}{2} \angle AOD = 65^\circ $。

7. (2024·高密月考)如图,直线AB与CD相交于点O,$∠DOE= α,∠DOF:∠AOD= 2:3$,射线OE平分$∠BOF$,则$∠BOC= $ (D)
A.$30^{\circ }$
B.$40^{\circ }$
C.$540^{\circ }-5α$
D.$540^{\circ }-6α$

答案： D 解析：设 $ \angle DOF = 2x $，则 $ \angle AOD = 3x $，所以 $ \angle AOF = 5x $，所以 $ \angle BOF = 180^\circ - 5x $。因为 OE 平分 $ \angle BOF $，所以 $ \angle FOE = \frac{1}{2} \angle BOF = \frac{1}{2}(180^\circ - 5x) = 90^\circ - \frac{5}{2}x $。因为 $ \angle DOE = \alpha $，所以 $ \angle DOF + \angle FOE = \alpha $，即 $ 2x + 90^\circ - \frac{5}{2}x = \alpha $，解得 $ x = 180^\circ - 2\alpha $。则 $ \angle AOD = 3x = 3 × (180^\circ - 2\alpha) = 540^\circ - 6\alpha $，所以 $ \angle BOC = \angle AOD = 540^\circ - 6\alpha $。故选 D。

8. (2024·深圳期中)如图,直线AB,CD相交于点O,$∠AOE= 90^{\circ },∠DOF= 90^{\circ }$,OB平分$∠DOG$,给出下列结论:①当$∠AOF= 60^{\circ }$时,$∠DOE= 60^{\circ }$;②与$∠BOD$相等的角有三个;③OD为$∠EOG$的平分线;④$∠COG= 180^{\circ }-2∠EOF$.其中正确的结论有 (C)

A.1个
B.2个
C.3个
D.4个

答案： C 解析：$ \angle AOF + \angle EOF = \angle DOE + \angle EOF = 90^\circ $，因此 $ \angle AOF = \angle DOE $，当 $ \angle AOF = 60^\circ $ 时，$ \angle DOE = 60^\circ $，正确，故 ① 符合题意；OB 平分 $ \angle GOD $，因此 $ \angle GOD = 2 \angle BOD $，而 $ \angle DOE = 90^\circ - \angle BOD $，所以 $ \angle DOE $ 不一定等于 $ \angle GOD $，因此 OD 不一定是 $ \angle EOG $ 的平分线，故 ③ 不符合题意；$ \angle EOF + \angle EOD = \angle BOD + \angle EOD = 90^\circ $，因此 $ \angle EOF = \angle BOD $，由 OB 平分 $ \angle GOD $ 得到 $ \angle GOB = \angle BOD $，又 $ \angle AOC = \angle BOD $，因此与 $ \angle BOD $ 相等的角有三个，正确，故 ② 符合题意；$ \angle COG = \angle AOB - \angle AOC - \angle GOB = \angle AOB - 2 \angle EOF = 180^\circ - 2 \angle EOF $，正确，故 ④ 符合题意。其中正确的结论有 3 个。故选 C。