《2025年学霸题中题七年级数学上册苏科版》

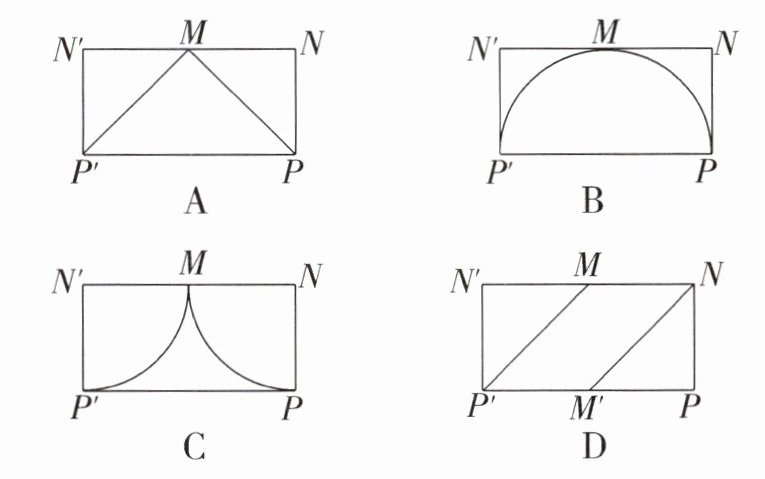
9.(2025·扬州期末)如图,已知MN是圆柱底面的直径,NP是圆柱的高,在圆柱的侧面上,过点M,P嵌有一圈路径最短的金属丝,现将圆柱侧面沿NP剪开,所得的侧面展开图是 (A)

答案： A 解析：因为圆柱侧面展开图是长方形，且MP是最短路径，故MP展开应该是两条有交点的线段，故选A。

10.如图是一个长方体纸盒的表面展开图,纸片厚度忽略不计,由图中数据,可得这个纸盒的容积为6.

答案： 6 解析：3−1=2，5−2=3，所以长方体的长、宽、高分别为3，2，1，1×2×3=6，则这个纸盒的容积为6。

11.把图①所示正方体的表面展开图围成正方体(文字露在外面),再将这个正方体按照图②依次翻滚到第1格、第2格、第3格、第4格,此时正方体朝上一面的文字为富.

答案： 富 解析：由题图①可得，“富”和“文”相对；“强”和“主”相对；“民”和“明”相对；由题图②可得，正方体从题图②的位置依次翻滚到第4格时，“文”在下面，则这时正方体朝上一面的文字是“富”。

12.(2024·南京校级月考)如图,图①为一个长方体,AD = AB = 8,AE = 5,M为所在棱的中点,图②为图①的表面展开图,则图②中△ABM的面积为$______cm^2.$

答案：
16或68 解析：由长方体的展开图可分类讨论：①当点M的位置如图①，且为所在线段EF中点时，连接AM，BM，所以EM=$\frac{1}{2}$EF=$\frac{1}{2}$AD=4cm，所以S△ABM=$\frac{1}{2}$AB·EM=$\frac{1}{2}$×8×4=16(cm²)；②当点M的位置如图②，且为线段PQ中点时，连接BM，所以AM=AD+DP+PM=AD+AE+AD=8+5+4=17(cm)，所以S△ABM=$\frac{1}{2}$AB·AM=$\frac{1}{2}$×8×17=68(cm²)。综上，△ABM的面积为16cm²或68cm²。

13.如图,已知一个正方体的六个面上分别写着六个连续的整数,且每两个相对面上的数的和都相等,图中所能看到的数是16,19和20.
(1)画出这个正方体的表面展开图(只需画出一个即可);
(2)求这6个整数的和.

答案：

(1)答案不唯一，如图。
(2)因为正方体的六个面上是六个连续的整数，能看到的数是16，19和20，所以可能的情况有①15，16，17，18，19，20；②16，17，18，19，20，21。由于题目要求每两个相对面上的数的和都相等，当和相等且为35时，16的对面应该是19，与题图不符，所以第一种情况不可能，故可能的情况只有第二种。所以6个整数的和为16+17+18+19+20+21=111。

14.已知三棱柱如图①所示,其底面边长都是2cm,侧棱长为8cm.
(1)若将它的表面沿某些棱剪开,展成一个平面图形,在图②的四幅展开图中,可能是该三棱柱表面展开图的有______(填序号);
(2)图③是已知三棱柱的一种表面展开图,请你求出图③的外围周长;
(3)请你画出一种该已知三棱柱的表面展开图,使其外围周长最大,并直接写出它的外围周长.

答案：

(1)AD
(2)题图③的外围周长为2×6+8×4=44(cm)。
(3)图形画法不唯一，例如：其外围周长为2×4+8×6=56(cm)。