《2025年学霸题中题七年级数学上册苏科版》

11. 平方等于它本身的数是0,1,立方等于它本身的数是-1,0,1,平方等于它相反数的数是0,-1,立方等于它相反数的数是0.

答案： 0,1 -1,0,1 0,-1 0

12. 观察下列算式: (1) $3^1= 3$, (2) $3^2= 9$, (3) $3^3= 27$, (4) $3^4= 81$, (5) $3^5= 243$, (6) $3^6= 729$, (7) $3^7= $ 2187 , (8) $3^8= 6561, …$. 根据算式中的规律, 你认为 $3^{100}$ 的个位数字是____1.

答案： 1 解析:观察个位数字,易知 3 的 1,2,3,4,5,6,7,8…次方的个位数字以 3,9,7,1 四个数字为一组循环出现,又 100÷4 = 25,所以 3¹⁰⁰ 的个位数字与 3⁴ 的个位数字相同,是 1.

13. 新题型 新定义 (2024·内江校级月考) 定义:如果$a^x= N(a＞0$, 且$a \neq 1)$, 那么 $x$ 叫作以 $a$ 为底 $N$ 的对数, 记作 $x= \log _a N$. 例如: 因为 $7^2= 49$, 所以 $\log _7 49= 2$; 因为 $5^3= 125$, 所以 $\log _5 125= 3$. 下列说法: (1) $\log _6 6= 36$; (2) $\log _3 81= $ 4; (3)若 $\log _4(a+14)= 2$, 则 $a= 2$; (4) $\log _2 64= $ $\log _2 32+\log _2 2$. 正确的有____②③④(填序号).

答案： ②③④ 解析:因为 6¹ = 6,所以 log₆6 = 1. 故①错误.因为 3⁴ = 81,所以 log₃81 = 4. 故②正确.因为 log₄(a + 14) = 2,所以 a + 14 = 4²,所以 a = 2. 故③正确.因为 log₂64 = 6,log₂32 = 5,log₂2 = 1. 故④正确.故答案为②③④.

14. 阅读下列各式: $(a × b)^2= a^2 × b^2,(a × b)^3= a^3 ×$ $b^3,(a × b)^4= a^4 × b^4,(a × b)^5= a^5 × b^5 … …$
回答下列问题:
(1) 猜想: $(a × b)^n= $$aⁿ×bⁿ$.
(2) 请用我们学过的知识说明上式成立的理由.
$(a× b)ⁿ = \underbrace{(a× b)×(a× b)×\cdots×(a× b)}_{n个(a× b)相乘} = a×b×a×b×…×a×b = \underbrace{(a× a×\cdots× a)}_{n个a相乘}×\underbrace{(b× b×\cdots× b)}_{n个b相乘} = aⁿ×bⁿ.$
(3) 请计算:
(1) $\left(-\frac{1}{4}\right)^{1000} × 4^{1000}$;
$\left(-\frac{1}{4}\right)^{1000} × 4^{1000} = \left(-\frac{1}{4}×4\right)^{1000} = 1.$
(2) $(-0.125)^{2025} × 2^{2024} × 4^{2023}$.
$(-0.125)^{2025} × 2^{2024} × 4^{2023} = \left(-\frac{1}{8}\right)^2×\left(-\frac{1}{8}\right)^{2023}×2×2^{2023}×4^{2023} = \frac{1}{64}×2×\left(-\frac{1}{8}×2×4\right)^{2023} = \frac{1}{32}×(-1) = -\frac{1}{32}.$

答案：
(1) aⁿ×bⁿ
(2) (a×b)ⁿ = $\underbrace{(a× b)×(a× b)×\cdots×(a× b)}_{n个(a× b)相乘}$ = a×b×a×b×…×a×b = $\underbrace{(a× a×\cdots× a)}_{n个a相乘}$×$\underbrace{(b× b×\cdots× b)}_{n个b相乘}$ = aⁿ×bⁿ.
(3) ① (-$\frac{1}{4}$)¹⁰⁰⁰×4¹⁰⁰⁰ = (-$\frac{1}{4}$×4)¹⁰⁰⁰ = 1.② (-0.125)²⁰²⁵×2²⁰²⁴×4²⁰²³ = (-$\frac{1}{8}$)²×(-$\frac{1}{8}$)²⁰²³×2×2²⁰²³×4²⁰²³ = $\frac{1}{64}$×2×(-$\frac{1}{8}$×2×4)²⁰²³ = $\frac{1}{32}$×(-1) = -$\frac{1}{32}$.

15. (2025·深圳期中) 在一次综合实践活动课上, 张老师给每位同学各发了一张正方形纸片, 请同学们思考如何通过折纸的方法求出 $\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+…+\frac{1}{2^6}$ 的值.
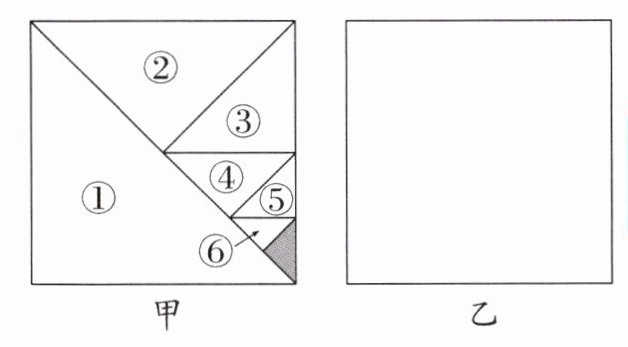
【操作探究】“乘风”小组的同学经过一番思考和讨论交流后, 进行了如下操作: 如图甲, 将一个边长为 1 的正方形纸片分割成 7 个部分, 第(1)部分是边长为 1 的正方形纸片面积的一半, 第(2)部分是第(1)部分面积的一半, 第(3)部分是第(2)部分面积的一半……依次类推, 则图甲中空白部分的面积为 $\frac{1}{2}+\frac{1}{4}+$ $\frac{1}{8}+…+\frac{1}{2^6}$.
“破浪”小组是这样思考的: 设 $S= \frac{1}{2}+\frac{1}{4}+$ $\frac{1}{8}+…+\frac{1}{2^6}$,
将等式两边同时乘 $\frac{1}{2}$ 得 $\frac{1}{2} S= \frac{1}{4}+\frac{1}{8}+…+$ $\frac{1}{2^6}+\frac{1}{2^7}$,
将上式减去下式得 $\frac{1}{2} S= \frac{1}{2}-\frac{1}{2^7}$, 即 $S= 1-\frac{1}{2^6}= $ $\frac{63}{64}$, 即 $\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+…+\frac{1}{2^6}= \frac{63}{64}$.
甲
乙

【过程思考】
(1) 图甲中阴影部分的面积是____, $\frac{1}{2}+$ $\frac{1}{4}+\frac{1}{8}+…+\frac{1}{2^7}= $____.
(2) 请你利用图乙, 再设计能求 $\frac{1}{2}+\frac{1}{4}+$ $\frac{1}{8}+…+\frac{1}{2^6}$ 的值的几何图形. (只画出图形即可)
(3) 根据以上规律, 计算:
(1) $\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+…+\frac{1}{2^n}= $____; ( $n$ 为正整数)
(2) $2+4+8+16+…+2^n= $____. ( $n$ 为正整数)

答案：

(1) $\frac{1}{64}$ $\frac{127}{128}$ 解析:由题知,正方形每次被分割的部分是前一部分面积的一半,所以题图中阴影部分的面积与第⑥部分的面积相等.又因为第①部分的面积为 $\frac{1}{2}$ = $\frac{1}{2¹}$,第②部分的面积为 $\frac{1}{2}$×$\frac{1}{2}$ = $\frac{1}{4}$ = $\frac{1}{2²}$,第③部分的面积为 $\frac{1}{2}$×$\frac{1}{2}$×$\frac{1}{2}$ = $\frac{1}{8}$ = $\frac{1}{2³}$……依次类推,第 n 部分的面积为 $\frac{1}{2ⁿ}$. 当 n = 6 时,$\frac{1}{2ⁿ}$ = $\frac{1}{2⁶}$ = $\frac{1}{64}$,所以阴影部分的面积为 $\frac{1}{64}$.因为 $\frac{1}{2}$ + $\frac{1}{2²}$ + $\frac{1}{2³}$ + … + $\frac{1}{2⁷}$ + $\frac{1}{2⁷}$ = 1,所以 $\frac{1}{2}$ + $\frac{1}{4}$ + $\frac{1}{8}$ + … + $\frac{1}{2⁷}$ = 1 - $\frac{1}{2⁷}$ = $\frac{127}{128}$.
(2) 如图所示(标序号部分)即为求 $\frac{1}{2}$ + $\frac{1}{4}$ + $\frac{1}{8}$ + … + $\frac{1}{2⁶}$ 的值的几何图形.(所画图形合理即可)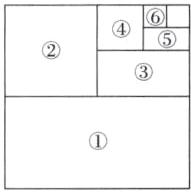
(3) ① 1 - $\frac{1}{2ⁿ}$ 解析:根据前面的分析可知 $\frac{1}{2}$ + $\frac{1}{4}$ + $\frac{1}{8}$ + … + $\frac{1}{2ⁿ}$ = 1 - $\frac{1}{2ⁿ}$.② 2ⁿ⁺¹ - 2 解析:令 S = 2 + 4 + 8 + 16 + … + 2ⁿ ①,将等式两边同时乘 2 得 2S = 4 + 8 + 16 + … + 2ⁿ + 2ⁿ⁺¹ ②,将②式减去①式得 S = 2ⁿ⁺¹ - 2,即 2 + 4 + 8 + 16 + … + 2ⁿ = 2ⁿ⁺¹ - 2.