《2025年学霸题中题七年级数学上册苏科版》

11. 观察下面一系列等式：
①$2^2 - 2^1 = 4 - 2 = 2^1$；
②$2^3 - 2^2 = 8 - 4 = 2^2$；
③$2^4 - 2^3 = 16 - 8 = 2^3$；
④______；
…
(1)请按这个顺序仿照前面的等式写出第④个等式：$2^{5}-2^{4}=32 - 16 = 2^{4}$；
(2)根据你上面所发现的规律,用含字母n的式子表示第ⓝ个等式：$2^{n + 1}-2^{n}=2^{n}$，并说明这个规律的正确性；
(3)请利用上述规律计算：$2^1 + 2^2 + 2^3 + … + 2^{100}$。
根据规律，$2^{1}+2^{2}+2^{3}+\cdots+2^{100}=(2^{2}-2^{1})+(2^{3}-2^{2})+(2^{4}-2^{3})+\cdots+(2^{101}-2^{100})=2^{2}-2^{1}+2^{3}-2^{2}+2^{4}-2^{3}+\cdots+2^{101}-2^{100}=-2^{1}+2^{101}=2^{101}-2$。

答案：
(1) $2^{5}-2^{4}=32 - 16 = 2^{4}$
(2) $2^{n + 1}-2^{n}=2^{n}$ 说明：因为 $2^{n + 1}-2^{n}=\underbrace{2×2×2×\cdots×2}_{(n + 1)\text{个}2}-\underbrace{2×2×2×\cdots×2}_{n\text{个}2}=\underbrace{2×2×2×\cdots×2}_{n\text{个}2}×(2 - 1)=\underbrace{2×2×2×\cdots×2}_{n\text{个}2}=2^{n}$，所以 $2^{n + 1}-2^{n}=2^{n}$.
(3) 根据规律，$2^{1}+2^{2}+2^{3}+\cdots+2^{100}=(2^{2}-2^{1})+(2^{3}-2^{2})+(2^{4}-2^{3})+\cdots+(2^{101}-2^{100})=2^{2}-2^{1}+2^{3}-2^{2}+2^{4}-2^{3}+\cdots+2^{101}-2^{100}=-2^{1}+2^{101}=2^{101}-2$.

12. 新趋势 数学文化 分形的概念是由数学家本华·曼德博提出的。如图是分形的一种,第1个图案有2个三角形；第2个图案有4个三角形；第3个图案有8个三角形；第4个图案有16个三角形；…。下列数据中是按此规律分形得到的三角形的个数是(D)
A.126

B.513
C.980
D.1024

答案： D

13. 新考法 (2025·淄博期中)生物课题小组对附着在物体表面的三个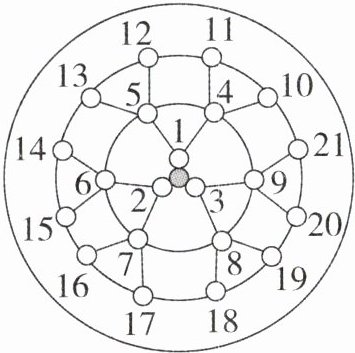微生物(课题组成员把它们分别标号为1,2,3)的生长情况进行观察记录,这三个微生物第1天各自一分为二产生新的微生物(依次标号为4,5,6,7,8,9),接下去每天都按照这样的规律变化,即每个微生物一分为二,形成新的微生物(课题组成员用如图所示的图形进行形象地记录),那么标号为100的微生物会出现在(B)
A.第4天
B.第5天
C.第6天
D.第7天

答案： B 解析：第一天产生新的微生物有 6 个标号，第二天产生新的微生物有 12 个标号，以此类推，第三天、第四天、第五天……产生新的微生物分别有 24 个，48 个，96 个，所以标号为 100 的微生物会出现在第 5 天. 故选 B.

14. (2025·南京校级月考)平移小平行四边形◇可以得到美丽的“中国结”图案,下面四个图案是由小平行四边形◇平移后得到的类似“中国结”的图案,按图中规律,在第n个图案中,小平行四边形◇的个数是______$2n^{2}$。

答案： $2n^{2}$ 解析：第一个图形有 $2×1^{2}=2$（个）小平行四边形；第二个图形有 $2×2^{2}=8$（个）小平行四边形；第三个图形有 $2×3^{2}=18$（个）小平行四边形……第 $n$ 个图形有 $2n^{2}$ 个小平行四边形.

15. (2025·无锡期末)用若干黑白两色的正方形按如图所示的方式摆放,依此规律,第n个图形中小正方形的总个数是$(n + 1)^{2}$；若第n个图形中白色正方形的个数记为$S_n$,计算：$(1 + \frac{1}{S_1})×(1 + \frac{1}{S_2})×(1 + \frac{1}{S_3})×…×(1 + \frac{1}{S_{20}}) = $$\frac{21}{11}$。

答案： $(n + 1)^{2}$ $\frac{21}{11}$ 解析：第 1 个图形：小正方形的总个数是 $(1 + 1)^{2}=4$；第 2 个图形：小正方形的总个数是 $(2 + 1)^{2}=9$；第 3 个图形：小正方形的总个数是 $(3 + 1)^{2}=16$；第 4 个图形：小正方形的总个数是 $(4 + 1)^{2}=25\cdots\cdots$ 以此类推，第 $n$ 个图形中小正方形的总个数是 $(n + 1)^{2}$；因为第 $n$ 个图形中白色正方形的个数记为 $S_{n}$，所以 $S_{1}=(1 + 1)^{2}-1 = 3$，$S_{2}=(2 + 1)^{2}-1 = 8$，$S_{3}=(3 + 1)^{2}-1 = 15$，$S_{4}=(4 + 1)^{2}-1 = 24\cdots\cdots$ 以此类推：第 $n$ 个图形中白色正方形的个数记为 $S_{n}=(n + 1)^{2}-1$，所以 $(1+\frac{1}{S_{1}})×(1+\frac{1}{S_{2}})×(1+\frac{1}{S_{3}})×\cdots×(1+\frac{1}{S_{20}})=(1+\frac{1}{3})×(1+\frac{1}{8})×(1+\frac{1}{15})×\cdots×(1+\frac{1}{440})=\frac{4}{3}×\frac{9}{8}×\frac{16}{15}×\frac{25}{24}×\cdots×\frac{441}{440}=\frac{3}{2}×\frac{16}{15}×\frac{25}{24}×\cdots×\frac{441}{440}=\frac{3}{2}×\frac{2}{3}×\frac{5}{3}×\cdots×\frac{441}{440}=\frac{5}{3}×\frac{36}{35}×\frac{49}{48}×\cdots×\frac{441}{440}=\frac{5}{3}×\frac{3}{5}×\frac{7}{4}×\cdots×\frac{441}{440}=\frac{7}{4}×\frac{64}{63}×\frac{81}{80}×\cdots×\frac{400}{399}×\frac{441}{440}=\frac{7}{4}×\frac{4}{7}×\frac{9}{5}×\cdots×\frac{21}{11}=\frac{21}{11}$.