《2025年一本同步训练八年级数学上册人教版重庆专版》

5.如图，地面上有$A$，$B$，$C$三个洞口，老鼠可能从任意一个洞口跑出，小猫为能同时且最省力地顾及到三个洞口，尽快抓住老鼠，小猫应该蹲在（D）

A.$\triangle ABC$的三条角平分线的交点处
B.$\triangle ABC$的三条中线的交点处
C.$\triangle ABC$的三条高的交点处
D.$\triangle ABC$的三条边的垂直平分线的交点处

答案： D

6.如图，在$\triangle ABC$中，$DE$是$AC$的垂直平分线，交$BC$于点$D$，交$AC$于点$E$，$\triangle ABD$的周长为$15\mathrm{c}\mathrm{m}$，$AC=5\mathrm{c}\mathrm{m}$，则$\triangle ABC$的周长为20cm.

答案： $20\mathrm{cm}$

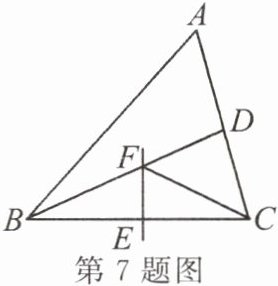
7.如图，在$\triangle ABC$中，$BD$平分$\angle ABC$，$BC$的垂直平分线交$BC$于点$E$，交$BD$于点$F$，连接$CF$.若$\angle A=60^{\circ}$，$\angle ACF=48^{\circ}$，则$\angle ABC$的度数为$48^{\circ}$.

答案： $48^{\circ}$

8.(2025·重庆八中期中)如图，在$\triangle ABC$中，$BD$平分$\angle ABC$交$AC$于点$D$.

(1)尺规作图：作线段$BD$的垂直平分线$EF$，垂足为$M$，分别交$AB$，$BC$于点$E$，$F$，连接$DE$(保留作图痕迹，不写作法).
(2)在(1)的条件下，求证：$BF=DE$.请将下面的证明过程补充完整.
证明：$\because BD$平分$\angle ABC$，
$\therefore$①$\angle ABD=\angle CBD$.
$\because EF$是线段$BD$的垂直平分线，
$\therefore \angle BME=\angle BMF=90^{\circ}$.
在$\triangle BEM$和$\triangle BFM$中，
$\left\{\begin{array}{l}\angle ABD=\angle CBD,\\ ②$BM=BM$,\\ \angle BME=\angle BMF,\end{array}\right.$
$\therefore \triangle BEM≌\triangle BFM$（③ASA），
$\therefore$④$BE=BF$.
$\because EF$是线段$BD$的垂直平分线，
$\therefore$⑤$BE=DE$，
$\therefore BF=DE$.

答案：
(1)略
(2)①$∠ABD=∠CBD$ ②$BM=BM$ ③ASA ④$BE=BF$ ⑤$BE=DE$

9.如图，在$\triangle ABC$中，$BC=12$，$\angle BAC=100^{\circ}$，$AB$的垂直平分线交$BC$于点$E$，交$AB$于点$D$，$AC$的垂直平分线交$BC$于点$N$，交$AC$于点$M$，连接$AE$，$AN$.
(1)求$\triangle AEN$的周长；12
(2)求$\angle EAN$的度数；20°
(3)如果$DE$与$MN$交于点$P$，猜想$\triangle PBC$的形状.$\triangle PBC$是等腰三角形

答案：
(1)12
(2)$20^{\circ}$
(3)$\triangle PBC$是等腰三角形