《2025年一本同步训练八年级数学上册人教版重庆专版》

10. 如图,等边三角形 ABC 的边长为 4 cm,D,E 分别是 AB,AC 上的点,将四边形 DBCE 沿直线 DE 折叠,点 B,C 分别落在点$B',C'$处,且都在$\triangle ABC$的外部,则阴影部分图形的周长为12cm.
[变式] 三角形→正方形
如图,已知正方形 ABCD 的面积为 25,将正方形 ABCD 沿直线 EF 折叠,则图中 4 个阴影三角形的周长之和为20.

答案： 12 【变式】20

11. (2025·重庆礼嘉中学期中)在几何学习中,遇到这样一个题目:“如图,在四边形 ABCD 中,$AB＞AD$. 若 AC 平分$∠BAD,BC=CD$,求证:$∠B+∠ADC=180^{\circ }$.”结合学过的知识,可以先过点 C 分别作出 AB,AD 的垂线,将其转化为证明三角形全等,然后结合补角的知识使问题得到解决. 请根据上述的思路,完成下面的作图与填空.

(1) 尺规作图:用直尺和圆规,过点 C 作 AD 的垂线,交 AD 的延长线于点 F(只保留作图痕迹);
(2) 证明:$\because CE⊥AB,CF⊥AD,$
$\therefore ∠CEB=∠CFD=90^{\circ }.$
$\because AC$平分$∠BAD,CE⊥AB,CF⊥AD,$
$\therefore$①______CE = CF.
在$Rt\triangle CEB$和$Rt\triangle CFD$中,
$\left\{\begin{array}{l} BC=DC,\\ \textcircled{2}\_\_\_\_\_\_\_\_CE = CF, \end{array}\right.$
$\therefore Rt\triangle CEB\cong Rt\triangle CFD(HL),$
$\therefore$③______∠B = ∠CDF.
$\because ∠CDF+∠ADC=180^{\circ },$
$\therefore ∠B+$④______∠ADC$=180^{\circ }.$

答案：
(1) 略
(2) ① $ CE = CF $ ② $ CE = CF $ ③ $ ∠B = ∠CDF $ ④ $ ∠ADC $

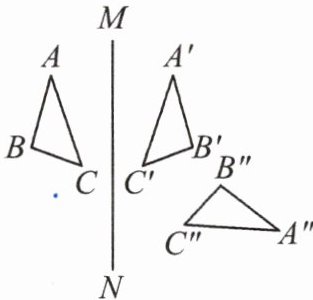
12. 如图,$\triangle ABC$和$\triangle A'B'C'$关于直线 MN 对称,$\triangle A'B'C'$和$\triangle A''B''C''$关于直线 EF 对称.
(1) 作出直线 EF(要求:保留作图痕迹,不写作法);
(2) 直线 MN 与 EF 相交于点 O,试探究$∠BOB''$与直线 MN,EF 所夹锐角α之间的数量关系.$∠BOB'' = 2α$

答案：
(1) 略
(2) $ ∠BOB'' = 2α $

13. 城中村 A,B 与两条公路$l_{1},l_{2}$的位置如图所示,因城市拆迁安置需要,在 C 处新建安置小区,要求安置小区到城中村 A,B 的距离必须相等,到两条公路$l_{1},l_{2}$的距离也必须相等,那么点 C 应选在何处? 请用尺规作图,找出所有符合条件的点 C. (不写作法,只保留作图痕迹)

作出$∠l_{1}Ol_{2}$（$O$为$l_{1}$与$l_{2}$交点）的角平分线和线段$AB$的垂直平分线，它们的交点$C_{1}$、$C_{2}$即为所求的点（作图痕迹略）

答案： 【解析】：
1. 首先，作$∠l_{1}Ol_{2}$（$O$为$l_{1}$与$l_{2}$的交点）的角平分线$OC_{1}$和$OC_{2}$（因为到两条直线$l_{1},l_{2}$距离相等的点在这两条直线所夹角的平分线上）。
2. 然后，作线段$AB$的垂直平分线$MN$（因为到$A$、$B$两点距离相等的点在线段$AB$的垂直平分线上）。
3. 最后，$OC_{1}$与$MN$的交点$C_{1}$，$OC_{2}$与$MN$的交点$C_{2}$就是符合条件的点（根据角平分线的性质和线段垂直平分线的性质，$C_{1}$、$C_{2}$既满足到$A$、$B$距离相等，又满足到$l_{1},l_{2}$距离相等）。
【答案】：作出$∠l_{1}Ol_{2}$（$O$为$l_{1}$与$l_{2}$交点）的角平分线和线段$AB$的垂直平分线，它们的交点$C_{1}$、$C_{2}$即为所求的点（作图痕迹略）。