《2025年名校课堂九年级数学上册北师大版》

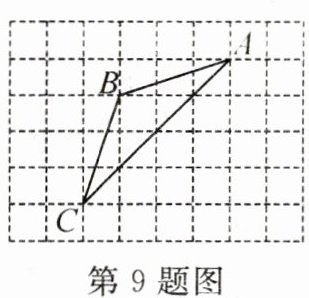
9. 如图,在正方形网格中,如果把三角形ABC的顶点C先向右平移3格,再向上平移1格得到点C',连接CC',AC',则四边形ABCC'是菱形.

答案： 菱形

10. (2024·广西改编)如图,两张宽度均为3cm的纸条交叉叠放在一起,交叉形成的锐角为60°,则重合部分构成的四边形ABCD的周长为$8\sqrt{3}$cm,面积为$6\sqrt{3}$$cm^2.$

答案： $8\sqrt{3}$ $6\sqrt{3}$

11. 如图,在▱ABCD中,点E,F分别在边BC,AD上,AC与EF交于点O,且EF垂直平分AC,连接AE,CF.
(1)求证：四边形AECF是菱形.

证明：∵四边形$ABCD$是平行四边形，∴$AD// BC$．∴$∠OAF = ∠OCE$．∵$EF$垂直平分$AC$，∴$EF⊥AC$，$OA = OC$．在$\triangle AOF$和$\triangle COE$中，$\left\{\begin{array}{l}∠OAF = ∠OCE,\\OA = OC,\\∠AOF = ∠COE,\end{array}\right.$∴$\triangle AOF≌\triangle COE$(ASA)．∴$OE = OF$．∵$OA = OC$，∴四边形$AECF$是平行四边形．又∵$EF⊥AC$，∴平行四边形$AECF$是菱形．
(2)若AC⊥AB,∠B= 30°,AE= 12,求四边形AECF的面积.72√3

答案： 解：
(1)证明：
∵四边形$ABCD$是平行四边形，
∴$AD// BC$．
∴$∠OAF = ∠OCE$．
∵$EF$垂直平分$AC$，
∴$EF⊥AC$，$OA = OC$．在$\triangle AOF$和$\triangle COE$中，$\left\{\begin{array}{l}∠OAF = ∠OCE,\\OA = OC,\\∠AOF = ∠COE,\end{array}\right.$
∴$\triangle AOF≌\triangle COE(ASA)$．
∴$OE = OF$．
∵$OA = OC$，
∴四边形$AECF$是平行四边形．又
∵$EF⊥AC$，
∴平行四边形$AECF$是菱形．
(2)由
(1)可知，$OE = OF$，四边形$AECF$是菱形，
∴$CE = AE = 12$．
∵$AC⊥AB$，$EF⊥AC$，
∴$∠COE = 90^{\circ}$，$EF// AB$．
∴$∠CEO = ∠B = 30^{\circ}$．
∴$OC=\frac{1}{2}CE = 6$．
∴$AC = 2OC = 12$，$OE=\sqrt{CE^{2}-OC^{2}}=\sqrt{12^{2}-6^{2}} = 6\sqrt{3}$．
∴$EF = 2OE = 12\sqrt{3}$．
∴$S_{菱形AECF}=\frac{1}{2}AC\cdot EF=\frac{1}{2}\times12\times12\sqrt{3}=72\sqrt{3}$．

12. 如图,菱形ABCD的两条对角线的长分别为10和24,M是边AB上的动点,P是对角线AC上的一个动点,则PM+PB的最小值是

$\frac{120}{13}$.

答案： $\frac{120}{13}$

我们已经知道：菱形的面积等于两条对角线乘积的一半,那么,如果是对角线互相垂直的任意一个四边形,还有这样的结论吗？
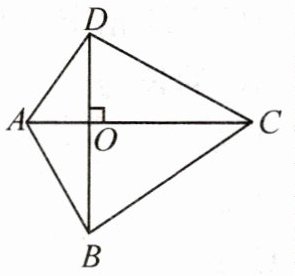
如图,四边形ABCD的对角线AC,BD互相垂直,垂足为O.若BD的长为15,AC的长为20,求四边形ABCD的面积.(请写出求解过程)
结论：对角线互相垂直的四边形的面积等于两条对角线乘积的一半.

解：$S_{四边形ABCD}=S_{\triangle ADC}+S_{\triangle BAC}=\frac{1}{2}AC\cdot OD+\frac{1}{2}AC\cdot OB=\frac{1}{2}AC\cdot(OD + OB)=\frac{1}{2}AC\cdot BD=\frac{1}{2}×20×15 = 150$．

答案： 解：$S_{四边形ABCD}=S_{\triangle ADC}+S_{\triangle BAC}=\frac{1}{2}AC\cdot OD+\frac{1}{2}AC\cdot OB=\frac{1}{2}AC\cdot(OD + OB)=\frac{1}{2}AC\cdot BD=\frac{1}{2}\times20\times15 = 150$． 两条对角线乘积的一半