第78页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
1. 在同一时刻,物体的高度与它在阳光下的影长成正比. 在某一时刻,有人测得一根高为1.8m的竹竿的影长为3m,某一幢高楼的影长为60m,那么这幢高楼的高度是 (
A. 18m
B. 20m
C. 30m
D. 36m
D
)A. 18m
B. 20m
C. 30m
D. 36m
答案:
D
2. 如图,把一根长为4.5m的竹竿AB斜靠在石坝旁,量出竿长1m处离地面的高度为0.6m,则石坝的高度为 (
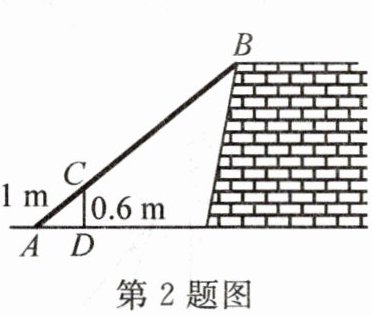
A. 2.7m
B. 3.6m
C. 2.8m
D. 2.1m
A
)
A. 2.7m
B. 3.6m
C. 2.8m
D. 2.1m
答案:
A
3. 九年级(1)班课外活动小组利用标杆测量学校旗杆的高度,如图所示,标杆高度CD= 3m,标杆与旗杆的水平距离BD= 15m,人的眼睛与地面的高度EF= 1.6m,人与标杆CD的水平距离DF= 2m,E,C,A三点共线,则旗杆AB的高度为
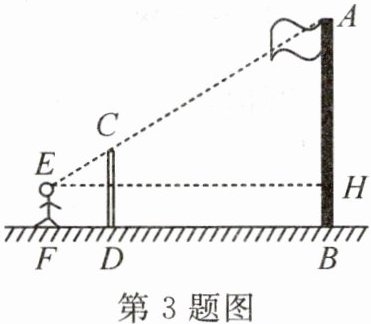
13.5
m.
答案:
13.5
4. 如图,为了测量山的高度,小明在山前的平地上竖一根已知长度的木棒O'B',测出木棒的影长A'B'与山的影长AB,即可近似求出山的高度OB. 如果O'B'= 1m,A'B'= 2m,AB= 270m,求山的高度OB.
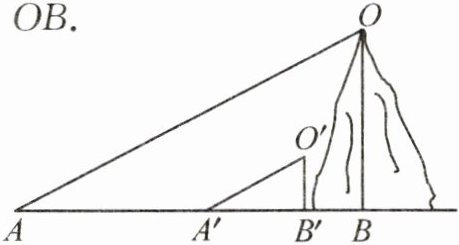
解:由题易知 $ OA // O'A' $,$\therefore \angle OAB = \angle O'A'B' $。$\because OB \perp AB$,$O'B' \perp A'B' $,$\therefore \angle ABO = \angle A'B'O' = 90^\circ $。$\therefore \triangle OAB \backsim \triangle O'A'B' $。$\therefore \frac{OB}{O'B'} = \frac{AB}{A'B'} $,即 $\frac{OB}{1} = \frac{270}{2} $。$\therefore OB = $

解:由题易知 $ OA // O'A' $,$\therefore \angle OAB = \angle O'A'B' $。$\because OB \perp AB$,$O'B' \perp A'B' $,$\therefore \angle ABO = \angle A'B'O' = 90^\circ $。$\therefore \triangle OAB \backsim \triangle O'A'B' $。$\therefore \frac{OB}{O'B'} = \frac{AB}{A'B'} $,即 $\frac{OB}{1} = \frac{270}{2} $。$\therefore OB = $
135
。答:山的高度 $ OB $ 为 135 m。
答案:
解:由题易知 $ OA // O'A' $,$\therefore \angle OAB = \angle O'A'B' $。$\because OB \perp AB$,$O'B' \perp A'B' $,$\therefore \angle ABO = \angle A'B'O' = 90^\circ $。$\therefore \triangle OAB \backsim \triangle O'A'B' $。$\therefore \frac{OB}{O'B'} = \frac{AB}{A'B'} $,即 $\frac{OB}{1} = \frac{270}{2} $。$\therefore OB = 135 $。答:山的高度 $ OB $ 为 135 m。
5. 新考向 地域文化 郑州二七纪念塔作为郑州的城市地标,坐落在距离郑州火车站不远的二七广场,共14层,为仿古联体双塔,是中国最年轻的全国重点文物保护单位. 某数学活动小组欲测量其高度. 如图,组员在点B处放置一个平面镜,站在A处恰好能从平面镜中看到塔的顶端D,分别测出:组员到平面镜距离AB= 2m,平面镜到塔底部中心的距离BC= 84m,组员眼睛到地面距离AE= 1.5m,且AE⊥AC,CD⊥AC,点A,B,C在一条水平线上. 请据此求出二七纪念塔的高度CD.
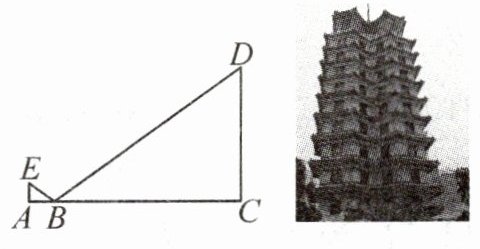
解:根据题意,得 $\angle EBA = \angle DBC $。$\because EA \perp AC$,$DC \perp AC $,$\therefore \angle EAB = \angle DCB = 90^\circ $。$\therefore \triangle ABE \backsim \triangle CBD $。$\therefore \frac{AE}{CD} = \frac{AB}{CB} $。$\because AB = 2 \text{ m}$,$BC = 84 \text{ m}$,$AE = 1.5 \text{ m} $,$\therefore \frac{1.5}{CD} = \frac{2}{84} $,解得 $ CD = $

解:根据题意,得 $\angle EBA = \angle DBC $。$\because EA \perp AC$,$DC \perp AC $,$\therefore \angle EAB = \angle DCB = 90^\circ $。$\therefore \triangle ABE \backsim \triangle CBD $。$\therefore \frac{AE}{CD} = \frac{AB}{CB} $。$\because AB = 2 \text{ m}$,$BC = 84 \text{ m}$,$AE = 1.5 \text{ m} $,$\therefore \frac{1.5}{CD} = \frac{2}{84} $,解得 $ CD = $
63
。答:二七纪念塔高度 $ CD $ 为63
m。
答案:
解:根据题意,得 $\angle EBA = \angle DBC $。$\because EA \perp AC$,$DC \perp AC $,$\therefore \angle EAB = \angle DCB = 90^\circ $。$\therefore \triangle ABE \backsim \triangle CBD $。$\therefore \frac{AE}{CD} = \frac{AB}{CB} $。$\because AB = 2 \text{ m}$,$BC = 84 \text{ m}$,$AE = 1.5 \text{ m} $,$\therefore \frac{1.5}{CD} = \frac{2}{84} $,解得 $ CD = 63 $。答:二七纪念塔高度 $ CD $ 为 63 m。
6. 为测量池塘边两点A,B之间的距离,小明设计了如下的方案:在地面取一点O,使AC,BD交于点O,且CD//AB. 若测得OB:OD= 3:2,CD= 40米,则A,B两点之间的距离为
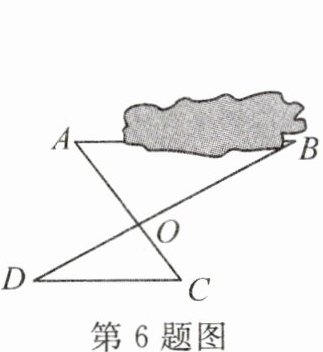
60
米.
答案:
60
7. 新考向 数学文化 四分仪是一种十分古老的测量仪器,其出现可追溯到数学家托勒密的《天文学大成》. 图1是古代测量员用四分仪测量一方井的深度,将四分仪置于方井上的边沿,通过窥衡杆测望井底点F,窥衡杆与四分仪的一边BC交于点H. 图2中,四分仪为正方形ABCD,方井为矩形BEFG. 若测量员从四分仪中读得AB为2,BH为1,实地测得BE为5,则井深BG为 (
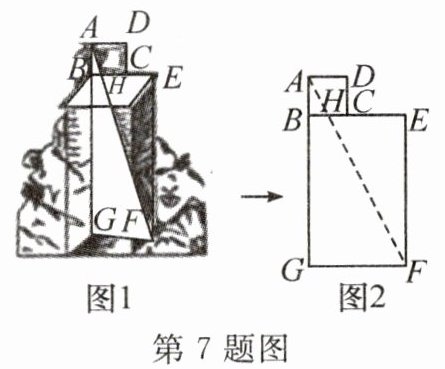
A. 7
B. 8
C. 9
D. 10
B
)
A. 7
B. 8
C. 9
D. 10
答案:
B
查看更多完整答案,请扫码查看


