第53页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
1. 有两个可以自由转动的转盘,每个转盘被等分成如图所示的几个扇形,游戏者同时转动两个转盘.如果一个转盘转出了红色,另一个转盘转出了蓝色,那么“配紫色”成功,游戏者获胜.则游戏者获胜的概率是
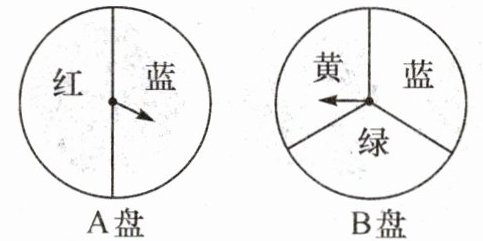
$\frac{1}{6}$
.
答案:
$\frac{1}{6}$
2. 如图,把一个转盘平均分成三份,依次标上数字1,2,3,自由转动转盘两次,把第一次转动停止后指针指向的数字记作x,把第二次转动停止后指针指向的数字记作y,则x与y的和为偶数的概率为
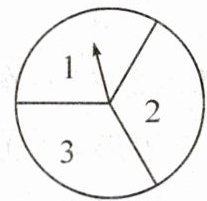
$\frac{5}{9}$
.
答案:
$\frac{5}{9}$
3. 用图中两个可以自由转动的转盘做“配紫色”游戏,分别转动两个转盘,若其中一个转出红色,另一个转出蓝色即可配成紫色,则配成紫色的概率是
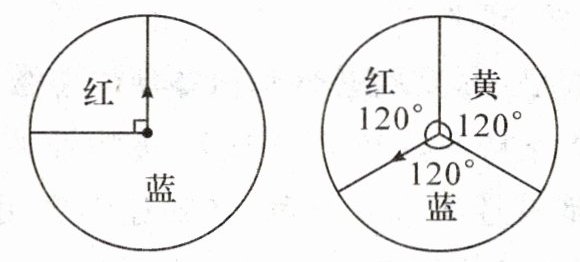
$\frac{1}{3}$
.
答案:
$\frac{1}{3}$
4. 用如图所示的两个可以自由转动的转盘做“配紫色游戏”,分别旋转两个转盘,若其中一个转出红色,另一个转出蓝色即可配成紫色.
(1)单独转动转盘A,指针指向红色区域的概率是
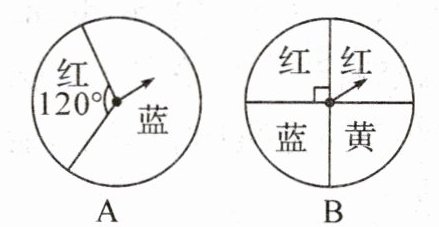
(2)同时转动两个转盘,求可配成紫色概率.
(1)单独转动转盘A,指针指向红色区域的概率是
$\frac{1}{3}$
.
(2)同时转动两个转盘,求可配成紫色概率.
列表略. 由表可知,共有12种等可能的结果,其中可配成紫色的结果有5种,∴可配成紫色的概率是$\frac{5}{12}$.
答案:
(1) $\frac{1}{3}$
(2) 列表略. 由表可知,共有12种等可能的结果,其中可配成紫色的结果有5种,
∴可配成紫色的概率是$\frac{5}{12}$.
(1) $\frac{1}{3}$
(2) 列表略. 由表可知,共有12种等可能的结果,其中可配成紫色的结果有5种,
∴可配成紫色的概率是$\frac{5}{12}$.
5. 宜昌景色宜人,其中三峡大坝、清江画廊、三峡人家景点的景色更是美不胜收.某民营单位为兼顾生产和业余生活,决定在下设的A,B,C三个部门利用转盘游戏确定参观的景点.两转盘各部分圆心角大小以及选派部门、旅游景点等信息如图.
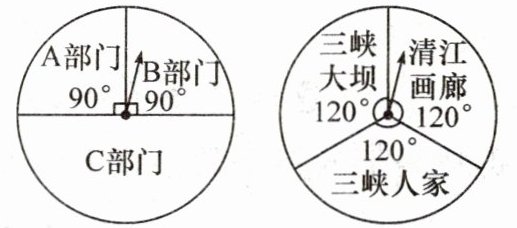
(1)若规定老同志相对偏多的部门选中的可能性大,试判断这个部门是哪个部门,请说明理由.
这个部门是
(2)设选中C部门游三峡大坝的概率为$P_1,$选中B部门游清江画廊或者三峡人家的概率为$P_2,$请判断$P_1,P_2$的大小关系,并说明理由.
$P_1$与$P_2$的大小关系是

(1)若规定老同志相对偏多的部门选中的可能性大,试判断这个部门是哪个部门,请说明理由.
这个部门是
C部门
. 理由:∵$P_{A}=\frac{90}{360}=\frac{1}{4}$,$P_{B}=\frac{90}{360}=\frac{1}{4}$,$P_{C}=\frac{180}{360}=\frac{1}{2}$,∴选中C部门的可能性最大. 故这个部门是C部门.(2)设选中C部门游三峡大坝的概率为$P_1,$选中B部门游清江画廊或者三峡人家的概率为$P_2,$请判断$P_1,P_2$的大小关系,并说明理由.
$P_1$与$P_2$的大小关系是
$P_{1}=P_{2}$
. 理由:将C部门等分成$C_{1}$,$C_{2}$两部分,列表略. 由表可知,共有12种等可能的结果,其中“C部门游三峡大坝”的结果有2种,“B部门游清江画廊或三峡人家”的结果也有2种,∴$P_{1}=\frac{2}{12}=\frac{1}{6}$,$P_{2}=\frac{2}{12}=\frac{1}{6}$. ∴$P_{1}=P_{2}$.
答案:
(1)C部门. 理由:
∵$P_{A}=\frac{90}{360}=\frac{1}{4}$,$P_{B}=\frac{90}{360}=\frac{1}{4}$,$P_{C}=\frac{180}{360}=\frac{1}{2}$,
∴选中C部门的可能性最大. 故这个部门是C部门.
(2)$P_{1}=P_{2}$. 理由:将C部门等分成$C_{1}$,$C_{2}$两部分,列表略. 由表可知,共有12种等可能的结果,其中“C部门游三峡大坝”的结果有2种,“B部门游清江画廊或三峡人家”的结果也有2种,
∴$P_{1}=\frac{2}{12}=\frac{1}{6}$,$P_{2}=\frac{2}{12}=\frac{1}{6}$.
∴$P_{1}=P_{2}$.
(1)C部门. 理由:
∵$P_{A}=\frac{90}{360}=\frac{1}{4}$,$P_{B}=\frac{90}{360}=\frac{1}{4}$,$P_{C}=\frac{180}{360}=\frac{1}{2}$,
∴选中C部门的可能性最大. 故这个部门是C部门.
(2)$P_{1}=P_{2}$. 理由:将C部门等分成$C_{1}$,$C_{2}$两部分,列表略. 由表可知,共有12种等可能的结果,其中“C部门游三峡大坝”的结果有2种,“B部门游清江画廊或三峡人家”的结果也有2种,
∴$P_{1}=\frac{2}{12}=\frac{1}{6}$,$P_{2}=\frac{2}{12}=\frac{1}{6}$.
∴$P_{1}=P_{2}$.
查看更多完整答案,请扫码查看


