第3页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
11. (2024·临夏州)如图,$O$是坐标原点,菱形$ABOC的顶点B在x$轴的负半轴上,顶点$C的坐标为(3,4)$,则顶点$A$的坐标为(
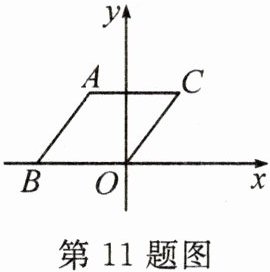
A. $(-4,2)$
B. $(-\sqrt{3},4)$
C. $(-2,4)$
D. $(-4,\sqrt{3})$
C
)
A. $(-4,2)$
B. $(-\sqrt{3},4)$
C. $(-2,4)$
D. $(-4,\sqrt{3})$
答案:
C
12. (2024·海南)如图,菱形$ABCD的边长为2$,$\angle ABC = 120^{\circ}$,边$AB$在数轴上,将$AC绕点A$顺时针旋转,点$C落在数轴上的点E$处. 若点$E表示的数是3$,则点$A$表示的数是

$3-2\sqrt {3}$
.
答案:
$3-2\sqrt {3}$
13. 如图,在菱形ABCD中,对角线AC,BD相交于点O,过点D作对角线BD的垂线交BA的延长线于点E.(1)求证:四边形ACDE是平行四边形.(2)若AC = 8,BD = 6,求$\triangle ADE$的周长. (1)证明:∵ 四边形 ABCD 是菱形,$\therefore AB// CD,AC⊥BD.\therefore AE// CD,∠AOB=90^{\circ }. $∵ DE⊥BD,即$∠EDB=90^{\circ },\therefore ∠AOB=∠EDB.\therefore DE// AC. $∴ 四边形 ACDE 是平行四边形. (2)∵ 四边形 ABCD 是菱形,$AC=8,BD=6,\therefore AO=4,DO=3.\therefore AD=CD=\sqrt {AO^{2}+DO^{2}}=5. $∵ 四边形 ACDE 是平行四边形,$\therefore AE=CD=5,DE=AC=8.\therefore \triangle ADE$的周长为 AD+AE+DE=5+5+8=
(1)证明:∵ 四边形 ABCD 是菱形,$\therefore AB// CD,AC⊥BD.\therefore AE// CD,∠AOB=90^{\circ }. $∵ DE⊥BD,即$∠EDB=90^{\circ },\therefore ∠AOB=∠EDB.\therefore DE// AC. $∴ 四边形 ACDE 是平行四边形. (2)∵ 四边形 ABCD 是菱形,$AC=8,BD=6,\therefore AO=4,DO=3.\therefore AD=CD=\sqrt {AO^{2}+DO^{2}}=5. $∵ 四边形 ACDE 是平行四边形,$\therefore AE=CD=5,DE=AC=8.\therefore \triangle ADE$的周长为 AD+AE+DE=5+5+8=
 (1)证明:∵ 四边形 ABCD 是菱形,$\therefore AB// CD,AC⊥BD.\therefore AE// CD,∠AOB=90^{\circ }. $∵ DE⊥BD,即$∠EDB=90^{\circ },\therefore ∠AOB=∠EDB.\therefore DE// AC. $∴ 四边形 ACDE 是平行四边形. (2)∵ 四边形 ABCD 是菱形,$AC=8,BD=6,\therefore AO=4,DO=3.\therefore AD=CD=\sqrt {AO^{2}+DO^{2}}=5. $∵ 四边形 ACDE 是平行四边形,$\therefore AE=CD=5,DE=AC=8.\therefore \triangle ADE$的周长为 AD+AE+DE=5+5+8=
(1)证明:∵ 四边形 ABCD 是菱形,$\therefore AB// CD,AC⊥BD.\therefore AE// CD,∠AOB=90^{\circ }. $∵ DE⊥BD,即$∠EDB=90^{\circ },\therefore ∠AOB=∠EDB.\therefore DE// AC. $∴ 四边形 ACDE 是平行四边形. (2)∵ 四边形 ABCD 是菱形,$AC=8,BD=6,\therefore AO=4,DO=3.\therefore AD=CD=\sqrt {AO^{2}+DO^{2}}=5. $∵ 四边形 ACDE 是平行四边形,$\therefore AE=CD=5,DE=AC=8.\therefore \triangle ADE$的周长为 AD+AE+DE=5+5+8=18
.
答案:
解:
(1)证明:
∵ 四边形 ABCD 是菱形,$\therefore AB// CD,AC⊥BD.$$\therefore AE// CD,∠AOB=90^{\circ }$.
∵ DE$⊥BD$,即$∠EDB=90^{\circ },\therefore $$∠AOB=∠EDB.\therefore DE// AC$.
∴ 四边形 ACDE 是平行四边形.
(2)
∵ 四边形 ABCD 是菱形,$AC=8,BD=6,\therefore AO=4,DO$$=3.\therefore AD=CD=\sqrt {AO^{2}+DO^{2}}=5$.
∵ 四边形 ACDE 是平行四边形,$\therefore AE=CD=5,DE=AC=8.\therefore \triangle ADE$的周长为 AD$+AE+DE=5+5+8=18.$
(1)证明:
∵ 四边形 ABCD 是菱形,$\therefore AB// CD,AC⊥BD.$$\therefore AE// CD,∠AOB=90^{\circ }$.
∵ DE$⊥BD$,即$∠EDB=90^{\circ },\therefore $$∠AOB=∠EDB.\therefore DE// AC$.
∴ 四边形 ACDE 是平行四边形.
(2)
∵ 四边形 ABCD 是菱形,$AC=8,BD=6,\therefore AO=4,DO$$=3.\therefore AD=CD=\sqrt {AO^{2}+DO^{2}}=5$.
∵ 四边形 ACDE 是平行四边形,$\therefore AE=CD=5,DE=AC=8.\therefore \triangle ADE$的周长为 AD$+AE+DE=5+5+8=18.$
14. 如图,在边长为$4的菱形ABCD$中,$\angle BAD = 120^{\circ}$,$E$,$F分别是边BC$,$CD$上的两个动点,$\angle EAF = 60^{\circ}$.
(1)试判断$\triangle AEF$的形状,并说明理由.
(2)求四边形$AECF$的面积.

【拓展设问】在点$E$,$F$运动的过程中,$\triangle CEF$的面积存在最大值吗?若存在,则最大值为______.
【拓展设问】
(1)试判断$\triangle AEF$的形状,并说明理由.
(2)求四边形$AECF$的面积.

【拓展设问】在点$E$,$F$运动的过程中,$\triangle CEF$的面积存在最大值吗?若存在,则最大值为______.
(1)$\triangle AEF$是等边三角形. 理由如下:连接 AC. ∵ 四边形ABCD 是菱形,$\therefore AD=CD,AB// DC,AD// BC.\therefore ∠ACE=∠CAD.\because ∠BAD=120^{\circ },\therefore ∠D=180^{\circ }-∠BAD=60^{\circ }.\therefore \triangle ADC$是等边三角形.$\therefore AC=AD,∠CAD=∠D=60^{\circ }.\therefore ∠ACE=∠D.\because ∠EAF=60^{\circ },\therefore ∠EAF-∠CAF=∠CAD-∠CAF$,即$∠CAE=∠DAF$. 在$\triangle CAE$和$\triangle DAF$中,$\left\{\begin{array}{l} ∠CAE=∠DAF,\\ CA=DA,\\ ∠ACE=∠ADF,\end{array}\right. $$\therefore \triangle CAE\cong \triangle DAF(ASA).\therefore AE=AF$. 又$\because ∠EAF=60^{\circ },\therefore \triangle AEF$为等边三角形. (2)过点 A 作$AM⊥CD$于点 M. ∵ 四边形 ABCD 是菱形,$\therefore AD=CD=4.\because \triangle ADC$是等边三角形,$AM⊥CD,\therefore DM=\frac {1}{2}CD=2.\therefore AM=\sqrt {AD^{2}-DM^{2}}=\sqrt {4^{2}-2^{2}}=2\sqrt {3}$. 由(1)可知,$\triangle CAE\cong \triangle DAF,\therefore S_{\triangle CAE}=S_{\triangle DAF},\therefore S_{四边形AECF}=S_{\triangle ADC}=\frac {1}{2}CD\cdot AM=\frac {1}{2}×4×2\sqrt {3}=4\sqrt {3}$.
【拓展设问】
$\sqrt {3}$
答案:
解:
(1)$\triangle AEF$是等边三角形. 理由如下:连接 AC.
∵ 四边形ABCD 是菱形,$\therefore AD=CD,AB// DC,AD// BC.\therefore ∠ACE=$$∠CAD.\because ∠BAD=120^{\circ },\therefore ∠D=180^{\circ }-∠BAD=60^{\circ }.\therefore $$\triangle ADC$是等边三角形.$\therefore AC=AD,∠CAD=∠D=60^{\circ }.\therefore $$∠ACE=∠D.\because ∠EAF=60^{\circ },\therefore ∠EAF-∠CAF=∠CAD-$$∠CAF$,即$∠CAE=∠DAF$. 在$\triangle CAE$和$\triangle DAF$中,$\left\{\begin{array}{l} ∠CAE=∠DAF,\\ CA=DA,\\ ∠ACE=∠ADF,\end{array}\right. $$\therefore \triangle CAE\cong \triangle DAF(ASA).\therefore AE=AF$. 又$\because ∠EAF=60^{\circ },\therefore \triangle AEF$为等边三角形.
(2)过点 A 作$AM⊥$CD 于点 M.
∵ 四边形 ABCD 是菱形,$\therefore AD=CD=4.\because $$\triangle ADC$是等边三角形,$AM⊥CD,\therefore DM=\frac {1}{2}CD=2.\therefore AM=$$\sqrt {AD^{2}-DM^{2}}=\sqrt {4^{2}-2^{2}}=2\sqrt {3}$. 由
(1)可知,$\triangle CAE\cong $$\triangle DAF,\therefore S_{\triangle CAE}=S_{\triangle DAF},\therefore S_{四边形AECF}=S_{\triangle ADC}=\frac {1}{2}CD\cdot AM=$$\frac {1}{2}×4×2\sqrt {3}=4\sqrt {3}$.【拓展设问】$\sqrt {3}$
(1)$\triangle AEF$是等边三角形. 理由如下:连接 AC.
∵ 四边形ABCD 是菱形,$\therefore AD=CD,AB// DC,AD// BC.\therefore ∠ACE=$$∠CAD.\because ∠BAD=120^{\circ },\therefore ∠D=180^{\circ }-∠BAD=60^{\circ }.\therefore $$\triangle ADC$是等边三角形.$\therefore AC=AD,∠CAD=∠D=60^{\circ }.\therefore $$∠ACE=∠D.\because ∠EAF=60^{\circ },\therefore ∠EAF-∠CAF=∠CAD-$$∠CAF$,即$∠CAE=∠DAF$. 在$\triangle CAE$和$\triangle DAF$中,$\left\{\begin{array}{l} ∠CAE=∠DAF,\\ CA=DA,\\ ∠ACE=∠ADF,\end{array}\right. $$\therefore \triangle CAE\cong \triangle DAF(ASA).\therefore AE=AF$. 又$\because ∠EAF=60^{\circ },\therefore \triangle AEF$为等边三角形.
(2)过点 A 作$AM⊥$CD 于点 M.
∵ 四边形 ABCD 是菱形,$\therefore AD=CD=4.\because $$\triangle ADC$是等边三角形,$AM⊥CD,\therefore DM=\frac {1}{2}CD=2.\therefore AM=$$\sqrt {AD^{2}-DM^{2}}=\sqrt {4^{2}-2^{2}}=2\sqrt {3}$. 由
(1)可知,$\triangle CAE\cong $$\triangle DAF,\therefore S_{\triangle CAE}=S_{\triangle DAF},\therefore S_{四边形AECF}=S_{\triangle ADC}=\frac {1}{2}CD\cdot AM=$$\frac {1}{2}×4×2\sqrt {3}=4\sqrt {3}$.【拓展设问】$\sqrt {3}$
查看更多完整答案,请扫码查看


