《2025年名校课堂九年级数学上册北师大版》

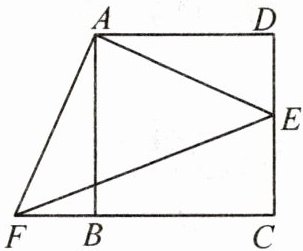
11. 如图,四边形ABCD是正方形,E,F分别是DC和CB的延长线上的点,且$DE= BF$,连接AE,AF,EF.若$BC= 8$,$DE= 3$,则EF的长为$\sqrt {146}$.

答案： $\sqrt {146}$

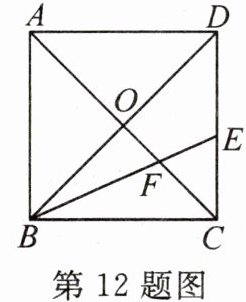
12. 如图,在正方形ABCD中,AC与BD交于点O,BE平分$∠CBD$,交CD于点E,交OC于点F.若$AB= 4$,则$CF= $$4\sqrt {2}-4$.

答案： $4\sqrt {2}-4$

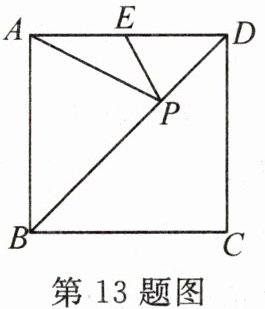
13. 如图,在一个边长为6的正方形ABCD中,E为AD的中点,P为对角线BD上的一个动点,则$AP+EP$的最小值是$3\sqrt {5}$.

答案： $3\sqrt {5}$

14. 如图,在正方形ABCD中,对角线AC,BD相交于点O,E,F是对角线AC上的两点,且$AE= CF$,连接DE,DF,BE,BF.
(1)求证:$△ADE≌△CBF$.
证明：$\because$四边形$ABCD$是正方形，$\therefore \angle DAE=\angle BCF = 45^{\circ}$，$AD = CB$．在$\triangle ADE$和$\triangle CBF$中，$\left\{\begin{array}{l} AD = CB,\\ \angle DAE = \angle BCF,\\ AE = CF,\end{array}\right.$$\therefore \triangle ADE≌\triangle CBF$(SAS)．
(2)若$AB= 4\sqrt{2}$,$AE= 2$,求四边形BEDF的周长.
解：$\because AB = AD = 4\sqrt {2}$，$\therefore BD =\sqrt {AB^{2}+AD^{2}}=\sqrt {(4\sqrt {2})^{2}+(4\sqrt {2})^{2}} = 8$．$\because$四边形$ABCD$是正方形，$\therefore AC = BD = 8$，$BD\perp EF$．$\therefore DO = BO = OA = OC = 4$．又$\because AE = CF = 2$，$\therefore OE = OA - AE = 4 - 2 = 2$，$OF = OC - CF$，即$OE = OF = 4 - 2 = 2$．$\therefore$四边形$BEDF$为菱形．$\because DE=\sqrt {DO^{2}+EO^{2}}=\sqrt {4^{2}+2^{2}} = 2\sqrt {5}$，$\therefore$四边形$BEDF$的周长为$8\sqrt{5}$．

答案： 解：
(1)证明：$\because$四边形$ABCD$是正方形，$\therefore \angle DAE=\angle BCF = 45^{\circ}$，$AD = CB$．在$\triangle ADE$和$\triangle CBF$中，$\left\{\begin{array}{l} AD = CB,\\ \angle DAE = \angle BCF,\\ AE = CF,\end{array}\right.$$\therefore \triangle ADE\cong \triangle CBF(SAS)$．
(2)$\because AB = AD = 4\sqrt {2}$，$\therefore BD =\sqrt {AB^{2}+AD^{2}}=\sqrt {(4\sqrt {2})^{2}+(4\sqrt {2})^{2}} = 8$．$\because$四边形$ABCD$是正方形，$\therefore AC = BD = 8$，$BD\perp EF$．$\therefore DO = BO = OA = OC = 4$．又$\because AE = CF = 2$，$\therefore OE = OA - AE = 4 - 2 = 2$，$OF = OC - CF$，即$OE = OF = 4 - 2 = 2$．$\therefore$四边形$BEDF$为菱形．$\because DE=\sqrt {DO^{2}+EO^{2}}=\sqrt {4^{2}+2^{2}} = 2\sqrt {5}$，$\therefore$四边形$BEDF$的周长为$4DE = 8\sqrt {5}$．

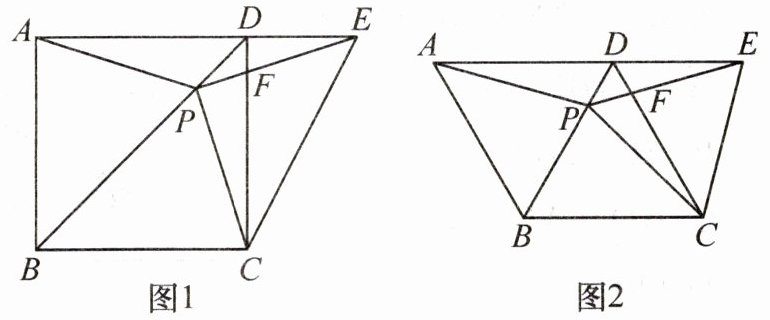
15. 如图1,在正方形ABCD中,P为对角线BD上的一点,点E在AD的延长线上,且$PA= PE$,$PE$交CD于点F,连接CE.
(1)求证:$△PCE$是等腰直角三角形.
(2)如图2,把正方形ABCD改为菱形ABCD,其他条件不变,当$∠ABC= 120^{\circ}$时,判断$△PCE$的形状,并说明理由.

(1)证明：$\because$四边形$ABCD$是正方形，$\therefore DA = DC$，$\angle ADP=\angle CDP = 45^{\circ}$，$\angle ADC = 90^{\circ}$．在$\triangle PDA$和$\triangle PDC$中，$\left\{\begin{array}{l} PD = PD,\\ \angle ADP = \angle CDP,\\ DA = DC,\end{array}\right.$$\therefore \triangle PDA\cong \triangle PDC(SAS)$．$\therefore PA = PC$，$\angle PAD = \angle PCD$．$\because PA = PE$，$\therefore PE = PC$，$\angle PEA = \angle PAD$．$\therefore \angle PCD = \angle PEA$．$\because \angle EDF = 90^{\circ}$，$\angle DFE = \angle PFC$，$\therefore \angle FPC = \angle EDF = 90^{\circ}$．$\therefore \triangle PCE$是等腰直角三角形．
(2)$\triangle PCE$是等边三角形．理由：$\because$四边形$ABCD$是菱形，$\therefore DA = DC$，$\angle ADP = \angle CDP$，$\angle ADC = \angle ABC = 120^{\circ}$．在$\triangle PDA$和$\triangle PDC$中，$\left\{\begin{array}{l} PD = PD,\\ \angle ADP = \angle CDP,\\ DA = DC,\end{array}\right.$$\therefore \triangle PDA\cong \triangle PDC(SAS)$．$\therefore PA = PC$，$\angle PAD = \angle PCD$．$\because PA = PE$，$\therefore \angle PEA = \angle PAD$，$PE = PC$．$\therefore \angle PCD = \angle PEA$．$\because \angle DFE = \angle PFC$，$\therefore \angle EPC = \angle EDC$．$\because \angle ADC = 120^{\circ}$，$\therefore \angle EDC = 60^{\circ}$．$\therefore \angle EPC = 60^{\circ}$．$\therefore \triangle PCE$是等边三角形．

答案： 解：
(1)证明：$\because$四边形$ABCD$是正方形，$\therefore DA = DC$，$\angle ADP=\angle CDP = 45^{\circ}$，$\angle ADC = 90^{\circ}$．在$\triangle PDA$和$\triangle PDC$中，$\left\{\begin{array}{l} PD = PD,\\ \angle ADP = \angle CDP,\\ DA = DC,\end{array}\right.$$\therefore \triangle PDA\cong \triangle PDC(SAS)$．$\therefore PA = PC$，$\angle PAD = \angle PCD$．$\because PA = PE$，$\therefore PE = PC$，$\angle PEA = \angle PAD$．$\therefore \angle PCD = \angle PEA$．$\because \angle EDF = 90^{\circ}$，$\angle DFE = \angle PFC$，$\therefore \angle FPC = \angle EDF = 90^{\circ}$．$\therefore \triangle PCE$是等腰直角三角形．
(2)$\triangle PCE$是等边三角形．理由：$\because$四边形$ABCD$是菱形，$\therefore DA = DC$，$\angle ADP = \angle CDP$，$\angle ADC = \angle ABC = 120^{\circ}$．在$\triangle PDA$和$\triangle PDC$中，$\left\{\begin{array}{l} PD = PD,\\ \angle ADP = \angle CDP,\\ DA = DC,\end{array}\right.$$\therefore \triangle PDA\cong \triangle PDC(SAS)$．$\therefore PA = PC$，$\angle PAD = \angle PCD$．$\because PA = PE$，$\therefore \angle PEA = \angle PAD$，$PE = PC$．$\therefore \angle PCD = \angle PEA$．$\because \angle DFE = \angle PFC$，$\therefore \angle EPC = \angle EDC$．$\because \angle ADC = 120^{\circ}$，$\therefore \angle EDC = 60^{\circ}$．$\therefore \angle EPC = 60^{\circ}$．$\therefore \triangle PCE$是等边三角形．