《2025年名校课堂九年级数学上册北师大版》

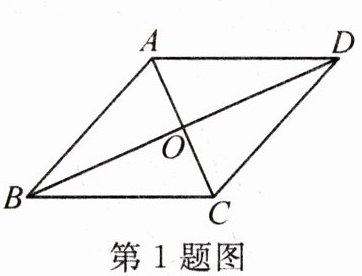
1. 如图,四边形ABCD是菱形,对角线AC,BD相交于点O.若AC= 6cm,BD= 8cm,则菱形的面积为(C)
$A. 12cm^2 B. 6cm^2 C. 24cm^2 D. 48cm^2$

答案： C

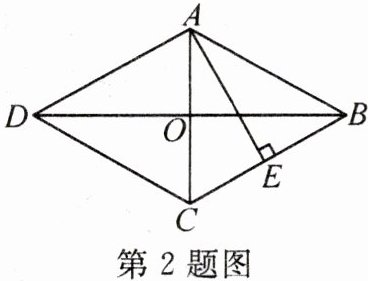
2. (2024·绥化改编)如图,四边形ABCD是菱形,BC= 5,BD= 8,则菱形ABCD的面积为24.
【拓展提问】若AE⊥BC于点E,则AE的长是$\frac{24}{5}$.

答案： 24 【拓展提问】$\frac{24}{5}$

3. 如图,菱形花坛ABCD的一边长AB为20m,∠ABC= 60°,沿着该菱形的对角线修建两条小路AC和BD.
(1)求AC和BD的长.AC的长为20m，BD的长为20√3m.
(2)求菱形花坛ABCD的面积.菱形花坛ABCD的面积为200√3m².

答案： 解：
(1)
∵四边形$ABCD$是菱形，$∠ABC = 60^{\circ}$，
∴$AC⊥BD$，$AO = CO$，$BO = DO$，$∠ABD=\frac{1}{2}∠ABC = 30^{\circ}$．
∴$AO=\frac{1}{2}AB = 10m$．
∴$AC = 2AO = 20m$，$BO=\sqrt{AB^{2}-AO^{2}}=\sqrt{20^{2}-10^{2}} = 10\sqrt{3}(m)$．
∴$BD = 2BO = 20\sqrt{3}m$．
(2)$S_{菱形花坛ABCD}=S_{\triangle ABD}+S_{\triangle BCD}=\frac{1}{2}BD\cdot AO+\frac{1}{2}BD\cdot OC=\frac{1}{2}BD\cdot(AO + OC)=\frac{1}{2}BD\cdot AC=\frac{1}{2}\times20\times20\sqrt{3}=200\sqrt{3}(m^{2})$．

4. 下列说法中,不正确的是(C)
A. 四边相等的四边形是菱形
B. 对角线垂直的平行四边形是菱形
C. 菱形的对角线互相垂直且相等
D. 菱形的邻边相等

答案： C

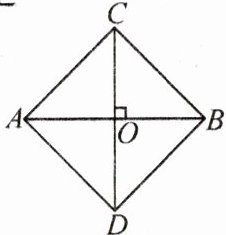
5. 如图,O既是AB的中点,又是CD的中点,且AB⊥CD,连接AC,BC,AD,BD.若AC= 3,则四边形ACBD的周长是(B)

A. 6
B. 12
C. 18
D. 不能确定

答案： B

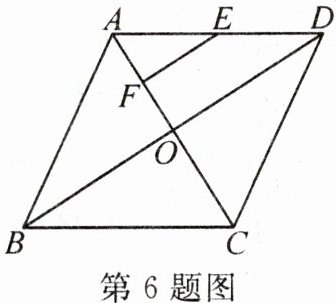
6. 如图,在平行四边形ABCD中,对角线AC,BD相交于点O,AB= AD,E,F分别为AD,AO的中点,连接EF.若EF= 3,AO= 4,则AD的长为(A)

A. 2√{13}
B. 10
C. 5
D. √{13}

答案： A

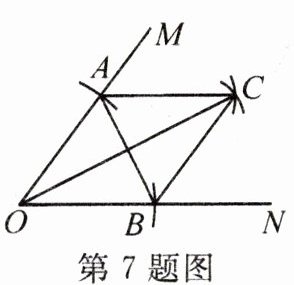
7. 如图,在∠MON的两边上分别截取OA,OB,使OA= OB,分别以点A,B为圆心,OA的长为半径作弧,两弧交于点C,连接AC,BC,AB,OC.若AB= 2cm,四边形OACB的面积为$4cm^2,$则OC的长为4cm.

答案： 4

8. 新考向 真实情境 小颖买了一盏简单而精致的吊灯(图1),其侧面的示意图如图2所示,四边形ABCD是一个菱形外框架,对角线AC,BD相交于点O,四边形AECF是其内部框架,且点E,F在BD上,BE= DF. 求证：四边形内部框架AECF为菱形.
证明：∵四边形$ABCD$是菱形，∴$OB = OD$，$OA = OC$．∵$BE = DF$，∴$OB - BE = OD - DF$，即$OE = OF$．∴四边形$AECF$是平行四边形．∵四边形$ABCD$是菱形，∴$AC⊥BD$．∴平行四边形$AECF$是菱形．

答案： 证明：
∵四边形$ABCD$是菱形，
∴$OB = OD$，$OA = OC$．
∵$BE = DF$，
∴$OB - BE = OD - DF$，即$OE = OF$．
∴四边形$AECF$是平行四边形．
∵四边形$ABCD$是菱形，
∴$AC⊥BD$．
∴平行四边形$AECF$是菱形．