第9页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
10. 如图,在矩形ABCD中,E是边AD上一点,F,G分别是BE,CE的中点,连接AF,DG,FG. 若$AF= 3,DG= 4,FG= 5$,则矩形ABCD的面积为
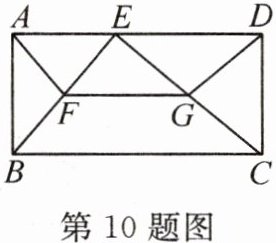
48
.
答案:
48
11. 如图,在矩形ABCD中,以点A为圆心,AB的长为半径画弧交AD于点E,交AC于点F,连接EF,以点F为圆心,EF的长为半径画弧,与弧BE交于点G,射线AG交BC于点H. 若$AD= 8,BH= 3$,则AB的长为

4
.
答案:
4
12. (2023·哈尔滨)矩形ABCD的对角线AC,BD相交于点O,点F在矩形ABCD的边上,连接OF. 若$\angle ADB= 38^{\circ},\angle BOF= 30^{\circ}$,则$\angle AOF= $
46°或106°
.
答案:
46°或106°
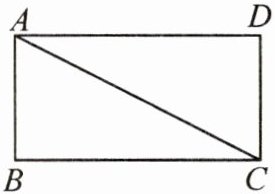
13. 如图,在矩形ABCD中,AC是对角线.
(1)实践与操作:作线段AC的垂直平分线,垂足为O,交边AD于点E,交边BC于点F(要求:尺规作图,保留作图痕迹,不写作法,标明字母).
(2)猜想与证明:试猜想线段AE与CF的数量关系,并加以证明.
(3)连接AF,若$AB= 6,BC= 8$,则BF的长
为
(1)实践与操作:作线段AC的垂直平分线,垂足为O,交边AD于点E,交边BC于点F(要求:尺规作图,保留作图痕迹,不写作法,标明字母).
(2)猜想与证明:试猜想线段AE与CF的数量关系,并加以证明.
(3)连接AF,若$AB= 6,BC= 8$,则BF的长

为
$\frac{7}{4}$
.
答案:
1. (1)尺规作图步骤:
以$A$为圆心,大于$\frac{1}{2}AC$的长为半径画弧;
以$C$为圆心,同样长为半径画弧,两弧分别相交于两点;
过这两点作直线,与$AC$交于$O$,与$AD$交于$E$,与$BC$交于$F$。(作图痕迹略)
2. (2)
猜想:$AE = CF$。
证明:
因为四边形$ABCD$是矩形,所以$AD// BC$,则$\angle EAO=\angle FCO$。
因为$EF$是$AC$的垂直平分线,所以$AO = CO$,$\angle AOE=\angle COF = 90^{\circ}$。
在$\triangle AOE$和$\triangle COF$中,$\left\{\begin{array}{l}\angle EAO=\angle FCO\\AO = CO\\\angle AOE=\angle COF\end{array}\right.$。
根据$ASA$(角 - 边 - 角)定理,可得$\triangle AOE\cong\triangle COF$。
所以$AE = CF$。
3. (3)
设$BF=x$,则$CF = 8 - x$,因为$AE = CF$,所以$AE = 8 - x$,$DE=AD - AE=8-(8 - x)=x$。
在$Rt\triangle ABF$中,$AF^{2}=AB^{2}+BF^{2}=6^{2}+x^{2}$;在$Rt\triangle CDE$中,$CE^{2}=CD^{2}+DE^{2}=6^{2}+x^{2}$(因为$AB = CD = 6$),又因为$EF$垂直平分$AC$,所以$AF = CF$。
则$CF^{2}=AB^{2}+BF^{2}$,即$(8 - x)^{2}=6^{2}+x^{2}$。
展开得$64-16x+x^{2}=36 + x^{2}$。
移项得$64-36=16x$。
即$16x = 28$,解得$x=\frac{7}{4}$。
故$BF$的长为$\frac{7}{4}$。
以$A$为圆心,大于$\frac{1}{2}AC$的长为半径画弧;
以$C$为圆心,同样长为半径画弧,两弧分别相交于两点;
过这两点作直线,与$AC$交于$O$,与$AD$交于$E$,与$BC$交于$F$。(作图痕迹略)
2. (2)
猜想:$AE = CF$。
证明:
因为四边形$ABCD$是矩形,所以$AD// BC$,则$\angle EAO=\angle FCO$。
因为$EF$是$AC$的垂直平分线,所以$AO = CO$,$\angle AOE=\angle COF = 90^{\circ}$。
在$\triangle AOE$和$\triangle COF$中,$\left\{\begin{array}{l}\angle EAO=\angle FCO\\AO = CO\\\angle AOE=\angle COF\end{array}\right.$。
根据$ASA$(角 - 边 - 角)定理,可得$\triangle AOE\cong\triangle COF$。
所以$AE = CF$。
3. (3)
设$BF=x$,则$CF = 8 - x$,因为$AE = CF$,所以$AE = 8 - x$,$DE=AD - AE=8-(8 - x)=x$。
在$Rt\triangle ABF$中,$AF^{2}=AB^{2}+BF^{2}=6^{2}+x^{2}$;在$Rt\triangle CDE$中,$CE^{2}=CD^{2}+DE^{2}=6^{2}+x^{2}$(因为$AB = CD = 6$),又因为$EF$垂直平分$AC$,所以$AF = CF$。
则$CF^{2}=AB^{2}+BF^{2}$,即$(8 - x)^{2}=6^{2}+x^{2}$。
展开得$64-16x+x^{2}=36 + x^{2}$。
移项得$64-36=16x$。
即$16x = 28$,解得$x=\frac{7}{4}$。
故$BF$的长为$\frac{7}{4}$。
14. 新考向 阅读理解 请阅读下列材料,并完成相应的任务.
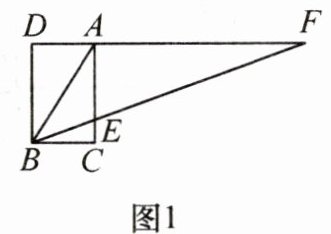
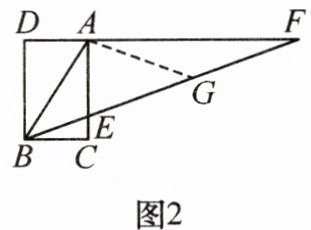
三等分角是古希腊三大几何问题之一. 如图1,任意锐角$\angle ABC$可看作矩形BCAD的对角线BA和边BC的夹角,以B为端点的射线BF交CA于点E,交DA的延长线于点F. 若$EF= 2AB$,则射线BF是$\angle ABC$的一条三等分线.
证明:如图2,取EF的中点G,连接AG……
任务:
(1)完成材料中的证明过程.
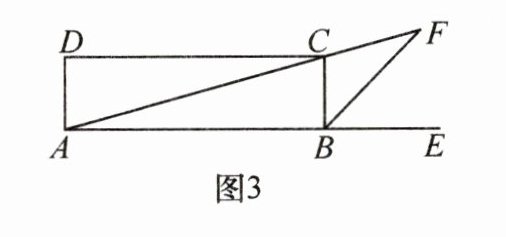
(2)如图3,在矩形ABCD中,对角线AC的延长线与外角$\angle CBE$的平分线相交于点F. 若$BF= \frac{1}{2}AC$,则$\angle F$的度数为____.
三等分角是古希腊三大几何问题之一. 如图1,任意锐角$\angle ABC$可看作矩形BCAD的对角线BA和边BC的夹角,以B为端点的射线BF交CA于点E,交DA的延长线于点F. 若$EF= 2AB$,则射线BF是$\angle ABC$的一条三等分线.
证明:如图2,取EF的中点G,连接AG……
任务:
(1)完成材料中的证明过程.
(2)如图3,在矩形ABCD中,对角线AC的延长线与外角$\angle CBE$的平分线相交于点F. 若$BF= \frac{1}{2}AC$,则$\angle F$的度数为____.



(1)证明:∵四边形BCAD是矩形,∴AD//BC,∠DAC=90°。∴∠F=∠CBF,∠EAF=90°。∵G是EF的中点,∴AG=$\frac{1}{2}$EF=FG。∴∠F=∠GAF。∵EF=2AB,∴AG=AB。∴∠ABG=∠AGB=∠F+∠GAF=2∠F=2∠CBF。∴∠ABC=3∠CBF。∴射线BF是∠ABC的一条三等分线。
30°
答案:
解:
(1)证明:
∵四边形BCAD是矩形,
∴AD//BC,∠DAC=90°。
∴∠F=∠CBF,∠EAF=90°。
∵G是EF的中点,
∴AG=$\frac{1}{2}$EF=FG。
∴∠F=∠GAF。
∵EF=2AB,
∴AG=AB。
∴∠ABG=∠AGB=∠F+∠GAF=2∠F=2∠CBF。
∴∠ABC=3∠CBF。
∴射线BF是∠ABC的一条三等分线。
(2)30°
(1)证明:
∵四边形BCAD是矩形,
∴AD//BC,∠DAC=90°。
∴∠F=∠CBF,∠EAF=90°。
∵G是EF的中点,
∴AG=$\frac{1}{2}$EF=FG。
∴∠F=∠GAF。
∵EF=2AB,
∴AG=AB。
∴∠ABG=∠AGB=∠F+∠GAF=2∠F=2∠CBF。
∴∠ABC=3∠CBF。
∴射线BF是∠ABC的一条三等分线。
(2)30°
查看更多完整答案,请扫码查看


