第12页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
1. 已知在四边形 $ABCD$ 中,$\angle A= \angle B= \angle C = 90^{\circ}$,对角线 $AC$,$BD$ 相交于点 $O$。下列结论一定成立的是(
A. $AC\perp BD$
B. $AC = BD$
C. $AB = BC$
D. $AB = AC$
B
)A. $AC\perp BD$
B. $AC = BD$
C. $AB = BC$
D. $AB = AC$
答案:
B
2. 如图,在矩形 $ABCD$ 中,$AC$,$BD$ 相交于点 $O$。若 $\triangle AOB$ 的面积是 $3$,则矩形 $ABCD$ 的面积是(
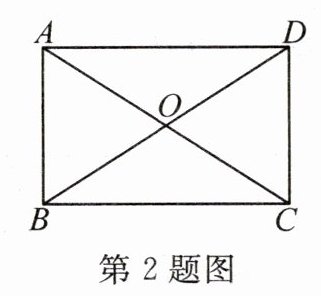
A. $6$
B. $9$
C. $12$
D. $15$
C
)
A. $6$
B. $9$
C. $12$
D. $15$
答案:
C
3. 如图,用一根绳子检查一个平行四边形书架的侧边是否和上、下底都垂直,只需要用绳子分别测量比较书架的两条对角线 $AC$,$BD$ 就可以判断,其推理依据是(
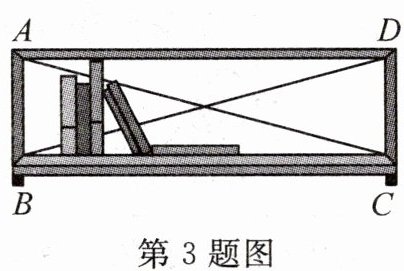
A. 矩形的对角线相等
B. 矩形的四个角是直角
C. 对角线相等的四边形是矩形
D. 对角线相等的平行四边形是矩形
D
)
A. 矩形的对角线相等
B. 矩形的四个角是直角
C. 对角线相等的四边形是矩形
D. 对角线相等的平行四边形是矩形
答案:
D
4. 新考向 真实情境 图1是某种型号拉杆箱的实物图,图2是它的几何示意图,行李箱的侧面可看成一个矩形,点 $F$,$C$,$D$ 在同一直线上,$\angle D = 35^{\circ}$,为了拉箱时的舒适度,现将 $\angle ABD$ 调整为 $75^{\circ}$,$\angle D$ 保持不变,则图中 $\angle ECF$ 应为
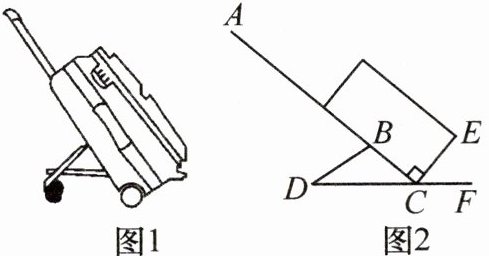
$50^{\circ}$
。
答案:
$50^{\circ}$
5. 如图,在矩形 $ABCD$ 中,$AC$ 和 $BD$ 相交于点 $O$,$AC = 2AB$,则 $\angle AOD$ 的度数等于
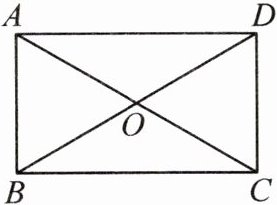
$120^{\circ}$
。
答案:
$120^{\circ}$
6. 如图,在 $□ ABCD$ 中,$\angle ACB= \angle DBC$。
(1)求证:平行四边形 $ABCD$ 是矩形。
(2)若 $AB = 2$,$\angle ACB = 30^{\circ}$,求 $BC$ 的长。
(1)证明: $\because \angle ACB=\angle DBC,\therefore BO=CO$. $\because$ 四边形 $ABCD$ 是平行四边形, $\therefore AC=2OC,BD=2OB$. $\therefore AC=BD$. $\therefore$ 平行四边形 $ABCD$ 是矩形.
(2) $\because$ 在矩形 $ABCD$ 中, $\angle ABC=90^{\circ},\therefore \triangle ABC$ 是直角三角形. $\because \angle ACB=30^{\circ},\therefore AC=2AB=2× 2=4$. $\therefore BC=\sqrt{AC^{2}-AB^{2}}=\sqrt{4^{2}-2^{2}}=$
(1)求证:平行四边形 $ABCD$ 是矩形。
(2)若 $AB = 2$,$\angle ACB = 30^{\circ}$,求 $BC$ 的长。
(1)证明: $\because \angle ACB=\angle DBC,\therefore BO=CO$. $\because$ 四边形 $ABCD$ 是平行四边形, $\therefore AC=2OC,BD=2OB$. $\therefore AC=BD$. $\therefore$ 平行四边形 $ABCD$ 是矩形.
(2) $\because$ 在矩形 $ABCD$ 中, $\angle ABC=90^{\circ},\therefore \triangle ABC$ 是直角三角形. $\because \angle ACB=30^{\circ},\therefore AC=2AB=2× 2=4$. $\therefore BC=\sqrt{AC^{2}-AB^{2}}=\sqrt{4^{2}-2^{2}}=$
$2\sqrt{3}$
.
答案:
解:
(1) 证明: $\because \angle ACB=\angle DBC,\therefore BO=CO$. $\because$ 四边形 $ABCD$ 是平行四边形, $\therefore AC=2OC,BD=2OB$. $\therefore AC=BD$. $\therefore$ 平行四边形 $ABCD$ 是矩形.
(2) $\because$ 在矩形 $ABCD$ 中, $\angle ABC=90^{\circ},\therefore \triangle ABC$ 是直角三角形. $\because \angle ACB=30^{\circ},\therefore AC=2AB=2\times 2=4$. $\therefore BC=\sqrt{AC^{2}-AB^{2}}=\sqrt{4^{2}-2^{2}}=2\sqrt{3}$.
(1) 证明: $\because \angle ACB=\angle DBC,\therefore BO=CO$. $\because$ 四边形 $ABCD$ 是平行四边形, $\therefore AC=2OC,BD=2OB$. $\therefore AC=BD$. $\therefore$ 平行四边形 $ABCD$ 是矩形.
(2) $\because$ 在矩形 $ABCD$ 中, $\angle ABC=90^{\circ},\therefore \triangle ABC$ 是直角三角形. $\because \angle ACB=30^{\circ},\therefore AC=2AB=2\times 2=4$. $\therefore BC=\sqrt{AC^{2}-AB^{2}}=\sqrt{4^{2}-2^{2}}=2\sqrt{3}$.
7. 如图,菱形 $ABCD$ 的对角线 $AC$,$BD$ 相交于点 $O$,$BE// AC$,$AE// BD$,$OE$ 与 $AB$ 交于点 $F$。
(1)求证:四边形 $AEBO$ 为矩形。
(2)若 $OE = 10$,$AC = 16$,求菱形 $ABCD$ 的面积。
解: (1) 证明: $\because BE// AC,AE// BD,\therefore$ 四边形 $AEBO$ 是平行四边形. 又 $\because$ 菱形 $ABCD$ 的对角线交于点 $O,\therefore AC\perp BD$. $\therefore \angle AOB=90^{\circ}$. $\therefore$ 平行四边形 $AEBO$ 为矩形. (2) $\because$ 四边形 $ABCD$ 是菱形, $AC=16,\therefore OA=\frac{1}{2}AC=8,OB=OD,AC\perp BD$. $\because$ 四边形 $AEBO$ 是矩形, $\therefore AB=OE=10$. $\therefore OB=\sqrt{AB^{2}-OA^{2}}=\sqrt{10^{2}-8^{2}}=6$. $\therefore BD=2OB=12$. $\therefore S_{菱形ABCD}=\frac{1}{2}AC\cdot BD=\frac{1}{2}× 16× 12=$
(1)求证:四边形 $AEBO$ 为矩形。
(2)若 $OE = 10$,$AC = 16$,求菱形 $ABCD$ 的面积。
解: (1) 证明: $\because BE// AC,AE// BD,\therefore$ 四边形 $AEBO$ 是平行四边形. 又 $\because$ 菱形 $ABCD$ 的对角线交于点 $O,\therefore AC\perp BD$. $\therefore \angle AOB=90^{\circ}$. $\therefore$ 平行四边形 $AEBO$ 为矩形. (2) $\because$ 四边形 $ABCD$ 是菱形, $AC=16,\therefore OA=\frac{1}{2}AC=8,OB=OD,AC\perp BD$. $\because$ 四边形 $AEBO$ 是矩形, $\therefore AB=OE=10$. $\therefore OB=\sqrt{AB^{2}-OA^{2}}=\sqrt{10^{2}-8^{2}}=6$. $\therefore BD=2OB=12$. $\therefore S_{菱形ABCD}=\frac{1}{2}AC\cdot BD=\frac{1}{2}× 16× 12=$
96
.
答案:
解:
(1) 证明: $\because BE// AC,AE// BD,\therefore$ 四边形 $AEBO$ 是平行四边形. 又 $\because$ 菱形 $ABCD$ 的对角线交于点 $O,\therefore AC\perp BD$. $\therefore \angle AOB=90^{\circ}$. $\therefore$ 平行四边形 $AEBO$ 为矩形.
(2) $\because$ 四边形 $ABCD$ 是菱形, $AC=16,\therefore OA=\frac{1}{2}AC=8,OB=OD,AC\perp BD$. $\because$ 四边形 $AEBO$ 是矩形, $\therefore AB=OE=10$. $\therefore OB=\sqrt{AB^{2}-OA^{2}}=\sqrt{10^{2}-8^{2}}=6$. $\therefore BD=2OB=12$. $\therefore S_{菱形ABCD}=\frac{1}{2}AC\cdot BD=\frac{1}{2}\times 16\times 12=96$.
(1) 证明: $\because BE// AC,AE// BD,\therefore$ 四边形 $AEBO$ 是平行四边形. 又 $\because$ 菱形 $ABCD$ 的对角线交于点 $O,\therefore AC\perp BD$. $\therefore \angle AOB=90^{\circ}$. $\therefore$ 平行四边形 $AEBO$ 为矩形.
(2) $\because$ 四边形 $ABCD$ 是菱形, $AC=16,\therefore OA=\frac{1}{2}AC=8,OB=OD,AC\perp BD$. $\because$ 四边形 $AEBO$ 是矩形, $\therefore AB=OE=10$. $\therefore OB=\sqrt{AB^{2}-OA^{2}}=\sqrt{10^{2}-8^{2}}=6$. $\therefore BD=2OB=12$. $\therefore S_{菱形ABCD}=\frac{1}{2}AC\cdot BD=\frac{1}{2}\times 16\times 12=96$.
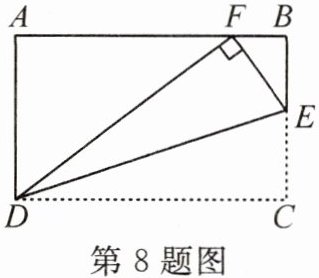
8. 如图,在矩形 $ABCD$ 中,$AB = 5$,$AD = 3$,$E$ 为 $BC$ 上一点,把 $\triangle CDE$ 沿 $DE$ 翻折,点 $C$ 恰好落在边 $AB$ 上的点 $F$ 处,则 $CE$ 的长是(
A. $1$
B. $\frac{4}{3}$
C. $\frac{3}{2}$
D. $\frac{5}{3}$
D
)
A. $1$
B. $\frac{4}{3}$
C. $\frac{3}{2}$
D. $\frac{5}{3}$
答案:
D
查看更多完整答案,请扫码查看


