第47页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
14. (2024·内江)已知关于x的一元二次方程$x^{2}-px+1= 0$(p为常数)有两个不相等的实数根$x_{1}和x_{2}$.
(1)填空:$x_{1}+x_{2}=$
(2)求$\frac {1}{x_{1}}+\frac {1}{x_{2}},x_{1}+\frac {1}{x_{1}}$的值.
(3)已知$x_{1}^{2}+x_{2}^{2}= 2p+1$,求p的值.
(2)由(1),得$x_1 + x_2 = p$,$x_1x_2 = 1$,∴$\frac{1}{x_1} + \frac{1}{x_2} = \frac{x_2 + x_1}{x_1x_2} = \frac{p}{1} = p$。∵关于$x$的一元二次方程$x^2 - px + 1 = 0$($p$为常数)有两个不相等的实数根$x_1$和$x_2$,∴$x_1^2 - px_1 + 1 = 0$。∴$x_1 - p + \frac{1}{x_1} = 0$,即$x_1 + \frac{1}{x_1} = p$。
(3)由(1),得$x_1 + x_2 = p$,$x_1x_2 = 1$,∵$x_1^2 + x_2^2 = 2p + 1$,∴$(x_1 + x_2)^2 - 2x_1x_2 = 2p + 1$。∴$p^2 - 2 = 2p + 1$,解得$p_1 = 3$,$p_2 = -1$。当$p = 3$时,$\Delta = p^2 - 4 = 9 - 4 = 5 > 0$;当$p = -1$时,$\Delta = p^2 - 4 = -3 < 0$(不合题意,舍去)。∴$p = 3$。
(1)填空:$x_{1}+x_{2}=$
p
,$x_{1}x_{2}=$1
.(2)求$\frac {1}{x_{1}}+\frac {1}{x_{2}},x_{1}+\frac {1}{x_{1}}$的值.
(3)已知$x_{1}^{2}+x_{2}^{2}= 2p+1$,求p的值.
(2)由(1),得$x_1 + x_2 = p$,$x_1x_2 = 1$,∴$\frac{1}{x_1} + \frac{1}{x_2} = \frac{x_2 + x_1}{x_1x_2} = \frac{p}{1} = p$。∵关于$x$的一元二次方程$x^2 - px + 1 = 0$($p$为常数)有两个不相等的实数根$x_1$和$x_2$,∴$x_1^2 - px_1 + 1 = 0$。∴$x_1 - p + \frac{1}{x_1} = 0$,即$x_1 + \frac{1}{x_1} = p$。
(3)由(1),得$x_1 + x_2 = p$,$x_1x_2 = 1$,∵$x_1^2 + x_2^2 = 2p + 1$,∴$(x_1 + x_2)^2 - 2x_1x_2 = 2p + 1$。∴$p^2 - 2 = 2p + 1$,解得$p_1 = 3$,$p_2 = -1$。当$p = 3$时,$\Delta = p^2 - 4 = 9 - 4 = 5 > 0$;当$p = -1$时,$\Delta = p^2 - 4 = -3 < 0$(不合题意,舍去)。∴$p = 3$。
答案:
解:
(1) $ p $ 1
(2) 由
(1),得 $ x_1 + x_2 = p $,$ x_1x_2 = 1 $,
∴ $ \frac{1}{x_1} + \frac{1}{x_2} = \frac{x_2 + x_1}{x_1x_2} = \frac{p}{1} = p $。
∵ 关于 $ x $ 的一元二次方程 $ x^2 - px + 1 = 0 $($ p $ 为常数)有两个不相等的实数根 $ x_1 $ 和 $ x_2 $,
∴ $ x_1^2 - px_1 + 1 = 0 $。
∴ $ x_1 - p + \frac{1}{x_1} = 0 $,即 $ x_1 + \frac{1}{x_1} = p $。
(3) 由
(1),得 $ x_1 + x_2 = p $,$ x_1x_2 = 1 $,
∵ $ x_1^2 + x_2^2 = 2p + 1 $,
∴ $ (x_1 + x_2)^2 - 2x_1x_2 = 2p + 1 $。
∴ $ p^2 - 2 = 2p + 1 $,解得 $ p_1 = 3 $,$ p_2 = -1 $。当 $ p = 3 $ 时,$ \Delta = p^2 - 4 = 9 - 4 = 5 > 0 $;当 $ p = -1 $ 时,$ \Delta = p^2 - 4 = -3 < 0 $(不合题意,舍去)。
∴ $ p = 3 $。
(1) $ p $ 1
(2) 由
(1),得 $ x_1 + x_2 = p $,$ x_1x_2 = 1 $,
∴ $ \frac{1}{x_1} + \frac{1}{x_2} = \frac{x_2 + x_1}{x_1x_2} = \frac{p}{1} = p $。
∵ 关于 $ x $ 的一元二次方程 $ x^2 - px + 1 = 0 $($ p $ 为常数)有两个不相等的实数根 $ x_1 $ 和 $ x_2 $,
∴ $ x_1^2 - px_1 + 1 = 0 $。
∴ $ x_1 - p + \frac{1}{x_1} = 0 $,即 $ x_1 + \frac{1}{x_1} = p $。
(3) 由
(1),得 $ x_1 + x_2 = p $,$ x_1x_2 = 1 $,
∵ $ x_1^2 + x_2^2 = 2p + 1 $,
∴ $ (x_1 + x_2)^2 - 2x_1x_2 = 2p + 1 $。
∴ $ p^2 - 2 = 2p + 1 $,解得 $ p_1 = 3 $,$ p_2 = -1 $。当 $ p = 3 $ 时,$ \Delta = p^2 - 4 = 9 - 4 = 5 > 0 $;当 $ p = -1 $ 时,$ \Delta = p^2 - 4 = -3 < 0 $(不合题意,舍去)。
∴ $ p = 3 $。
15. 新考向 数学文化 我国古代数学著作《增删算法统宗》记载“圆中方形”问题:“今有圆田一段,中间有个方池,丈量田地待耕犁,恰好三分在记,池面至周有数,每边三步无疑,内方圆径若能知,堪作算中第一.”其大意为:有一块圆形的田,中间有一块正方形水池,测量出除水池外圆内可耕地的面积恰好72平方步,从水池边到圆周,每边相距3步远.若设正方形的边长是x步,则列出的方程是 (
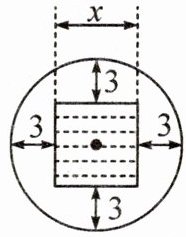
A. $π(x+3)^{2}-x^{2}= 72$
B. $π(\frac {x}{2}+3)^{2}-x^{2}= 72$
C. $π(x+3)^{2}-x^{2}= 36$
D. $π(\frac {x}{2}+3)^{2}-x^{2}= 36$
B
)
A. $π(x+3)^{2}-x^{2}= 72$
B. $π(\frac {x}{2}+3)^{2}-x^{2}= 72$
C. $π(x+3)^{2}-x^{2}= 36$
D. $π(\frac {x}{2}+3)^{2}-x^{2}= 36$
答案:
B
16. (2024·重庆)随着经济复苏,某公司近两年的总收入逐年递增.该公司2021年缴税40万元,2023年缴税48.4万元.该公司这两年缴税的年平均增长率是
10%
.
答案:
10%
17. (2024·辽宁)某商场出售一种商品,经市场调查发现,日销售量y(件)与每件售价x(元)之间满足一次函数关系,部分数据如表所示:

(1)求y与x之间的函数关系式(不要求写出自变量x的取值范围).
(2)该商品日销售额能否达到2600元? 如果能,求出每件售价;如果不能,说明理由.

(1)求y与x之间的函数关系式(不要求写出自变量x的取值范围).
y=-x+100
(2)该商品日销售额能否达到2600元? 如果能,求出每件售价;如果不能,说明理由.
不能,理由:设日销售额为w元,w=x(-x+100)=-x²+100x,令w=2600,得-x²+100x=2600,即x²-100x+2600=0,Δ=(-100)²-4×1×2600=10000-10400=-400<0,方程无实数根,所以不能达到2600元
答案:
解:
(1) 设 $ y $ 与 $ x $ 之间的函数关系式为 $ y = kx + b $,将 $ (45, 55) $,$ (55, 45) $ 代入,得 $ \begin{cases} 45k + b = 55 \\ 55k + b = 45 \end{cases} $,解得 $ \begin{cases} k = -1 \\ b = 100 \end{cases} $。
∴ $ y $ 与 $ x $ 之间的函数关系式为 $ y = -x + 100 $。
(2) 日销售额 $ w = x(-x + 100) = -x^2 + 100x $,又
∵ 日销售额是 2 600 元,
∴ $ 2 600 = -x^2 + 100x $。
∴ $ x^2 - 100x + 2 600 = 0 $。
∴ $ \Delta = (-100)^2 - 4 \times 2 600 = 10 000 - 10 400 = -400 < 0 $。
∴ 方程没有实数根,故该商品日销售额不能达到 2 600 元。
(1) 设 $ y $ 与 $ x $ 之间的函数关系式为 $ y = kx + b $,将 $ (45, 55) $,$ (55, 45) $ 代入,得 $ \begin{cases} 45k + b = 55 \\ 55k + b = 45 \end{cases} $,解得 $ \begin{cases} k = -1 \\ b = 100 \end{cases} $。
∴ $ y $ 与 $ x $ 之间的函数关系式为 $ y = -x + 100 $。
(2) 日销售额 $ w = x(-x + 100) = -x^2 + 100x $,又
∵ 日销售额是 2 600 元,
∴ $ 2 600 = -x^2 + 100x $。
∴ $ x^2 - 100x + 2 600 = 0 $。
∴ $ \Delta = (-100)^2 - 4 \times 2 600 = 10 000 - 10 400 = -400 < 0 $。
∴ 方程没有实数根,故该商品日销售额不能达到 2 600 元。
18. 定义:$[x]$表示不超过实数x的最大整数,例如:$[1.4]= 1,[-1.2]= -2,[-3]= -3$,则方程$2[x]= x^{2}$的解为
$x = 0$或$x = 2$或$x = \sqrt{2}$
。
答案:
解:
∵ $ x^2 \geq 0 $,$ 2[x] = x^2 $,
∴ $ x \geq 0 $。① 当 $ 0 \leq x < 1 $ 时,$ x^2 = 0 $,解得 $ x = 0 $;② 当 $ 1 \leq x < 2 $ 时,$ x^2 = 2 $,解得 $ x = \sqrt{2} $ 或 $ x = -\sqrt{2} $(舍去);③ 当 $ 2 \leq x < 3 $ 时,$ x^2 = 4 $,解得 $ x = 2 $ 或 $ x = -2 $(舍去);④ 当 $ x \geq 3 $ 时,方程无解。综上所述,方程 $ 2[x] = x^2 $ 的解为 $ x = 0 $ 或 $ x = 2 $ 或 $ x = \sqrt{2} $。
∵ $ x^2 \geq 0 $,$ 2[x] = x^2 $,
∴ $ x \geq 0 $。① 当 $ 0 \leq x < 1 $ 时,$ x^2 = 0 $,解得 $ x = 0 $;② 当 $ 1 \leq x < 2 $ 时,$ x^2 = 2 $,解得 $ x = \sqrt{2} $ 或 $ x = -\sqrt{2} $(舍去);③ 当 $ 2 \leq x < 3 $ 时,$ x^2 = 4 $,解得 $ x = 2 $ 或 $ x = -2 $(舍去);④ 当 $ x \geq 3 $ 时,方程无解。综上所述,方程 $ 2[x] = x^2 $ 的解为 $ x = 0 $ 或 $ x = 2 $ 或 $ x = \sqrt{2} $。
查看更多完整答案,请扫码查看


