第48页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
新考向 阅读理解 阅读材料,并解决问题.
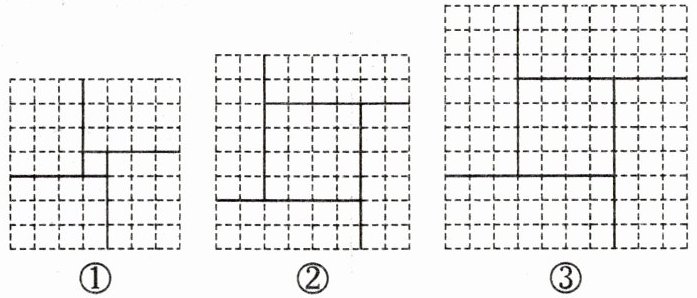
【学习研究】我国古代数学家赵爽在其所著的《勾股圆方图注》中记载了一元二次方程的几何解法,以$x^{2}+2x-35= 0$为例,构造方法如下:
首先将方程$x^{2}+2x-35= 0$变形为$x(x+2)= 35$,然后画四个长为$x+2$,宽为$x$的矩形,按如图1所示的方式拼成一个“空心”大正方形,则图1中大正方形的面积可表示为$(x+x+2)^{2}$,还可表示为四个矩形与一个边长为2的小正方形的面积之和,即$4x(x+2)+2^{2}= 4×35+4$.因此,可得新方程$(x+x+2)^{2}= 144$.因为$x$表示边长,所以$2x+2= 12$,即$x= 5$.遗憾的是,这样的做法只能得到方程的其中一个正根.
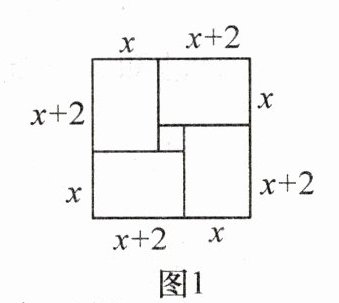
【理解应用】参照上述图解一元二次方程的方法,请在下面三个构图中选择能够用几何法求解方程$x^{2}-4x-12= 0(x>0)$的正确构图是(
【类比迁移】小颖根据以上解法解方程$2x^{2}+3x-2= 0$,请将其解答过程补充完整:
第一步:将原方程变形为$x^{2}+\frac {3}{2}x-1= 0$,即$x$
第二步:利用四个全等的矩形构造“空心”大正方形;
第三步:根据大正方形的面积可得新的方程
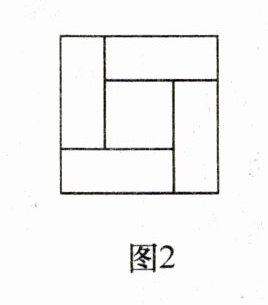
【拓展应用】一般地,对于形如$x^{2}+ax= b$的一元二次方程可以构造图2来解.已知图2是由四个面积为3的相同矩形构成,中间围成的正方形面积为4,那么此方程的系数$a=$
求得方程的正根为
【学习研究】我国古代数学家赵爽在其所著的《勾股圆方图注》中记载了一元二次方程的几何解法,以$x^{2}+2x-35= 0$为例,构造方法如下:
首先将方程$x^{2}+2x-35= 0$变形为$x(x+2)= 35$,然后画四个长为$x+2$,宽为$x$的矩形,按如图1所示的方式拼成一个“空心”大正方形,则图1中大正方形的面积可表示为$(x+x+2)^{2}$,还可表示为四个矩形与一个边长为2的小正方形的面积之和,即$4x(x+2)+2^{2}= 4×35+4$.因此,可得新方程$(x+x+2)^{2}= 144$.因为$x$表示边长,所以$2x+2= 12$,即$x= 5$.遗憾的是,这样的做法只能得到方程的其中一个正根.

【理解应用】参照上述图解一元二次方程的方法,请在下面三个构图中选择能够用几何法求解方程$x^{2}-4x-12= 0(x>0)$的正确构图是(
②
).(填序号)
【类比迁移】小颖根据以上解法解方程$2x^{2}+3x-2= 0$,请将其解答过程补充完整:
第一步:将原方程变形为$x^{2}+\frac {3}{2}x-1= 0$,即$x$
$(x+\frac {3}{2})=1$
;第二步:利用四个全等的矩形构造“空心”大正方形;
第三步:根据大正方形的面积可得新的方程
$(x+x+\frac {3}{2})^{2}=4×1+(\frac {3}{2})^{2}$
,解得原方程的一个根为$\frac {1}{2}$
.【拓展应用】一般地,对于形如$x^{2}+ax= b$的一元二次方程可以构造图2来解.已知图2是由四个面积为3的相同矩形构成,中间围成的正方形面积为4,那么此方程的系数$a=$
2(或-2)
,$b=$3
,
求得方程的正根为
1(或 3)
.
答案:
【理解应用】 ② 【类比迁移】 $(x+\frac {3}{2})=1$ $(x+x+\frac {3}{2})^{2}=4×1+(\frac {3}{2})^{2}$ $\frac {1}{2}$ 【拓展应用】 2(或-2) 3 1(或 3)
查看更多完整答案,请扫码查看


