第21页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
6. 如图,在正方形$ABCD$中,点$E在边CD$上,过点$B作BF⊥BE$,交$DA的延长线于点F$,作$∠CBF的平分线BP$,交边$AD于点P$.
(1)根据题意,补全图形(画图工具不限).
(2)求证:$BE= BF$.
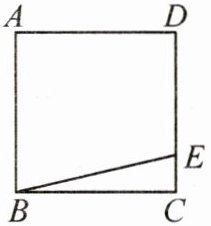
(3)若$AB= 3,CE= 1$,求$AP$的长.
(1) 图略. (2) 证明: $\because$ 四边形 $ABCD$ 是正方形, $\therefore ∠ABC = ∠C = ∠BAD = 90^{\circ}$, $AB = BC$. $\therefore ∠ABE + ∠CBE = 90^{\circ}$. $\because BF \perp BE$, $\therefore ∠FBE = ∠ABF + ∠ABE = 90^{\circ}$. $\therefore ∠ABF = ∠CBE$. $\because ∠BAD + ∠BAF = 180^{\circ}$, $\therefore ∠BAF = 90^{\circ}$. $\therefore ∠BAF = ∠C = 90^{\circ}$. $\therefore △CBE \cong △ABF(ASA)$. $\therefore BE = BF$. (3) 在 $Rt△EBC$ 中, $BC = AB = 3$, $CE = 1$, $\therefore BE = \sqrt{CE^{2} + BC^{2}} = \sqrt{10}$. 由 (2) 得, $BF = BE = \sqrt{10}$. $\because BP$ 平分 $∠CBF$, $\therefore ∠PBC = ∠PBF$. $\because AD // BC$, $\therefore ∠BPF = ∠PBC$. $\therefore ∠BPF = ∠PBF$. $\therefore PF = BF = \sqrt{10}$. 由 (2) 得, $△CBE \cong △ABF$, $\therefore AF = CE = 1$. $\therefore AP = PF - AF =$
(1)根据题意,补全图形(画图工具不限).
(2)求证:$BE= BF$.

(3)若$AB= 3,CE= 1$,求$AP$的长.
(1) 图略. (2) 证明: $\because$ 四边形 $ABCD$ 是正方形, $\therefore ∠ABC = ∠C = ∠BAD = 90^{\circ}$, $AB = BC$. $\therefore ∠ABE + ∠CBE = 90^{\circ}$. $\because BF \perp BE$, $\therefore ∠FBE = ∠ABF + ∠ABE = 90^{\circ}$. $\therefore ∠ABF = ∠CBE$. $\because ∠BAD + ∠BAF = 180^{\circ}$, $\therefore ∠BAF = 90^{\circ}$. $\therefore ∠BAF = ∠C = 90^{\circ}$. $\therefore △CBE \cong △ABF(ASA)$. $\therefore BE = BF$. (3) 在 $Rt△EBC$ 中, $BC = AB = 3$, $CE = 1$, $\therefore BE = \sqrt{CE^{2} + BC^{2}} = \sqrt{10}$. 由 (2) 得, $BF = BE = \sqrt{10}$. $\because BP$ 平分 $∠CBF$, $\therefore ∠PBC = ∠PBF$. $\because AD // BC$, $\therefore ∠BPF = ∠PBC$. $\therefore ∠BPF = ∠PBF$. $\therefore PF = BF = \sqrt{10}$. 由 (2) 得, $△CBE \cong △ABF$, $\therefore AF = CE = 1$. $\therefore AP = PF - AF =$
$\sqrt{10} - 1$
.
答案:
解:
(1) 图略.
(2) 证明: $\because$ 四边形 $ABCD$ 是正方形, $\therefore ∠ABC = ∠C = ∠BAD = 90^{\circ}$, $AB = BC$. $\therefore ∠ABE + ∠CBE = 90^{\circ}$. $\because BF \perp BE$, $\therefore ∠FBE = ∠ABF + ∠ABE = 90^{\circ}$. $\therefore ∠ABF = ∠CBE$. $\because ∠BAD + ∠BAF = 180^{\circ}$, $\therefore ∠BAF = 90^{\circ}$. $\therefore ∠BAF = ∠C = 90^{\circ}$. $\therefore △CBE \cong △ABF(ASA)$. $\therefore BE = BF$.
(3) 在 $Rt△EBC$ 中, $BC = AB = 3$, $CE = 1$, $\therefore BE = \sqrt{CE^{2} + BC^{2}} = \sqrt{10}$. 由
(2) 得, $BF = BE = \sqrt{10}$. $\because BP$ 平分 $∠CBF$, $\therefore ∠PBC = ∠PBF$. $\because AD // BC$, $\therefore ∠BPF = ∠PBC$. $\therefore ∠BPF = ∠PBF$. $\therefore PF = BF = \sqrt{10}$. 由
(2) 得, $△CBE \cong △ABF$, $\therefore AF = CE = 1$. $\therefore AP = PF - AF = \sqrt{10} - 1$.
(1) 图略.
(2) 证明: $\because$ 四边形 $ABCD$ 是正方形, $\therefore ∠ABC = ∠C = ∠BAD = 90^{\circ}$, $AB = BC$. $\therefore ∠ABE + ∠CBE = 90^{\circ}$. $\because BF \perp BE$, $\therefore ∠FBE = ∠ABF + ∠ABE = 90^{\circ}$. $\therefore ∠ABF = ∠CBE$. $\because ∠BAD + ∠BAF = 180^{\circ}$, $\therefore ∠BAF = 90^{\circ}$. $\therefore ∠BAF = ∠C = 90^{\circ}$. $\therefore △CBE \cong △ABF(ASA)$. $\therefore BE = BF$.
(3) 在 $Rt△EBC$ 中, $BC = AB = 3$, $CE = 1$, $\therefore BE = \sqrt{CE^{2} + BC^{2}} = \sqrt{10}$. 由
(2) 得, $BF = BE = \sqrt{10}$. $\because BP$ 平分 $∠CBF$, $\therefore ∠PBC = ∠PBF$. $\because AD // BC$, $\therefore ∠BPF = ∠PBC$. $\therefore ∠BPF = ∠PBF$. $\therefore PF = BF = \sqrt{10}$. 由
(2) 得, $△CBE \cong △ABF$, $\therefore AF = CE = 1$. $\therefore AP = PF - AF = \sqrt{10} - 1$.
如图在△ABC中,AB=AC,P为BC上任意一点,$PE⊥AB于点E$,$PF⊥AC于点F$,$BM⊥AC于点M$. 求证:$PE+PF= BM$.
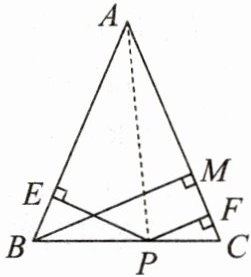
证明:连接$AP$.
$\because PE⊥AB,PF⊥AC,BM⊥AC$,
$\therefore S_{△ABP}=$
$\because$
$\therefore \frac {1}{2}AB\cdot PE+\frac {1}{2}AC\cdot PF= \frac {1}{2}AC\cdot BM$.
$\because AB= AC,\therefore PE+PF= BM$.
结论:等腰三角形底边上任意一点到两腰的距离之和等于一腰上的高.

证明:连接$AP$.
$\because PE⊥AB,PF⊥AC,BM⊥AC$,
$\therefore S_{△ABP}=$
$\frac{1}{2}AB\cdot PE$
,$S_{△ACP}=$$\frac{1}{2}AC\cdot PF$
,$S_{△ABC}=$$\frac{1}{2}AC\cdot BM$
.$\because$
$S_{\triangle ABP}$
+$S_{\triangle ACP}$
$=S_{△ABC}$,$\therefore \frac {1}{2}AB\cdot PE+\frac {1}{2}AC\cdot PF= \frac {1}{2}AC\cdot BM$.
$\because AB= AC,\therefore PE+PF= BM$.
结论:等腰三角形底边上任意一点到两腰的距离之和等于一腰上的高.
答案:
1. 首先根据三角形面积公式$S = \frac{1}{2}ah$($a$为底,$h$为高):
因为$PE\perp AB$,所以$S_{\triangle ABP}=\frac{1}{2}AB\cdot PE$(这里$AB$为底,$PE$为高);
因为$PF\perp AC$,所以$S_{\triangle ACP}=\frac{1}{2}AC\cdot PF$(这里$AC$为底,$PF$为高);
因为$BM\perp AC$,所以$S_{\triangle ABC}=\frac{1}{2}AC\cdot BM$(这里$AC$为底,$BM$为高)。
2. 然后根据图形的面积关系:
因为$S_{\triangle ABP}+S_{\triangle ACP}=S_{\triangle ABC}$($\triangle ABC$的面积等于$\triangle ABP$与$\triangle ACP$的面积之和)。
故答案依次为:$\frac{1}{2}AB\cdot PE$;$\frac{1}{2}AC\cdot PF$;$\frac{1}{2}AC\cdot BM$;$S_{\triangle ABP}$;$S_{\triangle ACP}$。
因为$PE\perp AB$,所以$S_{\triangle ABP}=\frac{1}{2}AB\cdot PE$(这里$AB$为底,$PE$为高);
因为$PF\perp AC$,所以$S_{\triangle ACP}=\frac{1}{2}AC\cdot PF$(这里$AC$为底,$PF$为高);
因为$BM\perp AC$,所以$S_{\triangle ABC}=\frac{1}{2}AC\cdot BM$(这里$AC$为底,$BM$为高)。
2. 然后根据图形的面积关系:
因为$S_{\triangle ABP}+S_{\triangle ACP}=S_{\triangle ABC}$($\triangle ABC$的面积等于$\triangle ABP$与$\triangle ACP$的面积之和)。
故答案依次为:$\frac{1}{2}AB\cdot PE$;$\frac{1}{2}AC\cdot PF$;$\frac{1}{2}AC\cdot BM$;$S_{\triangle ABP}$;$S_{\triangle ACP}$。
1. 新考向 传统文化
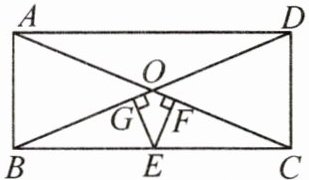
(2023·内江)出入相补原理是我国古代数学的重要成就之一,最早是由魏晋时期数学家刘徽创建.“将一个几何图形任意切成多块小图形,几何图形的总面积保持不变,等于所分割的小图形的面积之和”是该原理的重要内容之一. 如图,在矩形$ABCD$中,$AB= 5$,$AD= 12$,对角线$AC与BD相交于点O$,$E为边BC$上的一个动点,$EF⊥AC$,$EG⊥BD$,垂足分别为$F$,$G$,则$EF+EG= $

(2023·内江)出入相补原理是我国古代数学的重要成就之一,最早是由魏晋时期数学家刘徽创建.“将一个几何图形任意切成多块小图形,几何图形的总面积保持不变,等于所分割的小图形的面积之和”是该原理的重要内容之一. 如图,在矩形$ABCD$中,$AB= 5$,$AD= 12$,对角线$AC与BD相交于点O$,$E为边BC$上的一个动点,$EF⊥AC$,$EG⊥BD$,垂足分别为$F$,$G$,则$EF+EG= $
$\frac{60}{13}$
.
答案:
$\frac{60}{13}$
1. 新考向 传统文化

(2023·内江)出入相补原理是我国古代数学的重要成就之一,最早是由魏晋时期数学家刘徽创建.“将一个几何图形任意切成多块小图形,几何图形的总面积保持不变,等于所分割的小图形的面积之和”是该原理的重要内容之一. 如图,在矩形$ABCD$中,$AB= 5$,$AD= 12$,对角线$AC与BD相交于点O$,$E为边BC$上的一个动点,$EF⊥AC$,$EG⊥BD$,垂足分别为$F$,$G$,则$EF+EG= $

(2023·内江)出入相补原理是我国古代数学的重要成就之一,最早是由魏晋时期数学家刘徽创建.“将一个几何图形任意切成多块小图形,几何图形的总面积保持不变,等于所分割的小图形的面积之和”是该原理的重要内容之一. 如图,在矩形$ABCD$中,$AB= 5$,$AD= 12$,对角线$AC与BD相交于点O$,$E为边BC$上的一个动点,$EF⊥AC$,$EG⊥BD$,垂足分别为$F$,$G$,则$EF+EG= $
$\frac{60}{13}$
.
答案:
1. 首先求矩形$ABCD$的对角线$AC$的长度:
根据勾股定理$a^{2}+b^{2}=c^{2}$(在矩形$ABCD$中,$AB = a = 5$,$AD = b = 12$,$AC$为对角线$c$),则$AC=\sqrt{AB^{2}+AD^{2}}$。
把$AB = 5$,$AD = 12$代入可得$AC=\sqrt{5^{2}+12^{2}}=\sqrt{25 + 144}=\sqrt{169}=13$。
因为矩形的对角线相等且互相平分,所以$OB = OC=\frac{1}{2}AC=\frac{13}{2}$,$S_{\triangle BOC}=\frac{1}{4}S_{矩形ABCD}$。
又$S_{矩形ABCD}=AB× AD=5×12 = 60$,所以$S_{\triangle BOC}=\frac{1}{4}×60 = 15$。
2. 然后利用面积法:
连接$OE$,$S_{\triangle BOC}=S_{\triangle BOE}+S_{\triangle COE}$。
根据三角形面积公式$S=\frac{1}{2}ah$(对于$\triangle BOE$,$a = OB$,$h = EG$;对于$\triangle COE$,$a = OC$,$h = EF$)。
因为$OB = OC=\frac{13}{2}$,所以$S_{\triangle BOC}=\frac{1}{2}OB× EG+\frac{1}{2}OC× EF=\frac{1}{2}OC(EF + EG)$($OB = OC$)。
已知$S_{\triangle BOC}=15$,$OC=\frac{13}{2}$,将$S_{\triangle BOC}=15$,$OC=\frac{13}{2}$代入$S_{\triangle BOC}=\frac{1}{2}OC(EF + EG)$中,得$15=\frac{1}{2}×\frac{13}{2}(EF + EG)$。
则$EF + EG=\frac{15×2×2}{13}=\frac{60}{13}$。
故$EF + EG=\frac{60}{13}$。
根据勾股定理$a^{2}+b^{2}=c^{2}$(在矩形$ABCD$中,$AB = a = 5$,$AD = b = 12$,$AC$为对角线$c$),则$AC=\sqrt{AB^{2}+AD^{2}}$。
把$AB = 5$,$AD = 12$代入可得$AC=\sqrt{5^{2}+12^{2}}=\sqrt{25 + 144}=\sqrt{169}=13$。
因为矩形的对角线相等且互相平分,所以$OB = OC=\frac{1}{2}AC=\frac{13}{2}$,$S_{\triangle BOC}=\frac{1}{4}S_{矩形ABCD}$。
又$S_{矩形ABCD}=AB× AD=5×12 = 60$,所以$S_{\triangle BOC}=\frac{1}{4}×60 = 15$。
2. 然后利用面积法:
连接$OE$,$S_{\triangle BOC}=S_{\triangle BOE}+S_{\triangle COE}$。
根据三角形面积公式$S=\frac{1}{2}ah$(对于$\triangle BOE$,$a = OB$,$h = EG$;对于$\triangle COE$,$a = OC$,$h = EF$)。
因为$OB = OC=\frac{13}{2}$,所以$S_{\triangle BOC}=\frac{1}{2}OB× EG+\frac{1}{2}OC× EF=\frac{1}{2}OC(EF + EG)$($OB = OC$)。
已知$S_{\triangle BOC}=15$,$OC=\frac{13}{2}$,将$S_{\triangle BOC}=15$,$OC=\frac{13}{2}$代入$S_{\triangle BOC}=\frac{1}{2}OC(EF + EG)$中,得$15=\frac{1}{2}×\frac{13}{2}(EF + EG)$。
则$EF + EG=\frac{15×2×2}{13}=\frac{60}{13}$。
故$EF + EG=\frac{60}{13}$。
2. 如图,在菱形$ABCD$中,$P是对角线AC$上一动点,过点$P作PE⊥BC于点E$,$PF⊥AB于点F$. 若菱形$ABCD的周长为20$,面积为$24$,则$PE+PF$的值为____
$\frac{24}{5}$
.
答案:
1. 首先求菱形的边长:
已知菱形$ABCD$的周长为$20$,因为菱形的四条边相等,设边长为$a$,根据周长公式$C = 4a$,则$4a=20$,解得$a = 5$。
2. 然后连接$BP$:
因为$S_{\triangle ABC}+S_{\triangle ADC}=S_{菱形ABCD}$,且$S_{\triangle ABC}=S_{\triangle ADC}$(菱形的对角线平分菱形的面积),所以$S_{\triangle ABC}=\frac{1}{2}S_{菱形ABCD}$。
已知$S_{菱形ABCD}=24$,则$S_{\triangle ABC}=12$。
又因为$S_{\triangle ABC}=S_{\triangle ABP}+S_{\triangle BCP}$。
根据三角形面积公式$S=\frac{1}{2}ah$($a$为底,$h$为高),对于$S_{\triangle ABP}$,以$AB$为底,$PF$为高,$S_{\triangle ABP}=\frac{1}{2}AB\cdot PF$;对于$S_{\triangle BCP}$,以$BC$为底,$PE$为高,$S_{\triangle BCP}=\frac{1}{2}BC\cdot PE$。
因为$AB = BC=a = 5$。
所以$S_{\triangle ABC}=\frac{1}{2}AB\cdot PF+\frac{1}{2}BC\cdot PE$。
把$AB = BC = 5$,$S_{\triangle ABC}=12$代入上式得:$S_{\triangle ABC}=\frac{1}{2}(AB\cdot PF + BC\cdot PE)=\frac{1}{2}×5×(PE + PF)$。
3. 最后求解$PE + PF$的值:
由$\frac{1}{2}×5×(PE + PF)=12$。
则$PE + PF=\frac{24}{5}$。
故答案为$\frac{24}{5}$。
已知菱形$ABCD$的周长为$20$,因为菱形的四条边相等,设边长为$a$,根据周长公式$C = 4a$,则$4a=20$,解得$a = 5$。
2. 然后连接$BP$:
因为$S_{\triangle ABC}+S_{\triangle ADC}=S_{菱形ABCD}$,且$S_{\triangle ABC}=S_{\triangle ADC}$(菱形的对角线平分菱形的面积),所以$S_{\triangle ABC}=\frac{1}{2}S_{菱形ABCD}$。
已知$S_{菱形ABCD}=24$,则$S_{\triangle ABC}=12$。
又因为$S_{\triangle ABC}=S_{\triangle ABP}+S_{\triangle BCP}$。
根据三角形面积公式$S=\frac{1}{2}ah$($a$为底,$h$为高),对于$S_{\triangle ABP}$,以$AB$为底,$PF$为高,$S_{\triangle ABP}=\frac{1}{2}AB\cdot PF$;对于$S_{\triangle BCP}$,以$BC$为底,$PE$为高,$S_{\triangle BCP}=\frac{1}{2}BC\cdot PE$。
因为$AB = BC=a = 5$。
所以$S_{\triangle ABC}=\frac{1}{2}AB\cdot PF+\frac{1}{2}BC\cdot PE$。
把$AB = BC = 5$,$S_{\triangle ABC}=12$代入上式得:$S_{\triangle ABC}=\frac{1}{2}(AB\cdot PF + BC\cdot PE)=\frac{1}{2}×5×(PE + PF)$。
3. 最后求解$PE + PF$的值:
由$\frac{1}{2}×5×(PE + PF)=12$。
则$PE + PF=\frac{24}{5}$。
故答案为$\frac{24}{5}$。
3. 如图所示,$E是边长为1的正方形ABCD的对角线BD$上一点,且$BE= BC$,$P为CE$上任意一点,$PQ⊥BC于点Q$,$PR⊥BE于点R$,则$PQ+PR$的值是____
$\frac{\sqrt{2}}{2}$
.
答案:
1. 首先,连接$BP$:
已知正方形$ABCD$边长$BC = 1$,因为$BE = BC = 1$,且$\triangle BCE$的面积$S_{\triangle BCE}=S_{\triangle BCP}+S_{\triangle BEP}$。
根据三角形面积公式$S=\frac{1}{2}ah$($a$为底,$h$为高)。
对于$\triangle BCP$,以$BC$为底,$PQ$为高,则$S_{\triangle BCP}=\frac{1}{2}BC\cdot PQ$;对于$\triangle BEP$,以$BE$为底,$PR$为高,则$S_{\triangle BEP}=\frac{1}{2}BE\cdot PR$;对于$\triangle BCE$,因为正方形$ABCD$中$\angle DBC = 45^{\circ}$,$BE = BC = 1$,过$C$作$CM\perp BD$于$M$,在$Rt\triangle BCM$中,$\angle BCM = 45^{\circ}$,$\sin\angle DBC=\frac{CM}{BC}$,又$BC = 1$,$\angle DBC = 45^{\circ}$,所以$CM = BC\sin45^{\circ}=1×\frac{\sqrt{2}}{2}=\frac{\sqrt{2}}{2}$,则$S_{\triangle BCE}=\frac{1}{2}BE\cdot CM$。
2. 然后,根据面积关系:
因为$S_{\triangle BCE}=S_{\triangle BCP}+S_{\triangle BEP}$,$BE = BC$。
所以$\frac{1}{2}BE\cdot CM=\frac{1}{2}BC\cdot PQ+\frac{1}{2}BE\cdot PR$。
又$BE = BC$,等式两边同时除以$\frac{1}{2}BC$($BC\neq0$),可得$CM = PQ + PR$。
所以$PQ + PR=\frac{\sqrt{2}}{2}$。
故答案为$\frac{\sqrt{2}}{2}$。
已知正方形$ABCD$边长$BC = 1$,因为$BE = BC = 1$,且$\triangle BCE$的面积$S_{\triangle BCE}=S_{\triangle BCP}+S_{\triangle BEP}$。
根据三角形面积公式$S=\frac{1}{2}ah$($a$为底,$h$为高)。
对于$\triangle BCP$,以$BC$为底,$PQ$为高,则$S_{\triangle BCP}=\frac{1}{2}BC\cdot PQ$;对于$\triangle BEP$,以$BE$为底,$PR$为高,则$S_{\triangle BEP}=\frac{1}{2}BE\cdot PR$;对于$\triangle BCE$,因为正方形$ABCD$中$\angle DBC = 45^{\circ}$,$BE = BC = 1$,过$C$作$CM\perp BD$于$M$,在$Rt\triangle BCM$中,$\angle BCM = 45^{\circ}$,$\sin\angle DBC=\frac{CM}{BC}$,又$BC = 1$,$\angle DBC = 45^{\circ}$,所以$CM = BC\sin45^{\circ}=1×\frac{\sqrt{2}}{2}=\frac{\sqrt{2}}{2}$,则$S_{\triangle BCE}=\frac{1}{2}BE\cdot CM$。
2. 然后,根据面积关系:
因为$S_{\triangle BCE}=S_{\triangle BCP}+S_{\triangle BEP}$,$BE = BC$。
所以$\frac{1}{2}BE\cdot CM=\frac{1}{2}BC\cdot PQ+\frac{1}{2}BE\cdot PR$。
又$BE = BC$,等式两边同时除以$\frac{1}{2}BC$($BC\neq0$),可得$CM = PQ + PR$。
所以$PQ + PR=\frac{\sqrt{2}}{2}$。
故答案为$\frac{\sqrt{2}}{2}$。
查看更多完整答案,请扫码查看


