第14页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
1. 菱形、矩形、正方形都具有的性质是(
A. 对角线互相垂直
B. 对角线相等
C. 对角线互相平分
D. 对角线平分对角
C
)A. 对角线互相垂直
B. 对角线相等
C. 对角线互相平分
D. 对角线平分对角
答案:
C
2. (2023·自贡)如图,边长为3的正方形OBCD两边与坐标轴正半轴重合,则点C的坐标是(
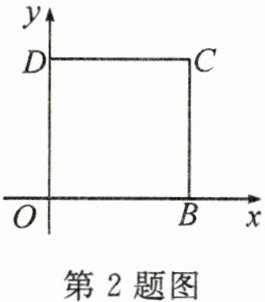
A. $(3,-3)$
B. $(-3,3)$
C. $(3,3)$
D. $(-3,-3)$
C
)
A. $(3,-3)$
B. $(-3,3)$
C. $(3,3)$
D. $(-3,-3)$
答案:
C
3. 如图,正方形ABCD的边长为1,E,F是对角线AC上的两点,$EG⊥AB,EI⊥AD,FH⊥AB,FJ⊥AD$,垂足分别为G,I,H,J,则图中阴影部分的面积等于(
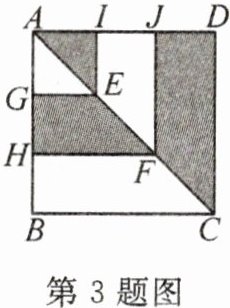
A. 1
B. $\frac{1}{2}$
C. $\frac{1}{3}$
D. $\frac{1}{4}$
B
)
A. 1
B. $\frac{1}{2}$
C. $\frac{1}{3}$
D. $\frac{1}{4}$
答案:
B
4. 新考向 传统文化 如图1所示的杜岭二号方鼎是河南博物院九大镇院之宝之一,方鼎的口呈正方形(如图2),正方形ABCD的对角线AC与BD相交于点O,则下列说法不正确的是(

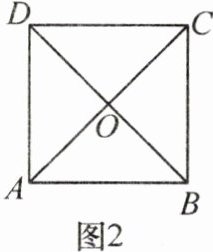
A. $AC⊥BD$
B. $AD= AO$
C. $DO= CO$
D. $∠DAO= ∠BAC$
B
)

A. $AC⊥BD$
B. $AD= AO$
C. $DO= CO$
D. $∠DAO= ∠BAC$
答案:
B
5. 如图,在正方形ABCD中,E,F分别是AB,AD的中点.若$EF= 2$,则AC的长是____

4
.
答案:
4
6. (2024·常州)如图,在平面直角坐标系xOy中,正方形ABCD的对角线AC,BD相交于原点O.若点A的坐标是$(2,1)$,则点C的坐标是

$(-2,-1)$
.
答案:
$(-2,-1)$
7. (2024·兰州)如图,四边形ABCD为正方形,$△ADE$为等边三角形,$EF⊥AB$于点F.若$AD= 4$,则$EF=$
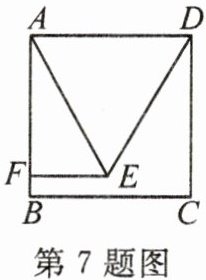
2
.
答案:
2
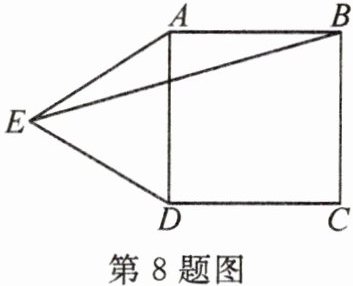
8. 如图,以AD为边在正方形ABCD的外侧作等边三角形ADE,则$∠BED=$
【拓展变式】 在正方形ABCD所在的平面内,以AD为边作等边三角形ADE,则$∠BED=$
$45^{\circ}$
.【拓展变式】 在正方形ABCD所在的平面内,以AD为边作等边三角形ADE,则$∠BED=$
$45^{\circ}$或$135^{\circ}$
.
答案:
$45^{\circ}$
【拓展变式】$45^{\circ}$或$135^{\circ}$
【拓展变式】$45^{\circ}$或$135^{\circ}$
9. 如图,在正方形ABCD中,点E在边BC的延长线上,点F在边CD的延长线上,且$CE= DF$,连接AE和BF相交于点M.求证:$AE= BF$.
证明:在正方形$ABCD$中,$AB = BC = CD = DA$,$\angle ABC=\angle BCD = 90^{\circ}$.$\because CE = DF$,$\therefore$
证明:在正方形$ABCD$中,$AB = BC = CD = DA$,$\angle ABC=\angle BCD = 90^{\circ}$.$\because CE = DF$,$\therefore$
$BE = CF$
.在$\triangle AEB$和$\triangle BFC$中,$\left\{\begin{array}{l} AB = BC,\\ \angle ABE = \angle BCF,\\ BE = CF,\end{array}\right.$$\therefore$$\triangle AEB\cong \triangle BFC(SAS)$
.$\therefore AE = BF$.
答案:
证明:在正方形$ABCD$中,$AB = BC = CD = DA$,$\angle ABC=\angle BCD = 90^{\circ}$.$\because CE = DF$,$\therefore BE = CF$.在$\triangle AEB$和$\triangle BFC$中,$\left\{\begin{array}{l} AB = BC,\\ \angle ABE = \angle BCF,\\ BE = CF,\end{array}\right.$$\therefore \triangle AEB\cong \triangle BFC(SAS)$.$\therefore AE = BF$.
10. 已知正方形ABCD的边长为6,如果P是正方形内一点,且$PB= PD= 2\sqrt{5}$,那么AP的长为
$4\sqrt {2}$或$2\sqrt {2}$
.
答案:
$4\sqrt {2}$或$2\sqrt {2}$
查看更多完整答案,请扫码查看


