第24页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
10. (2024·天津)如图,正方形ABCD的边长为$3\sqrt {2}$,对角线AC,BD相交于点O,点E在CA的延长线上,$OE= 5$,连接DE.
(1)线段AE的长为______
(2)若F为DE的中点,则线段AF的长为______

(1)线段AE的长为______
2
.(2)若F为DE的中点,则线段AF的长为______
$\frac{\sqrt{10}}{2}$
.
答案:
(1) 2
(2) $ \frac{\sqrt{10}}{2} $
(1) 2
(2) $ \frac{\sqrt{10}}{2} $
11. 如图1,在正方形ABCD中,点E,F分别在AB,BC上,且$AE= BF$.
(1)试探索线段AF,DE的数量关系,写出你的结论,并说明理由.
结论:
(2)连接EF,DF,分别取AE,EF,FD,DA的中点H,I,J,K,顺次连接,得到四边形HIJK.
①请在图2中补全图形.
②四边形HIJK是什么特殊平行四边形?请说明理由.
答:四边形HIJK是
(1)试探索线段AF,DE的数量关系,写出你的结论,并说明理由.
结论:
AF=DE
(2)连接EF,DF,分别取AE,EF,FD,DA的中点H,I,J,K,顺次连接,得到四边形HIJK.
①请在图2中补全图形.
②四边形HIJK是什么特殊平行四边形?请说明理由.
答:四边形HIJK是
正方形
答案:
解:
(1) $ AF = DE $. 理由如下: $ \because $ 四边形 $ ABCD $ 是正方形, $ \therefore AD = BA $, $ \angle DAE = \angle ABF = 90^{\circ} $. $ \because AE = BF $, $ \therefore \triangle DAE \cong \triangle ABF (SAS) $. $ \therefore AF = DE $.
(2) ① 图略. ② 四边形 $ HIJK $ 是正方形. 理由如下: $ \because H $, $ I $, $ J $, $ K $ 分别是 $ AE $, $ EF $, $ FD $, $ DA $ 的中点, $ \therefore HI = KJ = \frac{1}{2}AF $, $ HK = IJ = \frac{1}{2}ED $, $ HI // AF $, $ HK // DE $. $ \because AF = DE $, $ \therefore HI = KJ = HK = IJ $. $ \therefore $ 四边形 $ HIJK $ 是菱形. $ \because \triangle DAE \cong \triangle ABF $, $ \therefore \angle ADE = \angle BAF $. $ \because \angle ADE + \angle AED = 90^{\circ} $, $ \therefore \angle BAF + \angle AED = 90^{\circ} $. $ \therefore \angle AOE = 90^{\circ} $. 又 $ \because HI // AF $, $ HK // DE $, $ \therefore $ 易得 $ \angle KHI = 90^{\circ} $. $ \therefore $ 菱形 $ HIJK $ 是正方形.
(1) $ AF = DE $. 理由如下: $ \because $ 四边形 $ ABCD $ 是正方形, $ \therefore AD = BA $, $ \angle DAE = \angle ABF = 90^{\circ} $. $ \because AE = BF $, $ \therefore \triangle DAE \cong \triangle ABF (SAS) $. $ \therefore AF = DE $.
(2) ① 图略. ② 四边形 $ HIJK $ 是正方形. 理由如下: $ \because H $, $ I $, $ J $, $ K $ 分别是 $ AE $, $ EF $, $ FD $, $ DA $ 的中点, $ \therefore HI = KJ = \frac{1}{2}AF $, $ HK = IJ = \frac{1}{2}ED $, $ HI // AF $, $ HK // DE $. $ \because AF = DE $, $ \therefore HI = KJ = HK = IJ $. $ \therefore $ 四边形 $ HIJK $ 是菱形. $ \because \triangle DAE \cong \triangle ABF $, $ \therefore \angle ADE = \angle BAF $. $ \because \angle ADE + \angle AED = 90^{\circ} $, $ \therefore \angle BAF + \angle AED = 90^{\circ} $. $ \therefore \angle AOE = 90^{\circ} $. 又 $ \because HI // AF $, $ HK // DE $, $ \therefore $ 易得 $ \angle KHI = 90^{\circ} $. $ \therefore $ 菱形 $ HIJK $ 是正方形.
12. 综合与实践:
宽与长的比是$\frac {\sqrt {5}-1}{2}$(约为0.618)的矩形叫黄金矩形.黄金矩形给我们以协调、匀称的美感,世界各国许多著名的建筑,为取得最佳的视觉效果,都采用黄金矩形的设计,如希腊的帕特农神庙等.
实践操作:下面我们折叠出一个黄金矩形(如图所示).
第一步:在一张矩形纸片的一端,利用图1的方法折出一个正方形,然后把纸展平.
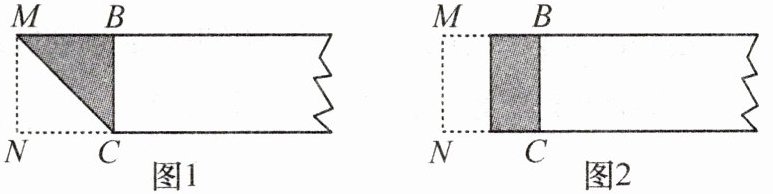
第二步:如图2,把这个正方形折成两个相等的矩形,再把纸片展平.
第三步:折出内侧矩形的对角线AB,并把AB折到如图3所示的AD处.
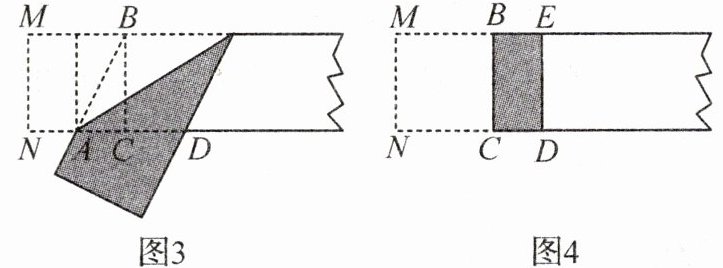
第四步:展平纸片,按照所得的点D折出DE,则矩形BCDE(图4)就是黄金矩形.
问题解决:
(1)请在图1中证明四边形MNCB是正方形.
(2)若$MN= 4$,请通过计算$\frac {BE}{BC}$的值来说明矩形BCDE是黄金矩形.
宽与长的比是$\frac {\sqrt {5}-1}{2}$(约为0.618)的矩形叫黄金矩形.黄金矩形给我们以协调、匀称的美感,世界各国许多著名的建筑,为取得最佳的视觉效果,都采用黄金矩形的设计,如希腊的帕特农神庙等.
实践操作:下面我们折叠出一个黄金矩形(如图所示).
第一步:在一张矩形纸片的一端,利用图1的方法折出一个正方形,然后把纸展平.

第二步:如图2,把这个正方形折成两个相等的矩形,再把纸片展平.
第三步:折出内侧矩形的对角线AB,并把AB折到如图3所示的AD处.

第四步:展平纸片,按照所得的点D折出DE,则矩形BCDE(图4)就是黄金矩形.
问题解决:
(1)请在图1中证明四边形MNCB是正方形.
(2)若$MN= 4$,请通过计算$\frac {BE}{BC}$的值来说明矩形BCDE是黄金矩形.
答案:
解:
(1) 证明: 由矩形的性质可知, $ \angle BMN = \angle N = 90^{\circ} $, 由折叠可知, $ \angle MBC = \angle N = 90^{\circ} $, $ MN = MB $, $ \therefore \angle BMN = \angle N = \angle MBC = 90^{\circ} $. $ \therefore $ 四边形 $ MNCB $ 是矩形. 又 $ \because MN = MB $, $ \therefore $ 矩形 $ MNCB $ 是正方形.
(2) $ \because MN = 4 $, $ \therefore NC = BC = MN = 4 $. $ \therefore AC = \frac{1}{2}NC = 2 $. 在 $ Rt \triangle ABC $ 中, $ AB = \sqrt{AC^{2} + BC^{2}} = \sqrt{2^{2} + 4^{2}} = 2\sqrt{5} $. 由折叠可知, $ AD = AB = 2\sqrt{5} $, $ \therefore BE = CD = AD - AC = 2\sqrt{5} - 2 $. $ \therefore \frac{BE}{BC} = \frac{2\sqrt{5} - 2}{4} = \frac{\sqrt{5} - 1}{2} $. $ \therefore $ 矩形 $ BCDE $ 是黄金矩形.
(1) 证明: 由矩形的性质可知, $ \angle BMN = \angle N = 90^{\circ} $, 由折叠可知, $ \angle MBC = \angle N = 90^{\circ} $, $ MN = MB $, $ \therefore \angle BMN = \angle N = \angle MBC = 90^{\circ} $. $ \therefore $ 四边形 $ MNCB $ 是矩形. 又 $ \because MN = MB $, $ \therefore $ 矩形 $ MNCB $ 是正方形.
(2) $ \because MN = 4 $, $ \therefore NC = BC = MN = 4 $. $ \therefore AC = \frac{1}{2}NC = 2 $. 在 $ Rt \triangle ABC $ 中, $ AB = \sqrt{AC^{2} + BC^{2}} = \sqrt{2^{2} + 4^{2}} = 2\sqrt{5} $. 由折叠可知, $ AD = AB = 2\sqrt{5} $, $ \therefore BE = CD = AD - AC = 2\sqrt{5} - 2 $. $ \therefore \frac{BE}{BC} = \frac{2\sqrt{5} - 2}{4} = \frac{\sqrt{5} - 1}{2} $. $ \therefore $ 矩形 $ BCDE $ 是黄金矩形.
查看更多完整答案,请扫码查看


