《2025年名校课堂九年级数学上册北师大版》

6. 如图,在$\triangle ABC$中,点D,E分别在边AC,AB上,BD,CE相交于点O,且$\frac {EO}{BO}= \frac {DO}{CO}$。求证：$\triangle ADE\backsim \triangle ABC$。
证明：$\because \frac {EO}{BO}=\frac {DO}{CO},\therefore \frac {EO}{DO}=\frac {BO}{CO}.\because ∠BOE=∠COD,\therefore △BOE$$\backsim △COD$.$\therefore ∠EBO=∠DCO.\because ∠A=∠A,\therefore △ABD$$\backsim △ACE$.$\therefore \frac {AD}{AE}=\frac {AB}{AC}.\therefore \frac {AD}{AB}=\frac {AE}{AC}$.又$\because ∠A=∠A,\therefore △ADE\backsim △ABC.$

答案： 证明：$\because \frac {EO}{BO}=\frac {DO}{CO},\therefore \frac {EO}{DO}=\frac {BO}{CO}.\because ∠BOE=∠COD,\therefore △BOE$
$\backsim △COD.\therefore ∠EBO=∠DCO.\because ∠A=∠A,\therefore △ABD\backsim$
$△ACE.\therefore \frac {AD}{AE}=\frac {AB}{AC}.\therefore \frac {AD}{AB}=\frac {AE}{AC}$.又$\because ∠A=∠A,\therefore △ADE\backsim$
$△ABC.$

7. (2023·大庆)在综合与实践课上,老师组织同学们以“矩形的折叠”为主题开展数学活动。有一张矩形纸片ABCD如图所示,点N在边AD上,现将矩形折叠,折痕为BN,点A对应的点记为点M。若点M恰好落在边DC上,则图中与$\triangle NDM$一定相似的三角形是$△MCB$。

答案： $△MCB$

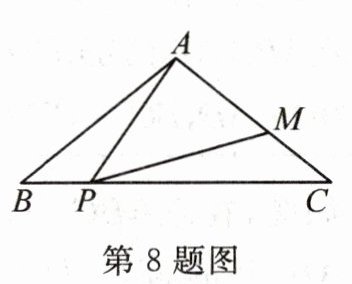
8. 如图,在$\triangle ABC$中,$AB= AC= 5,BC= 8$,P为边BC上一动点(不与点B,C重合),过点P作射线PM交AC于点M,使$∠APM= ∠B$。当$BP= 2$时,CM的长为$\frac {12}{5}$。

答案： $\frac {12}{5}$

9. 如图,$\triangle ABC$为等边三角形,点D在线段CB的延长线上,点E在线段AC的延长线上,连接AD,DE,$∠ADE= ∠ABC$。
(1)求证：$\triangle ADB\backsim \triangle DEC$。
(2)若$BC= 4,DB= 2$,求EC的长。
(1) 证明：$\because △ABC$为等边三角形，$\therefore ∠ABC=∠ACB=$60°.$\therefore ∠ABD=∠DCE=180^{\circ }-$60°$=120^{\circ }.\because ∠ADB+∠CDE=∠ADE=∠ABC=$60°,$∠CDE+∠E=∠ACB=$60°,$\therefore ∠ADB=∠E.\therefore △ADB\backsim △DEC$.
(2)$\because BC=4,DB=2,\therefore DC=BC+DB=$6.$\because △ABC$为等边三角形，$\therefore AB=BC=$4. 由(1)知，$△ADB\backsim △DEC,\therefore \frac {DB}{EC}=\frac {AB}{DC}$，即$\frac {2}{EC}=\frac {4}{6}.\therefore EC=$3.

答案： 解：
(1) 证明：$\because △ABC$为等边三角形，$\therefore ∠ABC=∠ACB=$
$60^{\circ }.\therefore ∠ABD=∠DCE=180^{\circ }-60^{\circ }=120^{\circ }.\because ∠ADB+∠CDE$
$=∠ADE=∠ABC=60^{\circ },∠CDE+∠E=∠ACB=60^{\circ },\therefore$
$∠ADB=∠E.\therefore △ADB\backsim △DEC$.
(2)$\because BC=4,DB=2,\therefore DC$
$=BC+DB=6.\because △ABC$为等边三角形，$\therefore AB=BC=4$. 由
(1)
知，$△ADB\backsim △DEC,\therefore \frac {DB}{EC}=\frac {AB}{DC}$，即$\frac {2}{EC}=\frac {4}{6}.\therefore EC=3.$