《2025年名校课堂九年级数学上册北师大版》

9.(2024·宁夏)为考查一种枸杞幼苗的成活率,在同一条件下进行移植试验,结果如表所示:

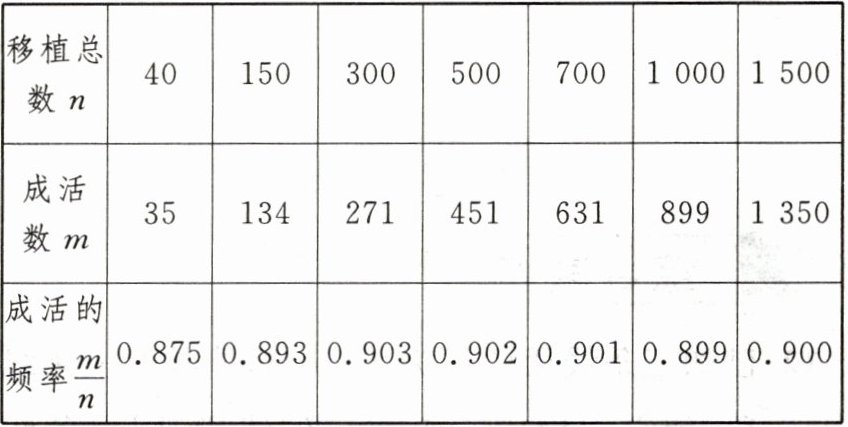
估计这种幼苗移植成活的概率是0.9(结果精确到0.1).

答案： 0.9

10.某同学现有一个只装有若干个黄球的袋子.为了估计袋子中黄球的数量,该同学向这袋黄球中放入了30个绿球(所有球除颜色外其余均相同),摇匀后随机抓取60个,其中绿球共计10个,则袋子中黄球的数量约为 (D)
A.200个
B.180个
C.240个
D.150个

答案： D

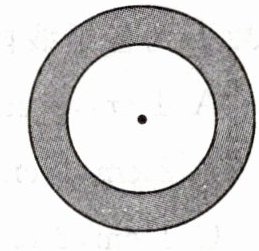
11.小红和小明在操场做游戏,他们先在地上画了半径分别2m和3m的同心圆(如图),然后两个人蒙上眼,在一定距离外向圈内掷小石子,掷中阴影部分小红胜,否则小明胜,未掷入圈内或掷中两圆的边界线则重掷.
(1)如果你来当裁判,你认为游戏公平吗?为什么?
(2)游戏结束,小明边走边想:“反过来,能否用频率估计概率的方法,来估算某一不规则图形的面积呢?”请设计方案,解决这一问题.(要求补充完整图形,说明设计步骤、原理,写出估算公式)

答案：
解:
(1) 不公平. 理由如下: $\because P$ (掷中阴影) $=\frac{9 \pi - 4 \pi}{9 \pi}=\frac{5}{9}$, 即小红获胜的概率为 $\frac{5}{9}$, $\therefore$ 小明获胜的概率为 $1 - \frac{5}{9}=\frac{4}{9}$. $\because \frac{5}{9} ＞ \frac{4}{9}$, $\therefore$ 游戏对双方不公平.
(2) 能利用频率估计概率的试验方法估算非规则图形的面积. 设计方案: ①设计一个可测量面积的规则图形, 将不规则图形围起来 (如正方形, 其面积为 $S$ ), 如图所示.
②往图形中掷点 (如蒙上眼, 往图形中随意掷石子, 掷在图形边界和图外不作记录).
③当掷点次数充分大 (如 1 万次), 记录并统计结果, 设掷入正方形内 $m$ 次, 其中 $n$ 次掷入不规则图形内.
④设不规则图形的面积为 $S_{1}$, 用频率估计概率, 即频率 $P^{\prime}$ (掷入不规则图形内) $=\frac{n}{m} \approx$ 概率 $P$ (掷入不规则图形内) $=\frac{S_{1}}{S}$, 故 $\frac{n}{m} \approx \frac{S_{1}}{S} . \therefore S_{1} \approx \frac{n S}{m}$.