《2025年名校课堂九年级数学上册北师大版》

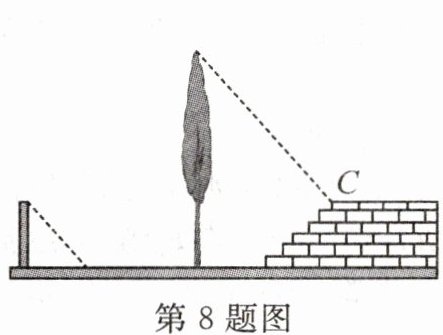
8. 数学兴趣小组的同学们想利用树影测量树高. 课外活动时他们在阳光下测得一根长为1米的竹竿的影子是0.9米,同一时刻测量树高时,发现树的影子不全落在地面上,有一部分影子落在教学楼的台阶上,且影子的末端刚好落在最后一级台阶的上端C处. 他们测得落在地面的影长为1.1米,台阶总的高度为1米,台阶水平总宽度为1.6米,则树高为 (B)

A. 3米
B. 4米
C. 5米
D. 6米

答案： B

9. 如图,在某小区内拐角处的一段道路上,有一儿童在点C处玩耍,一辆汽车从被楼房遮挡的拐角另一侧的A处驶来(CM⊥DM,BD⊥DM,BC与DM相交于点O),已知OM= 4米,CO= 5米,DO= 3米,AO= √{73}米,则汽车从点A处前行的距离AB= 5.75米时,才能发现点C处的儿童.

答案： 5.75

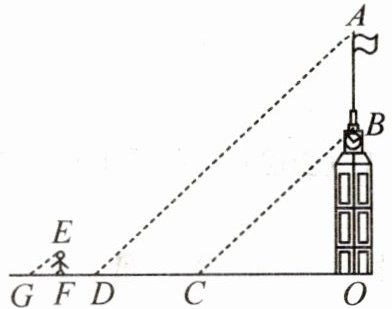
10. 小玉和小武学习完第四章“图形的相似”以后,根据所学知识利用阳光下的影子去测量学校附近一幢建筑物顶部旗杆的高. 如图所示,在某一时刻,他们在阳光下,分别测得该建筑物OB的影长OC为30米,OA的影长OD为50米. 若此时小武的影长FG为2.4米,其中O,C,D,F,G五点在同一条直线上,A,B,O三点在同一条直线上,且AO⊥OD,EF⊥FG. 已知小武的身高EF为1.8米,求旗杆的高AB.

解：由题意可得，$ AD // EG $，$\therefore \angle ADO = \angle EGF $。$\because \angle AOD = \angle EFG = 90^\circ $，$\therefore \triangle AOD \backsim \triangle EFG $。$\therefore \frac{AO}{EF} = \frac{OD}{FG} $，即 $\frac{AO}{1.8} = \frac{50}{2.4} $。$\therefore AO = $37.5。同理可得 $\triangle BOC \backsim \triangle AOD $，$\therefore \frac{BO}{AO} = \frac{OC}{OD} $，即 $\frac{BO}{37.5} = \frac{30}{50} $。$\therefore BO = $22.5。$\therefore AB = AO - BO = 37.5 - 22.5 = $15（米）。答：旗杆的高 $ AB $ 是 15 米。

答案： 解：由题意可得，$ AD // EG $，$\therefore \angle ADO = \angle EGF $。$\because \angle AOD = \angle EFG = 90^\circ $，$\therefore \triangle AOD \backsim \triangle EFG $。$\therefore \frac{AO}{EF} = \frac{OD}{FG} $，即 $\frac{AO}{1.8} = \frac{50}{2.4} $。$\therefore AO = 37.5 $。同理可得 $\triangle BOC \backsim \triangle AOD $，$\therefore \frac{BO}{AO} = \frac{OC}{OD} $，即 $\frac{BO}{37.5} = \frac{30}{50} $。$\therefore BO = 22.5 $。$\therefore AB = AO - BO = 37.5 - 22.5 = 15 $（米）。答：旗杆的高 $ AB $ 是 15 米。

11. 某校社会实践小组为了测量某古建筑的高度,如图,在地面上点C处垂直于地面竖立了高度为2米的标杆CD,此时地面上的点E,标杆的顶端D,该古建筑的塔尖B正好在同一条直线上,测得EC= 4米. 将标杆CD向后平移到点G处,此时地面上的点F,标杆的顶端H,该古建筑的塔尖B正好在同一条直线上(点F,G,E,C与塔底处的点A在同一条直线上),这时测得FG= 6米,GC= 53米,请你根据以上数据,求出该古建筑的高度AB为55米。

答案： 解：由题意，得 $ HG \perp FG $，$DC \perp EC$，$BA \perp FA $，$\therefore \angle HGF = \angle DCE = \angle BAF = 90^\circ $，$ HG // DC // BA $。$\therefore \triangle EDC \backsim \triangle EBA $，$\triangle FHG \backsim \triangle FBA $。$\therefore \frac{HG}{BA} = \frac{FG}{FA} $，$\frac{DC}{BA} = \frac{EC}{EA} $。$\because DC = HG $，$\therefore \frac{FG}{FA} = \frac{EC}{EA} $。$\therefore \frac{6}{53 + 6 + CA} = \frac{4}{4 + CA} $。$\therefore CA = 106 $。$\because \frac{DC}{BA} = \frac{EC}{EA} $，$\therefore \frac{2}{BA} = \frac{4}{4 + 106} $。$\therefore AB = 55 $。答：该古建筑的高度 $ AB $ 为 55 米。