第86页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
1. 如图,已知$\triangle ABC \backsim \triangle DEF$,$AB:DE = 1:2$,则下列等式一定成立的是(

A. $\frac{BC}{DF} = \frac{1}{2}$
B. $\frac{\angle A的度数}{\angle D的度数} = \frac{1}{2}$
C. $\frac{\triangle ABC的面积}{\triangle DEF的面积} = \frac{1}{2}$
D. $\frac{\triangle ABC的周长}{\triangle DEF的周长} = \frac{1}{2}$
D
)
A. $\frac{BC}{DF} = \frac{1}{2}$
B. $\frac{\angle A的度数}{\angle D的度数} = \frac{1}{2}$
C. $\frac{\triangle ABC的面积}{\triangle DEF的面积} = \frac{1}{2}$
D. $\frac{\triangle ABC的周长}{\triangle DEF的周长} = \frac{1}{2}$
答案:
D
2. 如图,顽皮的小聪在小芳的作业本上画了一个“×”(作业本中的横格线都平行,且相邻两条横格线间的距离都相等),点$A$,$B$,$C$,$D$,$O$都在横格线上,且线段$AD$,$BC交于点O$。若线段$AB = 4cm$,则线段$CD$的长为(
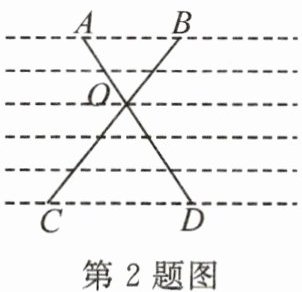
A. $4cm$
B. $5cm$
C. $6cm$
D. $8cm$
C
)
A. $4cm$
B. $5cm$
C. $6cm$
D. $8cm$
答案:
C
3. 如图,在$\triangle ABC$中,$CD平分\angle ACB$,交$AB于点D$,过点$D作BC的平行线交AC于点M$。若$BC = 3$,$AC = 2$,则$DM$的长为(
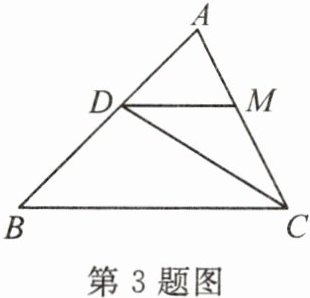
A. $\frac{5}{6}$
B. $\frac{6}{5}$
C. $\frac{3}{4}$
D. $\frac{4}{3}$
B
)
A. $\frac{5}{6}$
B. $\frac{6}{5}$
C. $\frac{3}{4}$
D. $\frac{4}{3}$
答案:
B
4. 西周数学家商高总结了用“矩”(如图1)测量物高的方法:把矩的两边按图2放置,从“矩”$CDA的一端A$(人眼)望点$E$,使视线通过“矩”的另一端点$C$,记人站立的位置为点$B$,量出$BG$的长,即可算得物高$EG$。若$a = 30cm$,$b = 60cm$,$AB = 1.6m$,$BG = 2.4m$,则$EG$的高度为(
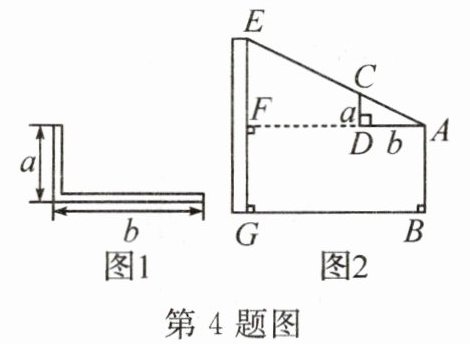
A. $1.2m$
B. $2.8m$
C. $4.8m$
D. $6.4m$
B
)
A. $1.2m$
B. $2.8m$
C. $4.8m$
D. $6.4m$
答案:
B
5. 如图,将腰长为$12cm$的等腰三角形纸片,沿与底边平行的方向剪去一个小的等腰三角形纸片,剩下一个等腰梯形纸片。若剪去纸片面积是剩下的纸片面积的$\frac{1}{8}$,则剪去等腰三角形纸片的腰长为
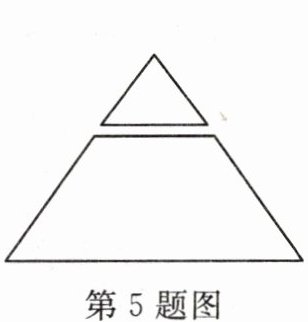
4
$cm$。
答案:
4
6. 如图,$E是□ ABCD的边AD$上的一点,且$\frac{DE}{AE} = \frac{1}{2}$,连接$BE并延长交CD的延长线于点F$。若$DE = 3$,$DF = 4$,则$□ ABCD$的周长为
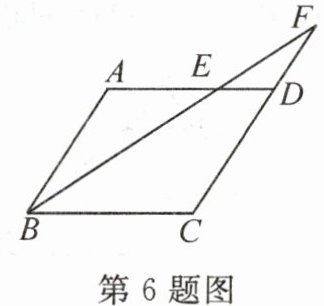
34
。
答案:
34
7. 如图,在$\triangle ABC$中,$AB < AC$,将$\triangle ABC绕点A逆时针旋转得到\triangle ADE$,点$D在边BC$上,$DE交AC于点F$。若$AC = 8$,$BD = 2$,$BC = 6$,则$\frac{DF}{AF} = $
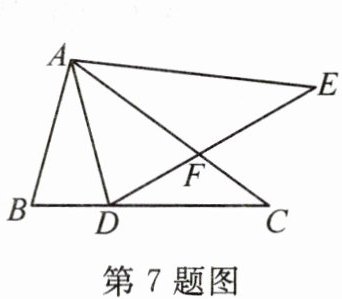
$\frac{1}{2}$
。
答案:
$\frac{1}{2}$
8. 新考向 真实情境 有五本形状为长方体的书放置在方形书架中,如图所示,其中四本竖放,第五本斜放,点$G$正好在书架边框上。若每本书的厚度为$5cm$,高度为$20cm$,书架宽为$40cm$,则$FI$的长为
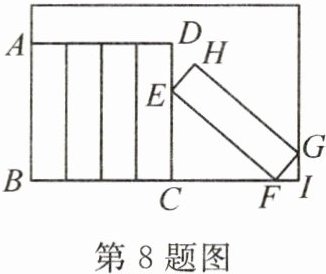
$\frac{40}{17}$
$cm$。
答案:
$\frac{40}{17}$
查看更多完整答案,请扫码查看


