第34页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
1. 如图,从一块正方形木板上锯掉2m宽的矩形木板后,剩下的矩形木板的面积是$24m^2,$则原来这块木板的边长是(
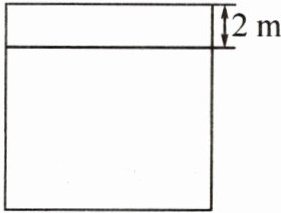
A. 2m
B. 4m
C. 6m
D. 36m
C
)
A. 2m
B. 4m
C. 6m
D. 36m
答案:
C
2. (2024·青岛)如图,某小区要在长为16m,宽为12m的矩形空地上建造一个花坛,使花坛四周小路的宽度相等,且花坛所占面积为矩形空地面积的一半,则小路的宽为
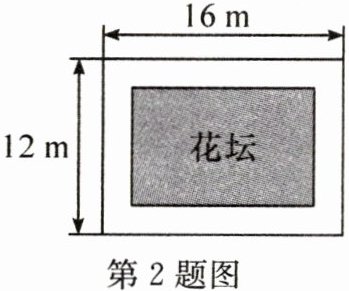
2
m.
答案:
2
3. (教材P38习题T2变式)如图,在宽为4m,长为6m的矩形绿地上铺设两条同样宽的小路(两条小路各与矩形的一条边平行),余下部分种植小草. 若种植小草的面积为$15m^2,$则铺设的小路的宽应为
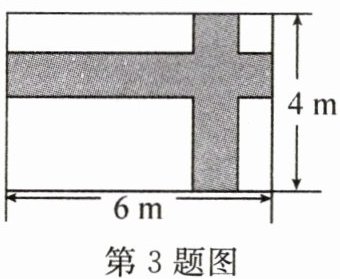
1
m.
答案:
1
4. (2023·淮安改编)为了便于劳动课程的开展,学校打算建一个矩形生态园ABCD(如图),生态园一面靠墙,另外三面用18m的篱笆围成.
(1)生态园的面积能否为$40m^2?$如果能,请求出AB的长;如果不能,请说明理由.
(2)生态园的面积____为$50m^2.($填“能”或“不能”)

(1)生态园的面积能否为$40m^2?$如果能,请求出AB的长;如果不能,请说明理由.
(2)生态园的面积____为$50m^2.($填“能”或“不能”)

解:生态园的面积能为 $40m^{2}$。理由如下:∵四边形 $ABCD$ 是矩形,∴ $AB = CD$, $AD = BC$。设 $AB = xm$,则 $BC=\frac{18 - x}{2}m$。由题意,得 $x\cdot\frac{18 - x}{2}=40$,解得 $x_{1}=10$, $x_{2}=8$。∴生态园的面积能为 $40m^{2}$, $AB$ 的长为 $10m$ 或 $8m$。
不能
答案:
解:生态园的面积能为 $40m^{2}$。理由如下:
∵四边形 $ABCD$ 是矩形,
∴ $AB = CD$, $AD = BC$。设 $AB = xm$,则 $BC=\frac{18 - x}{2}m$。由题意,得 $x\cdot\frac{18 - x}{2}=40$,解得 $x_{1}=10$, $x_{2}=8$。
∴生态园的面积能为 $40m^{2}$, $AB$ 的长为 $10m$ 或 $8m$。
(2)不能
∵四边形 $ABCD$ 是矩形,
∴ $AB = CD$, $AD = BC$。设 $AB = xm$,则 $BC=\frac{18 - x}{2}m$。由题意,得 $x\cdot\frac{18 - x}{2}=40$,解得 $x_{1}=10$, $x_{2}=8$。
∴生态园的面积能为 $40m^{2}$, $AB$ 的长为 $10m$ 或 $8m$。
(2)不能
5. (2024·通辽)如图,小程的爸爸用一段10m长的铁丝网围成一个一边靠墙(墙长5.5m)的矩形鸭舍,其面积为$15m^2,$在鸭舍侧面中间位置留一个1m宽的门(由其他材料制成),则BC的长为(

A. 5m或6m
B. 2.5m或3m
C. 5m
D. 3m
C
)
A. 5m或6m
B. 2.5m或3m
C. 5m
D. 3m
答案:
C
6. 如图,从一张长为40cm,宽为30cm的矩形纸板的四个角上分别剪掉2个小正方形和2个小矩形(阴影部分即剪掉的部分),剩余的部分可以折成一个有盖的长方体盒子(纸板的厚度忽略不计). 若折成的长方体盒子的表面积是$950cm^2,$设小正方形的边长为xcm.
(1)请用含x的代数式表示长方体盒子底面的长和宽.
长方体盒子底面的长为
(2)长方体盒子的体积为多少?
长方体盒子的体积为
(1)请用含x的代数式表示长方体盒子底面的长和宽.
长方体盒子底面的长为
$(30 - 2x)cm$
,宽为$(20 - x)cm$
.(2)长方体盒子的体积为多少?
长方体盒子的体积为
$1500cm^3$
.
答案:
解:
(1)
∵小正方形的边长为 $xcm$,矩形纸板的长和宽分别为 $40cm$ 和 $30cm$,
∴长方体盒子底面的长为 $(30 - 2x)cm$,宽为 $\frac{40 - 2x}{2}=(20 - x)cm$。
(2)依题意,得 $40×30 - 2x^{2}-2×\frac{40}{2}x = 950$。整理,得 $x^{2}+20x - 125 = 0$。解得 $x_{1}=5$, $x_{2}=-25$(不合题意,舍去)。
∴ $30 - 2x = 30 - 2×5 = 20$, $20 - x = 20 - 5 = 15$。
∴长方体盒子的体积为 $20×15×5 = 1500(cm^{3})$。答:长方体盒子的体积为 $1500cm^{3}$。
(1)
∵小正方形的边长为 $xcm$,矩形纸板的长和宽分别为 $40cm$ 和 $30cm$,
∴长方体盒子底面的长为 $(30 - 2x)cm$,宽为 $\frac{40 - 2x}{2}=(20 - x)cm$。
(2)依题意,得 $40×30 - 2x^{2}-2×\frac{40}{2}x = 950$。整理,得 $x^{2}+20x - 125 = 0$。解得 $x_{1}=5$, $x_{2}=-25$(不合题意,舍去)。
∴ $30 - 2x = 30 - 2×5 = 20$, $20 - x = 20 - 5 = 15$。
∴长方体盒子的体积为 $20×15×5 = 1500(cm^{3})$。答:长方体盒子的体积为 $1500cm^{3}$。
7. 如图,在一块长为30m,宽为24m的矩形花圃内修建四条宽度相等,
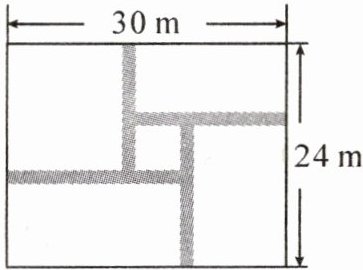
且各与矩形的一条边垂直的小路,四条小路围成的中间部分恰好是一个正方形,且边长是小路宽度的4倍. 若四条小路的总面积为$80m^2,$则小路的宽为

且各与矩形的一条边垂直的小路,四条小路围成的中间部分恰好是一个正方形,且边长是小路宽度的4倍. 若四条小路的总面积为$80m^2,$则小路的宽为
$\frac{5}{4}$
m.
答案:
$\frac{5}{4}$
查看更多完整答案,请扫码查看


