《2025年名校课堂九年级数学上册北师大版》

2. 在学习镜面反射后,小明知道了当入射光线与镜面垂直时,反射光线将与入射光线重合,沿原路返回.他利用此现象设计了一个测量物体高度的工具.

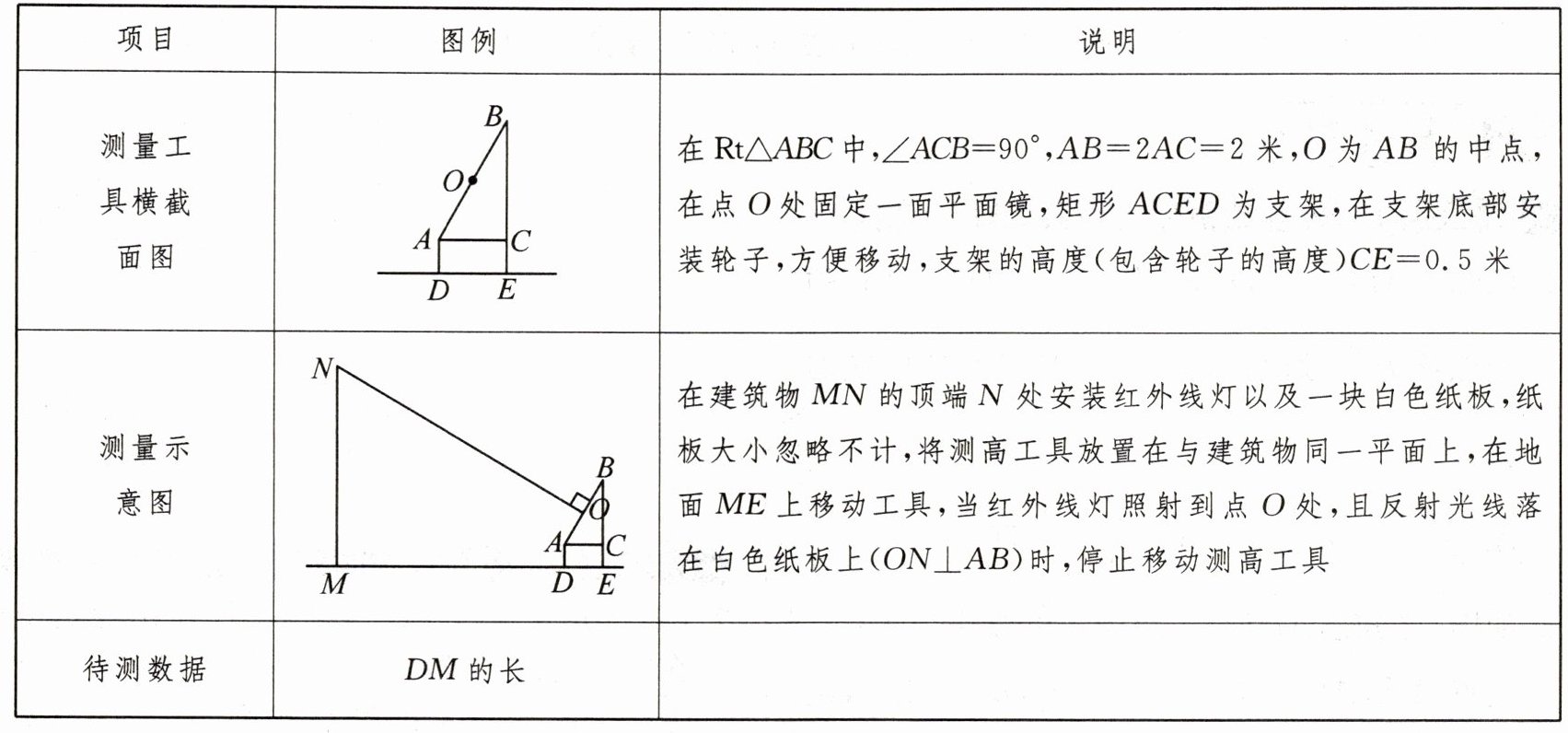
在一次实际测量过程中,小明测得测高工具与建筑物的水平距离DM= 5.5米,请计算建筑物MN的高度(结果精确到0.1米,参考数据:$\sqrt{3}\approx 1.73$).
答：建筑物MN的高度约为4.8米。

答案： 解：过点$O$分别作$OQ\perp MN$于点$Q$，$OP\perp ME$于点$P$，交$AC$于点$H$。$\because OQ\perp MN$，$OP\perp ME$，且$\angle NMD=90^{\circ}$，$\therefore$ 四边形$QMPO$为矩形。$\therefore \angle QOP=90^{\circ}$。$\because NO\perp AB$，$\therefore \angle NOA=90^{\circ}$。$\therefore \angle NOQ=\angle AOH$。$\because \angle NQO=\angle AHO=90^{\circ}$，$\therefore \triangle NQO\backsim \triangle AHO$。$\therefore \frac{NQ}{QO}=\frac{AH}{HO}$。$\because AB=2AC=2$ 米，$\therefore \angle B=30^{\circ}$。$\because OH\perp AC$，$BC\perp AC$，$\therefore OH// BC$。$\because$ 点$O$为$AB$的中点，$\therefore AH=\frac{1}{2}AC=0.5$ 米，$AO=\frac{1}{2}AB=1$ 米。$\therefore DP=AH=0.5$ 米，$OH=\sqrt{AO^{2}-AH^{2}}=\frac{\sqrt{3}}{2}$ 米。$\therefore QO=MP=MD+DP=5.5+0.5=6$ (米)。$\therefore \frac{NQ}{6}=\frac{0.5}{\frac{\sqrt{3}}{2}}$，解得$NQ=2\sqrt{3}$。$\because QM=OP=OH+HP=(\frac{\sqrt{3}}{2}+0.5)$ 米，$\therefore MN=NQ+QM=2\sqrt{3}+\frac{\sqrt{3}}{2}+0.5=\frac{5\sqrt{3}}{2}+\frac{1}{2}\approx 4.8$ (米)。答：建筑物$MN$的高度约为 4.8 米。