《2025年名校课堂九年级数学上册北师大版》

10. 新考向 真实情境 图1是装了液体的高脚杯示意图(数据如图),用去一部分液体后如图2所示,此时液面$AB= $ (C)

A. $1cm$
B. $2cm$
C. $3cm$
D. $4cm$

答案： C

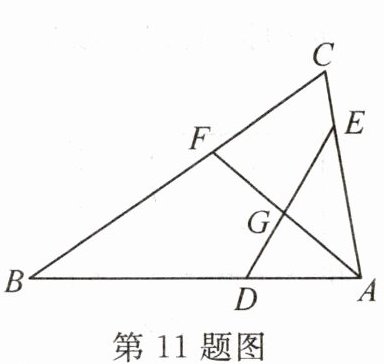
11. 如图,在$\triangle ABC$中,点$D$,$E分别在AB$,$AC$上,$AF平分\angle BAC交DE于点G$。若$AE= 3$,$EC= 1$,$AD= 2$,$BD= 4$,则$AG:AF$的值为$\frac{1}{2}$。

答案： $\frac{1}{2}$

12. 如图,已知$\triangle ABC \backsim \triangle A'B'C'$,它们的相似比为$k$,$AD$,$A'D'$是对应的中线。求证：$\frac{AD}{A'D'}= \frac{AB}{A'B'}= k$。

答案： 证明: $\because \triangle ABC\backsim\triangle A'B'C'$, $\therefore \frac{AB}{A'B'} = \frac{BC}{B'C'} = k$, $\angle B = \angle B'$. $\because AD$, $A'D'$分别是$\triangle ABC$, $\triangle A'B'C'$的中线, $\therefore BD = \frac{1}{2}BC$, $B'D' = \frac{1}{2}B'C'$. $\therefore \frac{BD}{B'D'} = \frac{\frac{1}{2}BC}{\frac{1}{2}B'C'} = \frac{BC}{B'C'} = \frac{AB}{A'B'} = k$. $\therefore \triangle ABD\backsim\triangle A'B'D'$. $\therefore \frac{AD}{A'D'} = \frac{AB}{A'B'} = k$.

13. 新考向 真实情境 近年来,我国近视发生率呈明显上升趋势,近视已成为影响我国国民尤其是青少年眼健康的重大公共卫生问题。为了加强视力保护意识,小北想在书房里挂一张测试距离为$5m$的视力表,但两面墙的距离只有$3m$。在一次课题学习综合实践课上,小北向全班同学征集“解决空间过小,如何放置视力表问题”的方案,其中甲、乙两位同学设计方案新颖,构思巧妙。

(1) 在甲同学的方案中,如果大视力表中“E”的高为$0.035m$,那么小视力表中相应“E”的高是0.021米？
(2) 在乙同学的方案中,如果视力表的全长($AB$)为$1.6m$,那么$MN$至少为0.64米？

答案： 解:
(1) 由题意可得, $BC\perp AB$, $DF\perp AD$, $\therefore \angle CBA = \angle FDA = 90^{\circ}$. 又 $\because \angle CAB = \angle FAD$, $\therefore \triangle CAB\backsim\triangle FAD$. $\therefore \frac{AD}{AB} = \frac{DF}{BC}$. $\therefore \frac{3}{5} = \frac{DF}{0.035}$, 解得 $DF = 0.021$. 答: 小视力表中相应“E”的高是 0.021 m.
(2) 作 $CD\perp MN$ 于点 D, 延长 CD 交 $A'B'$ 于点 E. 由题意可得, $AB// MN// A'B'$. $\because MN// A'B'$, $CD\perp MN$, $\therefore CE\perp A'B'$. $\because MN// A'B'$, $\therefore \angle MNC = \angle A'B'C$, $\angle NMC = \angle B'A'C$. $\therefore \triangle MNC\backsim\triangle A'B'C$. $\therefore \frac{MN}{A'B'} = \frac{CD}{CE}$. 由题意可得, $CE = 5m$, $DE = 3m$, $A'B' = AB = 1.6m$, $\therefore CD = CE - DE = 2m$. $\therefore \frac{MN}{1.6} = \frac{2}{5}$. $\therefore MN = 0.64m$. 答: $MN$ 至少为 0.64 m.