第23页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
1. 关于菱形的性质,以下说法不正确的是(
A. 四条边相等
B. 对角线相等
C. 对角线互相垂直
D. 是轴对称图形
B
)A. 四条边相等
B. 对角线相等
C. 对角线互相垂直
D. 是轴对称图形
答案:
B
2. 新考向 开放性问题
如图,将$\triangle ABC$沿BC方向平移得到$\triangle DEF$,只需添加一个条件即可证明四边形ABED是菱形,这个条件可以是

如图,将$\triangle ABC$沿BC方向平移得到$\triangle DEF$,只需添加一个条件即可证明四边形ABED是菱形,这个条件可以是
$ AB = AD $
.(写出一个即可)
答案:
$ AB = AD $ (答案不唯一)
3. 新考向 传统文化 “福”字象征着中华民族的历史文化与精神.图1是小红家大门上的“福”字,图2是抽离出来的菱形ABCD,对角线AC,BD相交于点O,$∠ABC= 80^{\circ }$,E是线段AO上一点,且$BC= CE$,则$∠OBE$的度数是______
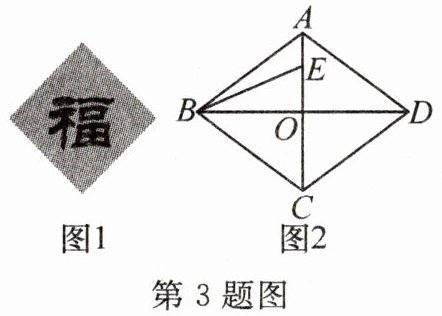
25°
.
答案:
$ 25^{\circ} $
4. (2024·青岛)如图,在菱形ABCD中,$BC= 10$,其面积为60,对角线AC与BD相交于点O,过点A作$AE⊥BC$,交边BC于点E,连接EO,则$EO=$
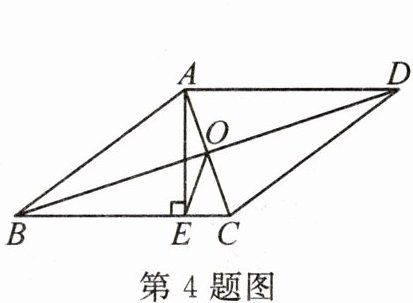
$\sqrt{10}$
.
答案:
$ \sqrt{10} $
5. 依据所标数据,下列四边形不一定为矩形的是(
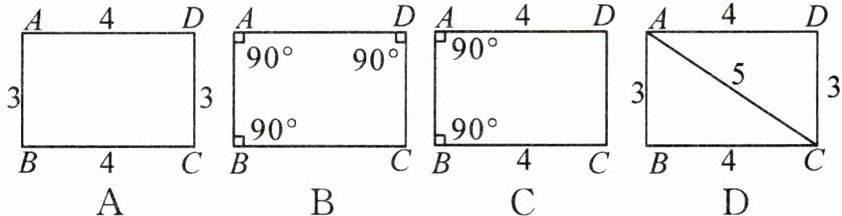
A
)
答案:
A
6. (2024·东营)如图,四边形ABCD是矩形,直线EF分别交AD,BC,BD于点E,F,O,下列条件中,不能证明$\triangle BOF\cong \triangle DOE$的是(
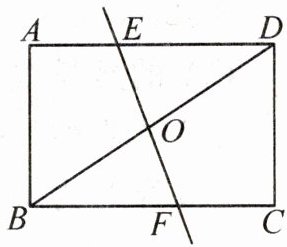
A. O为矩形ABCD两条对角线的交点
B. $EO= FO$
C. $AE= CF$
D. $EF⊥BD$
D
)
A. O为矩形ABCD两条对角线的交点
B. $EO= FO$
C. $AE= CF$
D. $EF⊥BD$
答案:
D
7. (2023·河南)在矩形ABCD中,M为对角线BD的中点,点N在边AD上,且$AN= AB= 1$.当以点D,M,N为顶点的三角形是直角三角形时,AD的长为
2 或 $ 1 + \sqrt{2} $
.
答案:
2 或 $ 1 + \sqrt{2} $
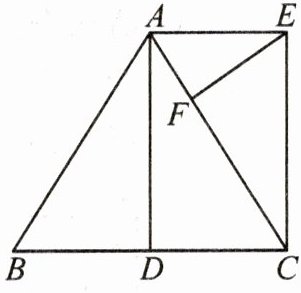
8. (2024·兰州)如图,在$\triangle ABC$中,$AB= AC$,D是BC的中点,$CE// AD,AE⊥AD,EF⊥AC$.
(1)求证:四边形ADCE是矩形.
(2)若$BC= 4,CE= 3$,求EF的长.
(1) 证明: $ \because $ 在 $ \triangle ABC $ 中, $ AB = AC $, $ D $ 是 $ BC $ 的中点, $ \therefore AD \perp BC $, 即 $ \angle ADC = \angle ADB = 90^{\circ} $. $ \because CE // AD $, $ \therefore \angle ECD = \angle ADB = 90^{\circ} $. $ \because AE \perp AD $, $ \therefore \angle EAD = 90^{\circ} $. $ \therefore \angle ADC = \angle ECD = \angle EAD = 90^{\circ} $. $ \therefore $ 四边形 $ ADCE $ 是矩形. (2) $ \because $ 在 $ \triangle ABC $ 中, $ AB = AC $, $ D $ 是 $ BC $ 的中点, $ BC = 4 $, $ \therefore BD = CD = \frac{1}{2}BC = 2 $. 由 (1) 可知, 四边形 $ ADCE $ 是矩形, $ \therefore AE = CD = 2 $, $ \angle AEC = 90^{\circ} $, 在 $ Rt \triangle AEC $ 中, $ AE = 2 $, $ CE = 3 $, 由勾股定理, 得 $ AC = \sqrt{AE^{2} + CE^{2}} = \sqrt{13} $, $ \because EF \perp AC $, 由三角形的面积公式, 得 $ S_{\triangle AEC} = \frac{1}{2}AC \cdot EF = \frac{1}{2}AE \cdot CE $, $ \therefore EF = \frac{AE \cdot CE}{AC} = \frac{2 × 3}{\sqrt{13}} = $
(1)求证:四边形ADCE是矩形.
(2)若$BC= 4,CE= 3$,求EF的长.

(1) 证明: $ \because $ 在 $ \triangle ABC $ 中, $ AB = AC $, $ D $ 是 $ BC $ 的中点, $ \therefore AD \perp BC $, 即 $ \angle ADC = \angle ADB = 90^{\circ} $. $ \because CE // AD $, $ \therefore \angle ECD = \angle ADB = 90^{\circ} $. $ \because AE \perp AD $, $ \therefore \angle EAD = 90^{\circ} $. $ \therefore \angle ADC = \angle ECD = \angle EAD = 90^{\circ} $. $ \therefore $ 四边形 $ ADCE $ 是矩形. (2) $ \because $ 在 $ \triangle ABC $ 中, $ AB = AC $, $ D $ 是 $ BC $ 的中点, $ BC = 4 $, $ \therefore BD = CD = \frac{1}{2}BC = 2 $. 由 (1) 可知, 四边形 $ ADCE $ 是矩形, $ \therefore AE = CD = 2 $, $ \angle AEC = 90^{\circ} $, 在 $ Rt \triangle AEC $ 中, $ AE = 2 $, $ CE = 3 $, 由勾股定理, 得 $ AC = \sqrt{AE^{2} + CE^{2}} = \sqrt{13} $, $ \because EF \perp AC $, 由三角形的面积公式, 得 $ S_{\triangle AEC} = \frac{1}{2}AC \cdot EF = \frac{1}{2}AE \cdot CE $, $ \therefore EF = \frac{AE \cdot CE}{AC} = \frac{2 × 3}{\sqrt{13}} = $
$\frac{6\sqrt{13}}{13}$
.
答案:
解:
(1) 证明: $ \because $ 在 $ \triangle ABC $ 中, $ AB = AC $, $ D $ 是 $ BC $ 的中点, $ \therefore AD \perp BC $, 即 $ \angle ADC = \angle ADB = 90^{\circ} $. $ \because CE // AD $, $ \therefore \angle ECD = \angle ADB = 90^{\circ} $. $ \because AE \perp AD $, $ \therefore \angle EAD = 90^{\circ} $. $ \therefore \angle ADC = \angle ECD = \angle EAD = 90^{\circ} $. $ \therefore $ 四边形 $ ADCE $ 是矩形.
(2) $ \because $ 在 $ \triangle ABC $ 中, $ AB = AC $, $ D $ 是 $ BC $ 的中点, $ BC = 4 $, $ \therefore BD = CD = \frac{1}{2}BC = 2 $. 由
(1) 可知, 四边形 $ ADCE $ 是矩形, $ \therefore AE = CD = 2 $, $ \angle AEC = 90^{\circ} $, 在 $ Rt \triangle AEC $ 中, $ AE = 2 $, $ CE = 3 $, 由勾股定理, 得 $ AC = \sqrt{AE^{2} + CE^{2}} = \sqrt{13} $, $ \because EF \perp AC $, 由三角形的面积公式, 得 $ S_{\triangle AEC} = \frac{1}{2}AC \cdot EF = \frac{1}{2}AE \cdot CE $, $ \therefore EF = \frac{AE \cdot CE}{AC} = \frac{2 \times 3}{\sqrt{13}} = \frac{6\sqrt{13}}{13} $.
(1) 证明: $ \because $ 在 $ \triangle ABC $ 中, $ AB = AC $, $ D $ 是 $ BC $ 的中点, $ \therefore AD \perp BC $, 即 $ \angle ADC = \angle ADB = 90^{\circ} $. $ \because CE // AD $, $ \therefore \angle ECD = \angle ADB = 90^{\circ} $. $ \because AE \perp AD $, $ \therefore \angle EAD = 90^{\circ} $. $ \therefore \angle ADC = \angle ECD = \angle EAD = 90^{\circ} $. $ \therefore $ 四边形 $ ADCE $ 是矩形.
(2) $ \because $ 在 $ \triangle ABC $ 中, $ AB = AC $, $ D $ 是 $ BC $ 的中点, $ BC = 4 $, $ \therefore BD = CD = \frac{1}{2}BC = 2 $. 由
(1) 可知, 四边形 $ ADCE $ 是矩形, $ \therefore AE = CD = 2 $, $ \angle AEC = 90^{\circ} $, 在 $ Rt \triangle AEC $ 中, $ AE = 2 $, $ CE = 3 $, 由勾股定理, 得 $ AC = \sqrt{AE^{2} + CE^{2}} = \sqrt{13} $, $ \because EF \perp AC $, 由三角形的面积公式, 得 $ S_{\triangle AEC} = \frac{1}{2}AC \cdot EF = \frac{1}{2}AE \cdot CE $, $ \therefore EF = \frac{AE \cdot CE}{AC} = \frac{2 \times 3}{\sqrt{13}} = \frac{6\sqrt{13}}{13} $.
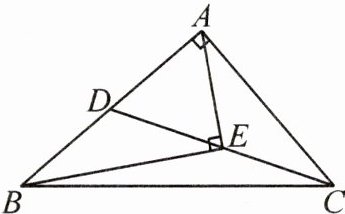
9. 如图,在$Rt\triangle ABC$中,$∠BAC= 90^{\circ },AB= 4$,CD是$\triangle ABC$的中线,E是CD的中点,连接AE,BE.若$AE⊥BE$,垂足为E,则AC的长为
$2\sqrt{3}$
.
答案:
$ 2\sqrt{3} $
查看更多完整答案,请扫码查看


