第77页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
6. 如图,在矩形ABCD中,E是边AD上的任意一点,连接BE,过点E作BE的垂线交BC的延长线于点F,交边CD于点P,则图中共有______对相似三角形(
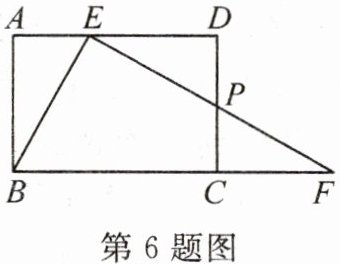
A. 6
B. 5
C. 4
D. 3
A
)
A. 6
B. 5
C. 4
D. 3
答案:
A
7. 如图,四边形ABCD、四边形CDEF和四边形EFGH都是正方形,则△ACF∽
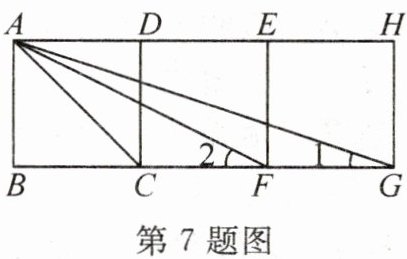
△GCA
,∠1+∠2=45
°.
答案:
$ \triangle GCA $ 45
8. (教材P102习题T3变式)特例感知
(1)如图1,点C,D分别是线段AB的三等分点,以CD为边作等边三角形PCD,连接AP,BP,则∠APB的度数是
类比探究
(2)如图2,在△APB中,∠APB= 120°,点C,D在AB边上,连接PC,PD.若△PCD是等边三角形,请探究线段AC,CD,BD之间的数量关系,并说明理由.
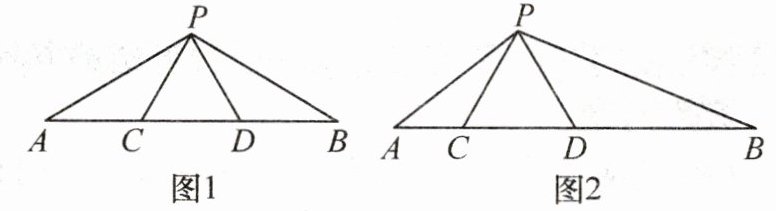
(1)如图1,点C,D分别是线段AB的三等分点,以CD为边作等边三角形PCD,连接AP,BP,则∠APB的度数是
120°
;写出图中一个与∠APC相等的角:∠A
(答案不唯一).类比探究
(2)如图2,在△APB中,∠APB= 120°,点C,D在AB边上,连接PC,PD.若△PCD是等边三角形,请探究线段AC,CD,BD之间的数量关系,并说明理由.

解:(2) $ CD^{2} = AC \cdot BD $。理由:$\because \triangle PCD$ 是等边三角形,$\therefore \angle PCD = \angle PDC = 60^{\circ}$,$PC = PD$。$\therefore \angle DPB + \angle B = 60^{\circ}$,$\angle ACP = \angle PDB = 120^{\circ}$。$\because \angle APB = 120^{\circ}$,$\therefore \angle A + \angle B = 60^{\circ}$。$\therefore \angle A = \angle DPB$。$\therefore \triangle ACP \backsim \triangle PDB$。$\therefore \frac{AC}{DB} = \frac{CP}{PD}$。$\because PC = PD = CD$,$\therefore CD^{2} = AC \cdot BD$。
答案:
解:
(1) $ 120^{\circ} $ $ \angle A $(答案不唯一)
(2) $ CD^{2} = AC \cdot BD $。理由:$\because \triangle PCD$ 是等边三角形,$\therefore \angle PCD = \angle PDC = 60^{\circ}$,$PC = PD$。$\therefore \angle DPB + \angle B = 60^{\circ}$,$\angle ACP = \angle PDB = 120^{\circ}$。$\because \angle APB = 120^{\circ}$,$\therefore \angle A + \angle B = 60^{\circ}$。$\therefore \angle A = \angle DPB$。$\therefore \triangle ACP \backsim \triangle PDB$。$\therefore \frac{AC}{DB} = \frac{CP}{PD}$。$\because PC = PD = CD$,$\therefore CD^{2} = AC \cdot BD$。
(1) $ 120^{\circ} $ $ \angle A $(答案不唯一)
(2) $ CD^{2} = AC \cdot BD $。理由:$\because \triangle PCD$ 是等边三角形,$\therefore \angle PCD = \angle PDC = 60^{\circ}$,$PC = PD$。$\therefore \angle DPB + \angle B = 60^{\circ}$,$\angle ACP = \angle PDB = 120^{\circ}$。$\because \angle APB = 120^{\circ}$,$\therefore \angle A + \angle B = 60^{\circ}$。$\therefore \angle A = \angle DPB$。$\therefore \triangle ACP \backsim \triangle PDB$。$\therefore \frac{AC}{DB} = \frac{CP}{PD}$。$\because PC = PD = CD$,$\therefore CD^{2} = AC \cdot BD$。
9. (教材P102习题T4变式)如图,已知直线l的函数表达式为y= -4/3x+8,且l与x轴、y轴分别交于A,B两点,动点Q从点B开始在线段BA上以每秒2个单位长度的速度向点A移动,同时动点P从点A开始在线段AO上以每秒1个单位长度的速度向点O移动,设点P,Q移动的时间为t秒.
(1)求A,B两点的坐标.
(2)当t为何值时,以A,P,Q为顶点的三角形与△AOB相似?
(3)当△APQ的面积是△ABO面积的1/5时,t的值为______
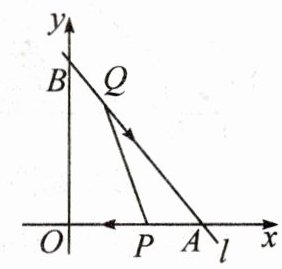
(1)求A,B两点的坐标.
(2)当t为何值时,以A,P,Q为顶点的三角形与△AOB相似?
(3)当△APQ的面积是△ABO面积的1/5时,t的值为______
2 或 3
.
答案:
解:
(1) 对于 $ y = -\frac{4}{3}x + 8 $,令 $ y = 0 $,则 $ -\frac{4}{3}x + 8 = 0 $,解得 $ x = 6 $;令 $ x = 0 $,则 $ y = 8 $。$\therefore A$,$B$ 两点的坐标分别为 $ (6, 0) $,$ (0, 8) $。
(2) 在 $ \text{Rt} \triangle AOB $ 中,$ BO = 8 $,$ AO = 6 $,根据勾股定理,得 $ AB = \sqrt{BO^{2} + AO^{2}} = 10 $。由题意可知,$ AP = t $,$ BQ = 2t $,$ AQ = 10 - 2t $。当 $ \triangle APQ \backsim \triangle AOB $ 时,$ \frac{AP}{AO} = \frac{AQ}{AB} $,$\therefore \frac{t}{6} = \frac{10 - 2t}{10}$,解得 $ t = \frac{30}{11} $;当 $ \triangle APQ \backsim \triangle ABO $ 时,$ \frac{AP}{AB} = \frac{AQ}{AO} $,$\therefore \frac{t}{10} = \frac{10 - 2t}{6}$,解得 $ t = \frac{50}{13} $。综上所述,当 $ t = \frac{30}{11} $ 或 $ \frac{50}{13} $ 时,以 $ A $,$ P $,$ Q $ 为顶点的三角形与 $ \triangle AOB $ 相似。
(3) 2 或 3
(1) 对于 $ y = -\frac{4}{3}x + 8 $,令 $ y = 0 $,则 $ -\frac{4}{3}x + 8 = 0 $,解得 $ x = 6 $;令 $ x = 0 $,则 $ y = 8 $。$\therefore A$,$B$ 两点的坐标分别为 $ (6, 0) $,$ (0, 8) $。
(2) 在 $ \text{Rt} \triangle AOB $ 中,$ BO = 8 $,$ AO = 6 $,根据勾股定理,得 $ AB = \sqrt{BO^{2} + AO^{2}} = 10 $。由题意可知,$ AP = t $,$ BQ = 2t $,$ AQ = 10 - 2t $。当 $ \triangle APQ \backsim \triangle AOB $ 时,$ \frac{AP}{AO} = \frac{AQ}{AB} $,$\therefore \frac{t}{6} = \frac{10 - 2t}{10}$,解得 $ t = \frac{30}{11} $;当 $ \triangle APQ \backsim \triangle ABO $ 时,$ \frac{AP}{AB} = \frac{AQ}{AO} $,$\therefore \frac{t}{10} = \frac{10 - 2t}{6}$,解得 $ t = \frac{50}{13} $。综上所述,当 $ t = \frac{30}{11} $ 或 $ \frac{50}{13} $ 时,以 $ A $,$ P $,$ Q $ 为顶点的三角形与 $ \triangle AOB $ 相似。
(3) 2 或 3
查看更多完整答案,请扫码查看


