第92页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
1. 下列长度的各组线段中,是成比例线段的是(
A. $\sqrt {2},3,2,\sqrt {3}$
B. 4,6,5,10
C. $1,2,\sqrt {2},2\sqrt {2}$
D. 2,3,4,1
C
)A. $\sqrt {2},3,2,\sqrt {3}$
B. 4,6,5,10
C. $1,2,\sqrt {2},2\sqrt {2}$
D. 2,3,4,1
答案:
C
2. 已知$\frac {a}{b}= \frac {4}{3}$,则$\frac {b}{b-2a}$的值为
$-\frac{3}{5}$
.
答案:
$-\frac{3}{5}$
3. 如图,这是某位同学用带有刻度的直尺在数轴上作图的方法.若图中的虚线相互平行,则点P表示的数是(
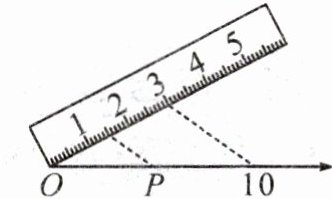
A. 1
B. $\sqrt {2}$
C. $\frac {10}{3}$
D. 5
D
)
A. 1
B. $\sqrt {2}$
C. $\frac {10}{3}$
D. 5
答案:
D
4. (2024·连云港)下列网格中各个小正方形的边长均为1,阴影部分图形分别记作甲、乙、丙、丁,其中是相似形的为(

A. 甲和乙
B. 乙和丁
C. 甲和丙
D. 甲和丁
D
)
A. 甲和乙
B. 乙和丁
C. 甲和丙
D. 甲和丁
答案:
D
5. 符合黄金分割比例形式的图形很容易使人产生视觉上的美感.如图所示的五角星中,$AD= BC$,且C,D两点都是AB的黄金分割点.若$CD= 1$,则AB的长是
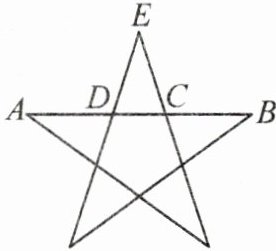
$2+\sqrt{5}$
.(结果保留根号)
答案:
$2+\sqrt{5}$
6. 已知$△ABC\backsim △DEF$,且$AB= 3,DE= 6$.若$△ABC$的周长为20,则$△DEF$的周长为(
A. 5
B. 10
C. 40
D. 80
C
)A. 5
B. 10
C. 40
D. 80
答案:
C
7. 如图,在$△ABC$中,点D,E分别在边AB,AC上,则在下列四个条件中:①$∠AED= ∠B$;②$DE// BC$;③$\frac {AD}{AC}= \frac {AE}{AB}$;④$AD\cdot BC= DE\cdot AC$,能满足$△ADE\backsim △ACB$的条件有(
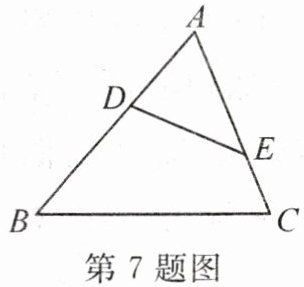
A. 1个
B. 2个
C. 3个
D. 4个
B
)
A. 1个
B. 2个
C. 3个
D. 4个
答案:
B
8. (2024·乐山)如图,在梯形ABCD中,$AD// BC$,对角线AC和BD交于点O.若$\frac {S_{△ABD}}{S_{△BCD}}= \frac {1}{3}$,则$\frac {S_{△AOD}}{S_{△BOC}}=$
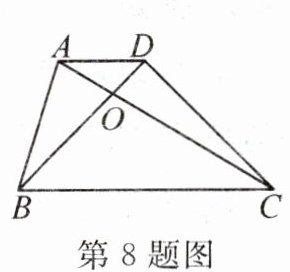
$\frac{1}{9}$
.
答案:
$\frac{1}{9}$
9. (2024·重庆)如图,在$△ABC$中,延长AC至点D,使$CD= CA$,过点D作$DE// CB$,且$DE= DC$,连接AE交BC于点F.若$∠CAB= ∠CFA,CF= 1$,则$BF= $
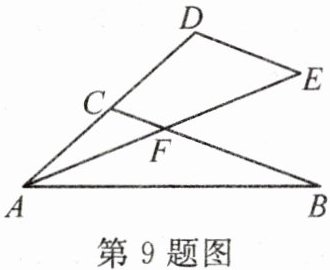
3
.
答案:
3
10. 如图,在平面直角坐标系xOy中,直线$y= 2x+4$与x轴、y轴相交于A,B两点,且点C的坐标为$(6,4)$,连接AC,与y轴相交于点D,点E在x轴上.若$△ABD和△ACE$相似,则点E的坐标为
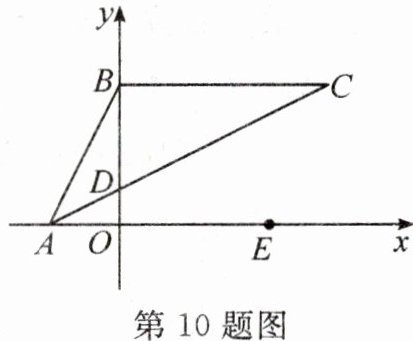
$(4,0)$或$(\frac{34}{3},0)$
.
答案:
$(4,0)$或$(\frac{34}{3},0)$
11. (2024·德阳)如图,在菱形ABCD中,$∠ABC= 60^{\circ }$,对角线AC与BD相交于点O,F为BC的中点,连接AF与BD相交于点E,连接CE并延长交AB于点G.求证:
(1)$△BEF\backsim △BCO$.
证明: ∵ 四边形 ABCD 是菱形, ∴ $AB = BC$, $AC \perp BD$. 又 ∵ $\angle ABC = 60^{\circ}$, ∴ $\triangle ABC$ 是等边三角形. ∴ $AB = AC$. ∵ F 为 BC 的中点, ∴ $AF \perp BC$. ∴ $\angle BOC = \angle BFE = 90^{\circ}$. 又 ∵ $\angle EBF = \angle CBO$, ∴ $\triangle BEF \backsim \triangle BCO$.
(2)$△BEG\cong △AEG$.
证明: ∵ $BO \perp AC$, $AF \perp BC$, ∴ $CG \perp AB$. ∴ $\angle BGE = \angle AGE$. 又 ∵ $AC = BC$, ∴ $BG = AG$. 在 $\triangle BEG$ 和 $\triangle AEG$ 中, $\left\{\begin{array}{l} BG = AG, \\ \angle BGE = \angle AGE, \\ GE = GE, \end{array}\right.$ ∴ $\triangle BEG \cong \triangle AEG$
(1)$△BEF\backsim △BCO$.
证明: ∵ 四边形 ABCD 是菱形, ∴ $AB = BC$, $AC \perp BD$. 又 ∵ $\angle ABC = 60^{\circ}$, ∴ $\triangle ABC$ 是等边三角形. ∴ $AB = AC$. ∵ F 为 BC 的中点, ∴ $AF \perp BC$. ∴ $\angle BOC = \angle BFE = 90^{\circ}$. 又 ∵ $\angle EBF = \angle CBO$, ∴ $\triangle BEF \backsim \triangle BCO$.
(2)$△BEG\cong △AEG$.
证明: ∵ $BO \perp AC$, $AF \perp BC$, ∴ $CG \perp AB$. ∴ $\angle BGE = \angle AGE$. 又 ∵ $AC = BC$, ∴ $BG = AG$. 在 $\triangle BEG$ 和 $\triangle AEG$ 中, $\left\{\begin{array}{l} BG = AG, \\ \angle BGE = \angle AGE, \\ GE = GE, \end{array}\right.$ ∴ $\triangle BEG \cong \triangle AEG$
SAS
.
答案:
证明:
(1)
∵ 四边形 ABCD 是菱形,
∴ $AB = BC$, $AC \perp BD$. 又
∵ $\angle ABC = 60^{\circ}$,
∴ $\triangle ABC$ 是等边三角形.
∴ $AB = AC$.
∵ F 为 BC 的中点,
∴ $AF \perp BC$.
∴ $\angle BOC = \angle BFE = 90^{\circ}$. 又
∵ $\angle EBF = \angle CBO$,
∴ $\triangle BEF \backsim \triangle BCO$.
(2)
∵ $BO \perp AC$, $AF \perp BC$,
∴ $CG \perp AB$.
∴ $\angle BGE = \angle AGE$. 又
∵ $AC = BC$,
∴ $BG = AG$. 在 $\triangle BEG$ 和 $\triangle AEG$ 中, $\left\{\begin{array}{l} BG = AG, \\ \angle BGE = \angle AGE, \\ GE = GE, \end{array}\right.$
∴ $\triangle BEG \cong \triangle AEG(SAS)$.
(1)
∵ 四边形 ABCD 是菱形,
∴ $AB = BC$, $AC \perp BD$. 又
∵ $\angle ABC = 60^{\circ}$,
∴ $\triangle ABC$ 是等边三角形.
∴ $AB = AC$.
∵ F 为 BC 的中点,
∴ $AF \perp BC$.
∴ $\angle BOC = \angle BFE = 90^{\circ}$. 又
∵ $\angle EBF = \angle CBO$,
∴ $\triangle BEF \backsim \triangle BCO$.
(2)
∵ $BO \perp AC$, $AF \perp BC$,
∴ $CG \perp AB$.
∴ $\angle BGE = \angle AGE$. 又
∵ $AC = BC$,
∴ $BG = AG$. 在 $\triangle BEG$ 和 $\triangle AEG$ 中, $\left\{\begin{array}{l} BG = AG, \\ \angle BGE = \angle AGE, \\ GE = GE, \end{array}\right.$
∴ $\triangle BEG \cong \triangle AEG(SAS)$.
查看更多完整答案,请扫码查看


