第75页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
1. 已知点C把线段AB分成两条线段AC,BC,且AC>BC,则下列说法错误的是 (
A. 若$\frac {AC}{AB}= \frac {BC}{AC}$,则线段AB被点C黄金分割
B. 若$AC^{2}= AB\cdot BC$,则线段AB被点C黄金分割
C. 若线段AB被点C黄金分割,则BC与AB的比叫做黄金比
D. 0.618是黄金比的近似值
C
)A. 若$\frac {AC}{AB}= \frac {BC}{AC}$,则线段AB被点C黄金分割
B. 若$AC^{2}= AB\cdot BC$,则线段AB被点C黄金分割
C. 若线段AB被点C黄金分割,则BC与AB的比叫做黄金比
D. 0.618是黄金比的近似值
答案:
C
2. 已知C是线段AB的黄金分割点,AC>BC.若AB= 2,则AC的长为
$\sqrt{5}-1$
.(结果保留根号)
答案:
$\sqrt{5}-1$
3. 如图,在设计人体雕像时,使雕像的腰部以下a与全身b的高度比值接近0.618,可以增加视觉美感.若图中b为2m,则a约为(结果保留两位小数) (
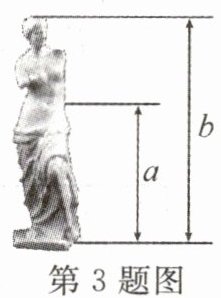
A. 1.24m
B. 1.38m
C. 1.42m
D. 1.62m
A
)
A. 1.24m
B. 1.38m
C. 1.42m
D. 1.62m
答案:
A
4. 新考向 跨学科(2024·山西)黄金分割是汉字结构最基本的规律.借助如图所示的正方形习字格书写的汉字“晋”端庄稳重、舒展美观.已知一条分割线的端点A,B分别在习字格的边MN,PQ上,且AB//NP,“晋”字的笔画“、”的位置在AB的黄金分割点C处,且$\frac {BC}{AB}= \frac {\sqrt {5}-1}{2}$.若NP= 2cm,则BC的长为
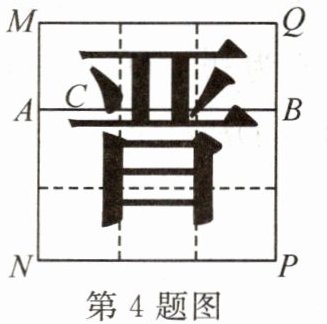
$(\sqrt {5}-1)$
cm(结果保留根号).
答案:
$(\sqrt {5}-1)$
5. 已知线段MN的长为1cm,P是MN的黄金分割点,则MP的长是
$\frac{\sqrt{5}-1}{2}cm$ 或 $\frac{3-\sqrt{5}}{2}cm$
.(结果保留根号)
答案:
$\frac{\sqrt{5}-1}{2}cm$ 或 $\frac{3-\sqrt{5}}{2}cm$
6. (2023·绵阳)黄金分割由于其美学性质,受到摄影爱好者和艺术家的喜爱.摄影中有一种拍摄手法叫黄金构图法,其原理是:如图,在正方形ABCD的底边BC上取中点E,以点E为圆心,线段DE为半径作圆,其与底边BC的延长线相交于点F,这样就把正方形ABCD延伸为矩形ABFG,称其为黄金矩形(宽与长的比等于$\frac {\sqrt {5}-1}{2}$的矩形叫作黄金矩形).若CF= 4a,则AB= (
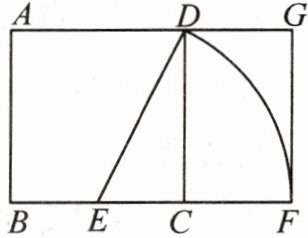
A. $(\sqrt {5}-1)a$
B. $(2\sqrt {5}-2)a$
C. $(\sqrt {5}+1)a$
D. $(2\sqrt {5}+2)a$
D
)
A. $(\sqrt {5}-1)a$
B. $(2\sqrt {5}-2)a$
C. $(\sqrt {5}+1)a$
D. $(2\sqrt {5}+2)a$
答案:
D
7. (2023·达州)如图,乐器上的一根弦AB= 80cm,两个端点A,B固定在乐器面板上,支撑点C是靠近点B的黄金分割点,支撑点D是靠近点A的黄金分割点,则支撑点C,D之间的距离为
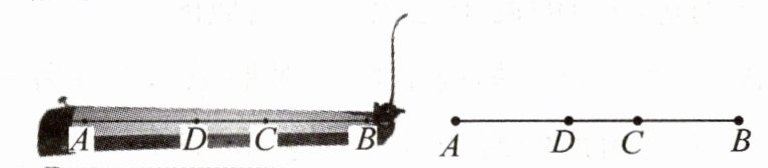
$(80\sqrt{5}-160)$
cm.(结果保留根号)
答案:
$(80\sqrt{5}-160)$
8. 如图,已知△ABC,用尺规作图法按如下步骤作图:①以点C为圆心,任意长为半径画弧,分别交BC,AC于点M,N;②以点A为圆心,CM的长为半径画弧,交AB于点P;③以点P为圆心,MN的长为半径画弧,两弧相交于点Q;④连接AQ并延长,与CB的延长线交于点D.若AD= BC,请解答下列问题:(1)求证:B为线段CD的黄金分割点.证明: 由作图步骤可得, ∠BAD=∠C. ∵∠D=∠D, ∴
△ABD∽△CAD
. ∴AD/CD=BD/AD
. ∵AD=BC, ∴BC/CD=BD/BC
. ∴B为线段CD的黄金分割点.(2)若AD= 20cm,求CD的长.(结果保留根号)解:由(1)可知,B为线段CD的黄金分割点,∴BC/CD=(√5-1)/2
.∵BC=AD=20cm,∴CD=(10√5+10)
cm.
答案:
解:
(1) 证明: 由作图步骤可得, $∠BAD=∠C$. $\because ∠D=∠D$, $\therefore$
$△ABD \backsim △CAD$. $\therefore \frac{AD}{CD}=\frac{BD}{AD}$. $\because AD=BC$, $\therefore \frac{BC}{CD}=\frac{BD}{BC}$. $\therefore B$ 为线段 $CD$ 的黄金分割点.
(2) 由
(1) 可知, $B$ 为线段 $CD$ 的黄金分割点, $\therefore \frac{BC}{CD}=\frac{\sqrt{5}-1}{2}$. $\because BC=AD=20cm$, $\therefore CD=\frac{2}{\sqrt{5}-1}BC=\frac{\sqrt{5}+1}{2}×20=(10\sqrt{5}+10)cm$.
(1) 证明: 由作图步骤可得, $∠BAD=∠C$. $\because ∠D=∠D$, $\therefore$
$△ABD \backsim △CAD$. $\therefore \frac{AD}{CD}=\frac{BD}{AD}$. $\because AD=BC$, $\therefore \frac{BC}{CD}=\frac{BD}{BC}$. $\therefore B$ 为线段 $CD$ 的黄金分割点.
(2) 由
(1) 可知, $B$ 为线段 $CD$ 的黄金分割点, $\therefore \frac{BC}{CD}=\frac{\sqrt{5}-1}{2}$. $\because BC=AD=20cm$, $\therefore CD=\frac{2}{\sqrt{5}-1}BC=\frac{\sqrt{5}+1}{2}×20=(10\sqrt{5}+10)cm$.
查看更多完整答案,请扫码查看


