第82页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
1. 已知$\triangle ABC \backsim \triangle DEF$,若$\triangle ABC与\triangle DEF的相似比为\frac{3}{4}$,则$\triangle ABC与\triangle DEF$对应中线的比为 (
A. $\frac{3}{4}$
B. $\frac{4}{3}$
C. $\frac{9}{16}$
D. $\frac{16}{9}$
A
)A. $\frac{3}{4}$
B. $\frac{4}{3}$
C. $\frac{9}{16}$
D. $\frac{16}{9}$
答案:
A
2. 如图,已知$\triangle ADE \backsim \triangle ABC$,相似比为$1:3$,过点$A作AG \perp BC于点G$,交$DE于点F$,则$AF:FG= $ (
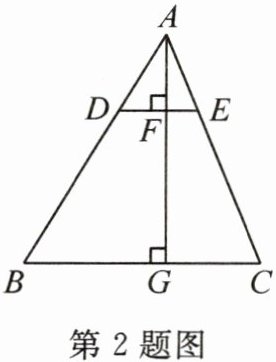
A. $1:3$
B. $3:1$
C. $1:2$
D. $2:1$
C
)
A. $1:3$
B. $3:1$
C. $1:2$
D. $2:1$
答案:
C
3. 已知$\triangle ABC \backsim \triangle DEF$,且相似比为$4:3$。若$\triangle ABC中\angle BAC的平分线AM= 8$,则$\triangle DEF中\angle EDF的平分线DN= $
6
。
答案:
6
4. 已知$\triangle ABC \backsim \triangle A'B'C'$,$AD$,$BE分别是\triangle ABC$的高和中线,$A'D'$,$B'E'分别是\triangle A'B'C'$的高和中线,且$AD= 4$,$A'D'= 3$。若$BE= 6$,则$B'E'$的长为
$\frac{9}{2}$
。
答案:
$\frac{9}{2}$
5. 如图,在$\triangle ABC$中,$D$,$E分别是AB$,$AC$的中点,$\angle BAC的平分线分别交DE$,$BC于点G$,$F$,则$AG:AF$的值为
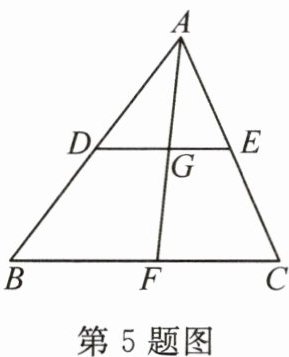
$\frac{1}{2}$
。
答案:
$\frac{1}{2}$
6. 如图,在$\triangle ABC$中,$D$,$E分别是\triangle ABC的边AB$,$AC$上的点,$DE // BC$,$CF$,$EG分别是\triangle ABC与\triangle ADE$的中线,已知$AD:DB= 4:3$,$EG= 4cm$,求$CF$的长。
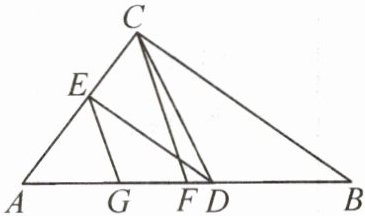
解: $\because AD:DB = 4:3$, $\therefore AD:AB = 4:7$. $\because DE// BC$, $\therefore \angle ADE = \angle B$, $\angle AED = \angle ACB$. $\therefore \triangle ADE\backsim\triangle ABC$. $\because CF$, $EG$分别是$\triangle ABC$与$\triangle ADE$的中线, $\therefore \frac{AD}{AB} = \frac{EG}{CF}$, 即$\frac{4}{7} = \frac{4}{CF}$. $\therefore CF =$

解: $\because AD:DB = 4:3$, $\therefore AD:AB = 4:7$. $\because DE// BC$, $\therefore \angle ADE = \angle B$, $\angle AED = \angle ACB$. $\therefore \triangle ADE\backsim\triangle ABC$. $\because CF$, $EG$分别是$\triangle ABC$与$\triangle ADE$的中线, $\therefore \frac{AD}{AB} = \frac{EG}{CF}$, 即$\frac{4}{7} = \frac{4}{CF}$. $\therefore CF =$
7
$cm$.
答案:
解: $\because AD:DB = 4:3$, $\therefore AD:AB = 4:7$. $\because DE// BC$, $\therefore \angle ADE = \angle B$, $\angle AED = \angle ACB$. $\therefore \triangle ADE\backsim\triangle ABC$. $\because CF$, $EG$分别是$\triangle ABC$与$\triangle ADE$的中线, $\therefore \frac{AD}{AB} = \frac{EG}{CF}$, 即$\frac{4}{7} = \frac{4}{CF}$. $\therefore CF = 7cm$.
7. (教材P108习题T2变式)如图所示的是步枪在瞄准时的示意图,从眼睛到准星的距离$OE为80cm$,步枪上的准星宽度$AB为0.2cm$,目标的正面宽度$CD为50cm$,则眼睛到目标的距离$OF$是 (
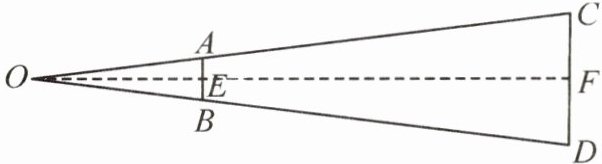
A. $20000m$
B. $400m$
C. $200m$
D. $199.2m$
C
)
A. $20000m$
B. $400m$
C. $200m$
D. $199.2m$
答案:
C
8. 如图,光源$P在横杆AB$的正上方,$AB在灯光下的影子为CD$,$AB // CD$,$AB= 2m$,$CD= 6m$,点$P到CD的距离是2.7m$,则$AB与CD$的距离为

1.8
$m$。
答案:
1.8
9. 新考向 跨学科 小孔成像是光在均匀介质中沿直线传播形成的一种物理现象。两千四百多年前,我国学者墨子就在《墨经》中记载了小孔成像实验的做法与成因,图1是某次小孔成像实验图,抽象为数学问题如图2:$AC与BD交于点O$,$AB // CD$。若点$O到AB的距离为10cm$,点$O到CD的距离为15cm$,蜡烛火焰$AB的高度是3cm$,则蜡烛火焰倒立的像$CD$的高度是 (
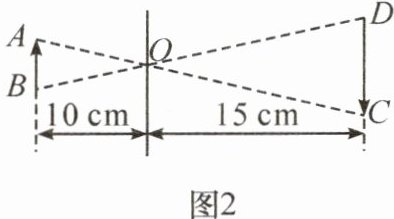
A. $2cm$
B. $\frac{9}{2}cm$
C. $\frac{15}{2}cm$
D. $9cm$
B
)

A. $2cm$
B. $\frac{9}{2}cm$
C. $\frac{15}{2}cm$
D. $9cm$
答案:
B
查看更多完整答案,请扫码查看


