《2025年名校课堂九年级数学上册北师大版》

9. 现有下列四个条件：①$∠ABC= 90^{\circ}$；②$AB= BC$；③$AC= BD$；④$AC⊥BD$.从中选择两个作为补充条件,使平行四边形ABCD成为正方形,下列四种情况,你认为错误的是(B)
A. ①②
B. ①③
C. ②③
D. ③④

答案： B

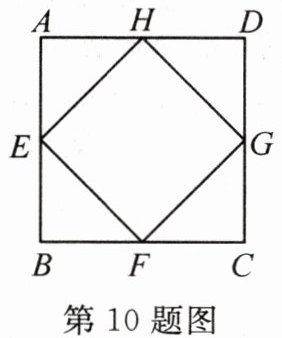
10. (2024·福建)如图,正方形ABCD的面积为4,E,F,G,H分别为边AB,BC,CD,AD的中点,则四边形EFGH的面积为2.

答案： 2

11. 如图,在矩形ABCD中,M,N分别是边AD,BC的中点,E,F分别是边BM,CM的中点.当$AB:AD=$1:2时,四边形MENF是正方形.

答案： 1:2

12. 如图,在矩形ABCD中,E是边BC上一点,DE平分∠ADC,EF// DC交边AD于点F,连接BD.
(1)求证：四边形EFDC是正方形.

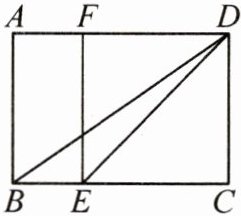
证明:∵四边形ABCD是矩形,∴AD//BC,∠ADC=∠C=90°.∵EF//DC,∴∠FEC=90°.∴四边形EFDC是矩形.∵DE平分∠ADC,∴∠EDC=$\frac{1}{2}$∠ADC=45°.∵∠C=90°,∴∠DEC=90°−45°=45°=∠EDC.∴CE=CD.∴矩形EFDC是正方形.
(2)若BE= 1,ED= 2$\sqrt{2}$,求BD的长.
解:∵四边形EFDC是正方形，∴∠CDE=45°.∵ED=2$\sqrt{2}$,∴CE=CD=2.∴BC=BE+EC=1+2=3.∴BD=√(BC²+CD²)=$\sqrt{3²+2²}$=$\sqrt{13}$

答案： 解:
(1)证明:
∵四边形ABCD是矩形,
∴AD//BC,∠ADC=∠C=90°.
∵EF//DC,
∴∠FEC=90°.
∴四边形EFDC是矩形.
∵DE平分∠ADC,
∴∠EDC=$\frac{1}{2}$∠ADC=45°.
∵∠C=90°,
∴∠DEC=90°−45°=45°=∠EDC.
∴CE=CD.
∴矩形EFDC是正方形.
(2)
∵四边形EFDC是正方形，
∴∠CDE=45°.
∵ED=2$\sqrt{2}$,
∴CE=CD=2.
∴BC=BE+EC=1+2=3.
∴BD=√(BC²+CD²)=$\sqrt{3²+2²}$=$\sqrt{13}$

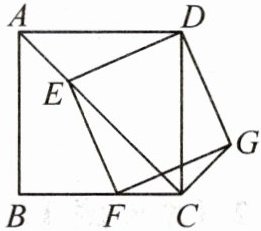
13. 如图,四边形ABCD为正方形,E为线段AC上一点,连接DE,过点E作$EF⊥DE$,交射线BC于点F,以DE,EF为邻边作矩形DEFG,连接CG.
(1)求证：矩形DEFG是正方形.
(2)若$AB= 4$,$CE= 2\sqrt{2}$,求CG的长.
(3)当线段DE与正方形ABCD的某条边的夹角是$40^{\circ}$时,直接写出$∠EFC$的度数.

答案：
解:
(1)证明:过点E作EP⊥CD于点P,EQ⊥BC于点Q,
∵∠DCA=∠BCA,
∴EQ=EP.易证四边形EQCP是正方形,
∴∠QEP=∠FED=90°.
∴∠QEP−∠FEP=∠FED−∠FEP,即∠QEF=∠PED.在△EQF和△EPD中,{∠QEF = ∠PED, EQ = EP, ∠EQF = ∠EPD}，
∴△EQF≌△EPD(ASA).
∴EF=ED.
∴矩形DEFG是正方形.
(2)在Rt△ABC中,AC=√2AB=4√2;
∵CE=2√2,
∴AE=CE=2√2.
∴点F与点C重合,此时△DCE是等腰直角三角形,如图.
∴四边形DECG是正方形
∴CG=CE=2$\sqrt{2}$.
(3)∠EFC=130°或40°.