《2025年名校课堂九年级数学上册北师大版》

1. (教材P80随堂练习变式)如果$\frac {a}{b}= \frac {c}{d}= \frac {e}{f}= \frac {1}{3}$($a,b,c,d,e,f$均为正数),那么下列选项中错误的是 (D)
A. $\frac {a+c}{b+d}= \frac {1}{3}$
B. $\frac {a+e}{b+f}= \frac {1}{3}$
C. $\frac {a+c+e}{b+d+f}= \frac {1}{3}$
D. $\frac {a}{b}= \frac {c+m}{d+m}(m＞0)$

答案： D

2. 已知$\frac {a}{b}= \frac {c}{d}= \frac {e}{f}= \frac {4}{3}$,若$b+d+f= 9$,则$a+c+e= $12.

答案： 12

3. 若$\frac {a}{b}= \frac {2}{3}(b≠-6)$,则$\frac {a+4}{b+6}$的值为$\frac{2}{3}$.

答案： $\frac{2}{3}$

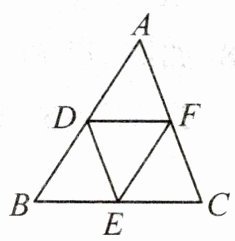
4. (教材P80例2变式)如图,在$\triangle ABC$中,$D,E,F分别为AB$,$BC$,$AC$的中点,连接$DE$,$DF$,$EF$,则$\frac {DE+EF+DF}{AC+AB+BC}$的值为$\frac{1}{2}$.

答案： $\frac{1}{2}$

5. 若$\frac {a-b}{b}= \frac {3}{5}$,则$\frac {a}{b}$的值为 (C)
A. $\frac {3}{8}$
B. $\frac {3}{5}$
C. $\frac {8}{5}$
D. $\frac {5}{3}$

答案： C

6. (教材P81习题T3变式)若$\frac {y}{x}= 2$,则$\frac {x+y}{x}$的值为3.

答案： 3

7. 已知$\frac {a}{b}= \frac {c}{d}= \frac {e}{f}= \frac {3}{4}$,则$\frac {a+c-2e}{b+d-2f}(b+d-2f≠0)$的值为$\frac{3}{4}$,$\frac {a-2c+3e}{2b-4d+6f}(2b-4d+6f≠0)$的值为$\frac{3}{8}$.

答案： $\frac{3}{4}$ $\frac{3}{8}$

8. 若$\frac {x}{2}= \frac {y}{3}= \frac {z}{4}$,且$x+2y+z= 36$,则$x=$6,$y=$9,$z=$12.

答案： 6 9 12

9. 已知$a,b,c是\triangle ABC$的三边长,满足$\frac {a+4}{3}= \frac {b+3}{2}= \frac {c+8}{4}$,且$a+b+c= 12$,请探索$\triangle ABC$的形状.
解:由等比性质,得$\frac{a + 4}{3} = \frac{b + 3}{2} = \frac{c + 8}{4} = \frac{a + 4 + b + 3 + c + 8}{3 + 2 + 4}$,$\because$
$a + b + c = 12$,$\therefore \frac{a + 4}{3} = \frac{b + 3}{2} = \frac{c + 8}{4} = \frac{12 + 4 + 3 + 8}{3 + 2 + 4} = 3$.$\therefore a + 4$
$= 9$,$b + 3 = 6$,$c + 8 = 12$.$\therefore a = 5$,$b = 3$,$c = 4$.$\because b^{2} + c^{2} = 3^{2} + 4^{2}$
$= 25 = a^{2}$,$\therefore \triangle ABC$是直角三角形.

答案： 解:由等比性质,得$\frac{a + 4}{3} = \frac{b + 3}{2} = \frac{c + 8}{4} = \frac{a + 4 + b + 3 + c + 8}{3 + 2 + 4}$,$\because$
$a + b + c = 12$,$\therefore \frac{a + 4}{3} = \frac{b + 3}{2} = \frac{c + 8}{4} = \frac{12 + 4 + 3 + 8}{3 + 2 + 4} = 3$.$\therefore a + 4$
$= 9$,$b + 3 = 6$,$c + 8 = 12$.$\therefore a = 5$,$b = 3$,$c = 4$.$\because b^{2} + c^{2} = 3^{2} + 4^{2}$
$= 25 = a^{2}$,$\therefore \triangle ABC$是直角三角形.

10. 若$\frac {a+b}{c}= \frac {b+c}{a}= \frac {c+a}{b}= k$,则$k$的值为2 或 -1.

答案： 2 或 -1

11. 新考向 推理能力(本课时T10变式)已知$a,b,c$均为非零的实数,且满足$\frac {a+b-c}{c}= \frac {a-b+c}{b}= \frac {-a+b+c}{a}$,求$\frac {(a+b)(b+c)(c+a)}{abc}$的值.8 或 -1

答案： 解:①当$a + b + c \neq 0$时,由等比性质,得$\frac{a + b - c}{c} = \frac{a - b + c}{b} =$
$\frac{-a + b + c}{a} = \frac{a + b - c + a - b + c - a + b + c}{a + b + c} = 1$,$\therefore a + b - c = c$,$a$
$-b + c = b$,$-a + b + c = a$.$\therefore a + b = 2c$,$a + c = 2b$,$b + c = 2a$.$\therefore$
$\frac{(a + b)(b + c)(c + a)}{abc} = \frac{2c \cdot 2a \cdot 2b}{abc} = 8$. ②当$a + b + c = 0$时,$a$
$+ b = -c$,$b + c = -a$,$c + a = -b$,$\therefore \frac{(a + b)(b + c)(c + a)}{abc} =$
$\frac{(-c)(-a)(-b)}{abc} = -1$. 综上所述,$\frac{(a + b)(b + c)(c + a)}{abc}$的值
为 8 或 -1.