第27页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
1. 下列各数中,是方程$x^{2}-x= 2$的根的是(
A. 1
B. 0
C. -1
D. -2
C
)A. 1
B. 0
C. -1
D. -2
答案:
C
2. (2024·深圳)已知一元二次方程$x^{2}-4x+a= 0$的一个解为$x= 1$,则$a=$
3
.
答案:
3
3. 【整体思想】已知a是一元二次方程$x^{2}-2x-4= 0$的一个根,则代数式$a^{2}-2a+2024$的值为
2028
.
答案:
2 028
4. 根据下面表格中的对应值,判断关于x的方程$ax^{2}+bx+c= 0(a≠0)$的一个解x的取值范围是(
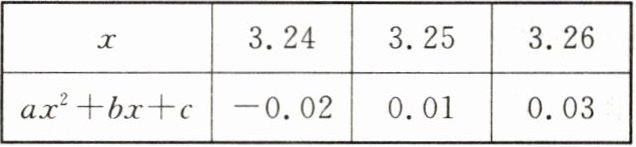
A. $x<3.24$
B. $3.24<x<3.25$
C. $3.25<x<3.26$
D. $x>3.26$
B
)
A. $x<3.24$
B. $3.24<x<3.25$
C. $3.25<x<3.26$
D. $x>3.26$
答案:
B
5. (教材P33“做一做”变式)“一块矩形铁片,面积为$10m^{2}$,长比宽多4m,求铁片的长.”小颖在做这道题时,是这样考虑的:设铁片的长为xm,列出方程为$x(x-4)= 10$,整理,得$x^{2}-4x-10= 0$.小颖列出方程后,想知道铁片的长到底是多少,下面是她的探索过程.
第一步:

所以____<x<____.
第二步:

所以____<x<____.
(1)请你帮小颖完成她未完成的部分.
(2)通过以上探索,可以估计矩形铁片长的整数部分是____,十分位是____.
(1)
(2)
第一步:

所以____<x<____.
第二步:

所以____<x<____.
(1)请你帮小颖完成她未完成的部分.
(2)通过以上探索,可以估计矩形铁片长的整数部分是____,十分位是____.
(1)
5
6
5.7
5.8
(2)
5
7
答案:
(1) 5 6 5.7 5.8
(2) 5 7
(1) 5 6 5.7 5.8
(2) 5 7
6. (2024·凉山州)若关于x的一元二次方程$(a+2)x^{2}+x+a^{2}-4= 0$的一个根是x= 0,则a的值为(
A. 2
B. -2
C. 2或-2
D. $\frac{1}{2}$
A
)A. 2
B. -2
C. 2或-2
D. $\frac{1}{2}$
答案:
A
7. 观察下列表格,一元二次方程$x^{2}-x= 1.1$的一个近似解可能是(

A. 0.9
B. 1.58
C. 1.66
D. 1.73
C
)
A. 0.9
B. 1.58
C. 1.66
D. 1.73
答案:
C
8. 新考向 开放性问题 构造一个一元二次方程,要求:①常数项不为0;②有一个根为-1.这个一元二次方程可以是
$x^{2}-1=0$
(写出一个即可).
答案:
答案不唯一,如:$x^{2}-1=0$
9. 已知一元二次方程$ax^{2}+ax-4= 0$有一个根是-2,则一次函数$y= ax-3$的图象不经过第
二
象限.
答案:
二
10. 已知一元二次方程$ax^{2}+bx+c= 0$.若方程有一个根为-1,则$a-b+c=$
0
;若$a+b+c= 0$,则方程有一个根为1
.
答案:
0 1
11. 【整体思想】若a是方程$x^{2}-2024x+1= 0$的一个根,则代数式$a^{2}-2025a+\frac{a^{2}+1}{2024}$的值为
-1
.
答案:
-1
查看更多完整答案,请扫码查看


