第2页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
1. 如图,在$□ ABCD$中,$\because AB = AD$,$\therefore □ ABCD$是菱形(
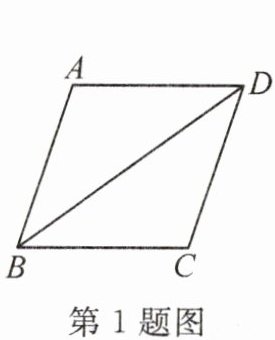
有一组邻边相等的平行四边形是菱形
). (请在横线上填写依据)
答案:
有一组邻边相等的平行四边形是菱形
2. 如图,在菱形$OABC$中,点$B在x$轴上,点$A的坐标为(2,3)$,则点$C$的坐标为
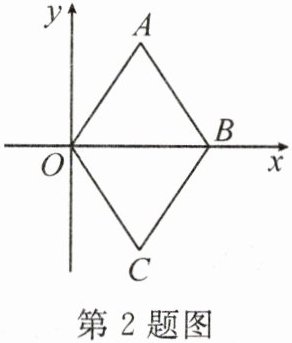
$(2,-3)$
,点$B$的坐标为$(4,0)$
.
答案:
$(2,-3)$ $(4,0)$
3. (2024·甘孜州)如图,在菱形$ABCD$中,$AB = 2$,则菱形$ABCD$的周长为
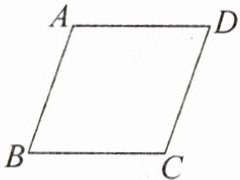
8
.
答案:
8
4. (2024·上海)在菱形$ABCD$中,$\angle ABC = 66^{\circ}$,则$\angle BAC = $
$57^{\circ}$
.
答案:
$57^{\circ}$
5. (2024·福建)如图,在菱形$ABCD$中,点$E$,$F分别在边BC和CD$上,且$\angle AEB = \angle AFD$. 求证:$BE = DF$.
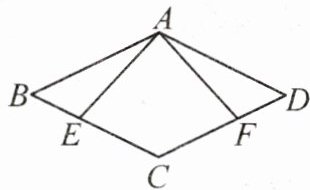
证明:∵ 四边形 ABCD 是菱形,$\therefore AB=AD,∠B=∠D$. 在$\triangle ABE$和$\triangle ADF$中,$\left\{\begin{array}{l} ∠B=∠D,\\ ∠AEB=∠AFD,\\ AB=AD,\end{array}\right. $$\therefore \triangle ABE\cong \triangle ADF$(

证明:∵ 四边形 ABCD 是菱形,$\therefore AB=AD,∠B=∠D$. 在$\triangle ABE$和$\triangle ADF$中,$\left\{\begin{array}{l} ∠B=∠D,\\ ∠AEB=∠AFD,\\ AB=AD,\end{array}\right. $$\therefore \triangle ABE\cong \triangle ADF$(
AAS
).$\therefore BE=DF.$
答案:
证明:
∵ 四边形 ABCD 是菱形,$\therefore AB=AD,∠B=∠D$. 在$\triangle ABE$和$\triangle ADF$中,$\left\{\begin{array}{l} ∠B=∠D,\\ ∠AEB=∠AFD,\\ AB=AD,\end{array}\right. $$\therefore \triangle ABE\cong \triangle ADF$(AAS).$\therefore BE=DF.$
∵ 四边形 ABCD 是菱形,$\therefore AB=AD,∠B=∠D$. 在$\triangle ABE$和$\triangle ADF$中,$\left\{\begin{array}{l} ∠B=∠D,\\ ∠AEB=∠AFD,\\ AB=AD,\end{array}\right. $$\therefore \triangle ABE\cong \triangle ADF$(AAS).$\therefore BE=DF.$
6. 菱形具有而一般平行四边形不具有的性质是(
A. 对边平行
B. 对边相等
C. 对角线互相平分
D. 对角线互相垂直
D
)A. 对边平行
B. 对边相等
C. 对角线互相平分
D. 对角线互相垂直
答案:
D
7. 如图,在菱形$ABCD$中,连接$AC$,$BD$. 若$\angle 1 = 20^{\circ}$,则$\angle 2$的度数为(
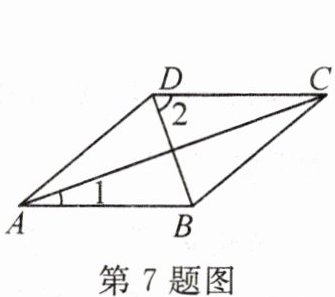
A. $20^{\circ}$
B. $60^{\circ}$
C. $70^{\circ}$
D. $80^{\circ}$
C
)
A. $20^{\circ}$
B. $60^{\circ}$
C. $70^{\circ}$
D. $80^{\circ}$
答案:
C
8. 如图,在菱形$ABCD$中,对角线$AC$,$BD相交于点O$,$E为CD$的中点. 若$OE = 3$,则菱形$ABCD$的周长为
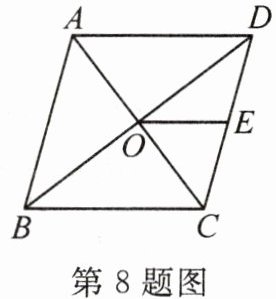
24
.
答案:
24
9. 菱形$ABCD的周长为40\mathrm{cm}$,它的一条对角线长为$10\mathrm{cm}$,则此菱形另一条对角线长为
$10\sqrt {3}$
$\mathrm{cm}$.
答案:
$10\sqrt {3}$
10. (教材P3例1变式)如图,四边形$ABCD$是菱形,$\angle ACD = 30^{\circ}$,$BD = 6$.
(1)$\angle BAD = $
(2)求$AB和AC$的长.
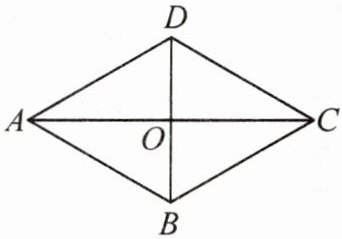
(1)$\angle BAD = $
60
$^{\circ}$,$\angle ABC = $120
$^{\circ}$.(2)求$AB和AC$的长.

解:(2)∵ 四边形 ABCD 是菱形,$\therefore AB=DC,AC$$⊥BD,OD=\frac {1}{2}BD=3,AC=2OC$. 在$Rt\triangle OCD$中,$∠ACD=$$30^{\circ },\therefore DC=2OD=6,OC=\sqrt {DC^{2}-OD^{2}}=\sqrt {6^{2}-3^{2}}=3\sqrt {3}.$$\therefore AB=DC=6,AC=2OC=6\sqrt {3}.$
答案:
解:
(1)60 120
(2)
∵ 四边形 ABCD 是菱形,$\therefore AB=DC,AC$$⊥BD,OD=\frac {1}{2}BD=3,AC=2OC$. 在$Rt\triangle OCD$中,$∠ACD=$$30^{\circ },\therefore DC=2OD=6,OC=\sqrt {DC^{2}-OD^{2}}=\sqrt {6^{2}-3^{2}}=3\sqrt {3}.$$\therefore AB=DC=6,AC=2OC=6\sqrt {3}.$
(1)60 120
(2)
∵ 四边形 ABCD 是菱形,$\therefore AB=DC,AC$$⊥BD,OD=\frac {1}{2}BD=3,AC=2OC$. 在$Rt\triangle OCD$中,$∠ACD=$$30^{\circ },\therefore DC=2OD=6,OC=\sqrt {DC^{2}-OD^{2}}=\sqrt {6^{2}-3^{2}}=3\sqrt {3}.$$\therefore AB=DC=6,AC=2OC=6\sqrt {3}.$
查看更多完整答案,请扫码查看


