第98页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
14. 如图,四个三角形拼成一个风车图形.若$AB= 2$,当风车转动$90^{\circ }$时,点B转动的路径长为(
A.π
B.2π
C.3π
D.4π
A
)A.π
B.2π
C.3π
D.4π
答案:
解:由题意知,点B绕点A旋转,AB的长度为旋转半径,即$r = AB = 2$。
风车转动$90^{\circ}$,则点B转动的圆心角$n = 90^{\circ}$。
根据弧长公式$l=\frac{n\pi r}{180}$,可得点B转动的路径长为:
$l=\frac{90\pi×2}{180}=\pi$
答案:A
风车转动$90^{\circ}$,则点B转动的圆心角$n = 90^{\circ}$。
根据弧长公式$l=\frac{n\pi r}{180}$,可得点B转动的路径长为:
$l=\frac{90\pi×2}{180}=\pi$
答案:A
15. (2024·资阳)如图,在矩形ABCD中,$AB= 4,AD= 2$.以点A为圆心,AD为半径画弧,交AB于点E,再以AB为直径作半圆,与$\widehat {DE}$交于点F,则图中涂色部分的面积为____.
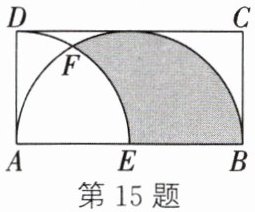

2
答案:
解:连接AF,OF。
在矩形ABCD中,AB=4,AD=2,AE=AD=2,AB为直径,OA=OB=OF=2。
在Rt△AOF中,OA=OF=2,∠OAF=45°,S△AOF=2。
S扇形OAF= $\frac{45\pi×2^2}{360}=\frac{\pi}{2}$。
S扇形DAE= $\frac{90\pi×2^2}{360}=\pi$。
S半圆= $\frac{1}{2}\pi×2^2=2\pi$。
涂色部分面积=S半圆 - (S扇形DAE - S△AOF + S扇形OAF)= $2\pi - (\pi - 2 + \frac{\pi}{2})=2$。
答案:2
在矩形ABCD中,AB=4,AD=2,AE=AD=2,AB为直径,OA=OB=OF=2。
在Rt△AOF中,OA=OF=2,∠OAF=45°,S△AOF=2。
S扇形OAF= $\frac{45\pi×2^2}{360}=\frac{\pi}{2}$。
S扇形DAE= $\frac{90\pi×2^2}{360}=\pi$。
S半圆= $\frac{1}{2}\pi×2^2=2\pi$。
涂色部分面积=S半圆 - (S扇形DAE - S△AOF + S扇形OAF)= $2\pi - (\pi - 2 + \frac{\pi}{2})=2$。
答案:2
16. 如图,在扇形OAB中,$OA= OB= 2,∠AOB= 90^{\circ }$,C为$\widehat {AB}$上一点,$∠AOC= 30^{\circ }$,连接BC,过点C作OA的垂线,垂足为D,求涂色部分的面积.
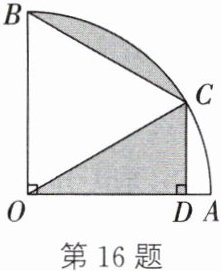

答案:
解:
∵∠AOB=90°,∠AOC=30°,
∴∠BOC=∠AOB-∠AOC=60°.
∵OA=OB=OC=2,CD⊥OA,∠AOC=30°,
∴CD=OC·sin30°=2×$\frac{1}{2}$=1,OD=OC·cos30°=2×√$\frac{3}{2}$=√3.
S扇形BOC=60π×2²/360=2π/3,
S△COD=$\frac{1}{2}$×OD×CD=$\frac{1}{2}$×√3×1=√$\frac{3}{2}$,
涂色部分面积=S扇形BOC+S△COD=2π/3+√$\frac{3}{2}$.
答:涂色部分的面积为2π/3+√$\frac{3}{2}$.
∵∠AOB=90°,∠AOC=30°,
∴∠BOC=∠AOB-∠AOC=60°.
∵OA=OB=OC=2,CD⊥OA,∠AOC=30°,
∴CD=OC·sin30°=2×$\frac{1}{2}$=1,OD=OC·cos30°=2×√$\frac{3}{2}$=√3.
S扇形BOC=60π×2²/360=2π/3,
S△COD=$\frac{1}{2}$×OD×CD=$\frac{1}{2}$×√3×1=√$\frac{3}{2}$,
涂色部分面积=S扇形BOC+S△COD=2π/3+√$\frac{3}{2}$.
答:涂色部分的面积为2π/3+√$\frac{3}{2}$.
17. 如图,在$\odot O$中,P为优弧AB上一个动点(不与A,B两点重合),$PQ⊥AB$,垂足为Q,D是线段BP的中点,连接DQ.若$\odot O$的半径为4,则DQ长的最大值是 (
A.4
B.$4\sqrt {2}$
C.6
D.8
A
)A.4
B.$4\sqrt {2}$
C.6
D.8
答案:
解:连接AP。
∵PQ⊥AB,
∴∠PQB=90°。
∵D是BP中点,直角三角形斜边上的中线等于斜边一半,
∴DQ=1/2 BP。
要使DQ最大,需BP最大。
BP为⊙O的弦,当BP为直径时最大,
∵⊙O半径为4,
∴直径为8,即BP最大值为8。
∴DQ最大值=1/2×8=4。
答案:A
∵PQ⊥AB,
∴∠PQB=90°。
∵D是BP中点,直角三角形斜边上的中线等于斜边一半,
∴DQ=1/2 BP。
要使DQ最大,需BP最大。
BP为⊙O的弦,当BP为直径时最大,
∵⊙O半径为4,
∴直径为8,即BP最大值为8。
∴DQ最大值=1/2×8=4。
答案:A
18. (2023·启东期中)如图,$△ABC$是边长为3的等边三角形,$\odot A$的半径为1,D是边BC上一动点,DM,DN分别切$\odot A$于点M,N,$\odot A$的另一条切线分别交DM,DN于点E,F,则$△DEF$的周长l的取值范围是 (
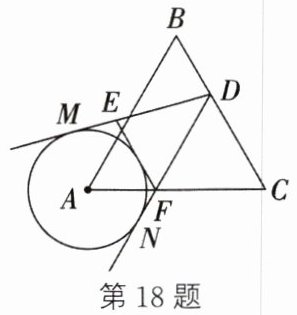
A.$4\sqrt {2}≤l≤6$
B.$4≤l≤\sqrt {23}$
C.$\sqrt {23}≤l≤4\sqrt {2}$
D.$4\sqrt {2}≤l≤2\sqrt {10}$
C
)
A.$4\sqrt {2}≤l≤6$
B.$4≤l≤\sqrt {23}$
C.$\sqrt {23}≤l≤4\sqrt {2}$
D.$4\sqrt {2}≤l≤2\sqrt {10}$
答案:
解:连接AM,AN,设EF切$\odot A$于点P,AD与MN交于点Q。
$\because DM,DN,EF$是$\odot A$的切线,$\therefore EM=EP,FN=FP,AM\perp DM,AN\perp DN$。
$\triangle DEF$的周长$l=DE+DF+EF=DE+DF+EP+FP=DE+EM+DF+FN=DM+DN$。
$\because \triangle ABC$是等边三角形,边长为3,$\odot A$半径为1,$\therefore AM=AN=1$。
设$AD=x$,在$Rt\triangle AMD$中,$DM=\sqrt{AD^2 - AM^2}=\sqrt{x^2 - 1}$,同理$DN=\sqrt{x^2 - 1}$,$\therefore l=2\sqrt{x^2 - 1}$。
当D在BC上运动时,AD的最小值为A到BC的距离,即$\frac{\sqrt{3}}{2}×3=\frac{3\sqrt{3}}{2}\approx2.598$,最大值为AB或AC的长3。
$\therefore x_{\text{min}}=\frac{3\sqrt{3}}{2}$,$x_{\text{max}}=3$。
当$x=\frac{3\sqrt{3}}{2}$时,$l=2\sqrt{(\frac{3\sqrt{3}}{2})^2 - 1}=2\sqrt{\frac{27}{4}-1}=2\sqrt{\frac{23}{4}}=\sqrt{23}\approx4.796$;
当$x=3$时,$l=2\sqrt{3^2 - 1}=2\sqrt{8}=4\sqrt{2}\approx5.656$。
$\therefore \sqrt{23}\leq l\leq4\sqrt{2}$。
答案:C
$\because DM,DN,EF$是$\odot A$的切线,$\therefore EM=EP,FN=FP,AM\perp DM,AN\perp DN$。
$\triangle DEF$的周长$l=DE+DF+EF=DE+DF+EP+FP=DE+EM+DF+FN=DM+DN$。
$\because \triangle ABC$是等边三角形,边长为3,$\odot A$半径为1,$\therefore AM=AN=1$。
设$AD=x$,在$Rt\triangle AMD$中,$DM=\sqrt{AD^2 - AM^2}=\sqrt{x^2 - 1}$,同理$DN=\sqrt{x^2 - 1}$,$\therefore l=2\sqrt{x^2 - 1}$。
当D在BC上运动时,AD的最小值为A到BC的距离,即$\frac{\sqrt{3}}{2}×3=\frac{3\sqrt{3}}{2}\approx2.598$,最大值为AB或AC的长3。
$\therefore x_{\text{min}}=\frac{3\sqrt{3}}{2}$,$x_{\text{max}}=3$。
当$x=\frac{3\sqrt{3}}{2}$时,$l=2\sqrt{(\frac{3\sqrt{3}}{2})^2 - 1}=2\sqrt{\frac{27}{4}-1}=2\sqrt{\frac{23}{4}}=\sqrt{23}\approx4.796$;
当$x=3$时,$l=2\sqrt{3^2 - 1}=2\sqrt{8}=4\sqrt{2}\approx5.656$。
$\therefore \sqrt{23}\leq l\leq4\sqrt{2}$。
答案:C
19. 如图,在平面直角坐标系中,O为坐标原点,以点O为圆心作$\odot O$,A,C分别是$\odot O$与x轴负半轴、y轴正半轴的交点,点B,D在$\odot O$上,连接AB,BC,CD,DA,则$∠ADC$的度数是
$135^{\circ}$
.
答案:
【解析】:本题可根据圆内接四边形的性质以及圆周角定理来求解$\angle ADC$的度数。
圆内接四边形的对角互补,即圆内接四边形的任意一组对角之和为$180^{\circ}$。
在圆$O$中,四边形$ABCD$是圆内接四边形,$\angle ABC$与$\angle ADC$是一组对角,所以$\angle ABC + \angle ADC = 180^{\circ}$。
因为$A$,$C$分别是$\odot O$与$x$轴负半轴、$y$轴正半轴的交点,所以$\angle AOC = 90^{\circ}$。
根据圆周角定理:同弧或等弧所对的圆周角等于圆心角的一半。
$\angle ABC$和$\angle AOC$都对着弧$\overset{\frown}{AC}$,所以$\angle ABC=\frac{1}{2}\angle AOC$。
已知$\angle AOC = 90^{\circ}$,则$\angle ABC=\frac{1}{2}×90^{\circ}=45^{\circ}$。
由$\angle ABC + \angle ADC = 180^{\circ}$,$\angle ABC = 45^{\circ}$,可得$\angle ADC = 180^{\circ} - 45^{\circ}=135^{\circ}$。
【答案】:$135^{\circ}$
圆内接四边形的对角互补,即圆内接四边形的任意一组对角之和为$180^{\circ}$。
在圆$O$中,四边形$ABCD$是圆内接四边形,$\angle ABC$与$\angle ADC$是一组对角,所以$\angle ABC + \angle ADC = 180^{\circ}$。
因为$A$,$C$分别是$\odot O$与$x$轴负半轴、$y$轴正半轴的交点,所以$\angle AOC = 90^{\circ}$。
根据圆周角定理:同弧或等弧所对的圆周角等于圆心角的一半。
$\angle ABC$和$\angle AOC$都对着弧$\overset{\frown}{AC}$,所以$\angle ABC=\frac{1}{2}\angle AOC$。
已知$\angle AOC = 90^{\circ}$,则$\angle ABC=\frac{1}{2}×90^{\circ}=45^{\circ}$。
由$\angle ABC + \angle ADC = 180^{\circ}$,$\angle ABC = 45^{\circ}$,可得$\angle ADC = 180^{\circ} - 45^{\circ}=135^{\circ}$。
【答案】:$135^{\circ}$
20. (2023·启东期中)如图,点P,A,B的坐标分别为$(3,4),(2.8,0),(5.6,0),\odot P$的半径为2,M是$\odot P$上的动点,C是线段MB的中点,则AC长的最小值是____
$\frac{3}{2}$
.
答案:
1. 首先,取$OB$的中点$D$:
已知$A(2.8,0)$,$B(5.6,0)$,根据中点坐标公式$x=\frac{x_1 + x_2}{2}$(若有两点$(x_1,y_1)$,$(x_2,y_2)$),对于$O(0,0)$和$B(5.6,0)$,则$D$点坐标为$(\frac{0 + 5.6}{2},0)=(2.8,0)$,所以$A$与$D$重合。
因为$C$是线段$MB$的中点,$A$($D$)是$OB$的中点,根据三角形中位线定理:三角形的中位线平行于第三边且等于第三边的一半,所以$AC=\frac{1}{2}OM$。
2. 然后,求$OM$的最小值:
已知$P(3,4)$,根据两点间距离公式$d=\sqrt{(x_2 - x_1)^2+(y_2 - y_1)^2}$,$O(0,0)$,则$OP=\sqrt{(3 - 0)^2+(4 - 0)^2}=\sqrt{9 + 16}=\sqrt{25}=5$。
因为$M$是$\odot P$上的动点,$\odot P$的半径$r = 2$,根据圆的性质,$OM$的最小值为$OP-r$。
所以$OM_{min}=OP - r$,其中$OP = 5$,$r = 2$,则$OM_{min}=5 - 2=3$。
3. 最后,求$AC$的最小值:
又因为$AC=\frac{1}{2}OM$,所以$AC_{min}=\frac{1}{2}OM_{min}$。
把$OM_{min}=3$代入可得$AC_{min}=\frac{3}{2}$。
故$AC$长的最小值是$\frac{3}{2}$。
已知$A(2.8,0)$,$B(5.6,0)$,根据中点坐标公式$x=\frac{x_1 + x_2}{2}$(若有两点$(x_1,y_1)$,$(x_2,y_2)$),对于$O(0,0)$和$B(5.6,0)$,则$D$点坐标为$(\frac{0 + 5.6}{2},0)=(2.8,0)$,所以$A$与$D$重合。
因为$C$是线段$MB$的中点,$A$($D$)是$OB$的中点,根据三角形中位线定理:三角形的中位线平行于第三边且等于第三边的一半,所以$AC=\frac{1}{2}OM$。
2. 然后,求$OM$的最小值:
已知$P(3,4)$,根据两点间距离公式$d=\sqrt{(x_2 - x_1)^2+(y_2 - y_1)^2}$,$O(0,0)$,则$OP=\sqrt{(3 - 0)^2+(4 - 0)^2}=\sqrt{9 + 16}=\sqrt{25}=5$。
因为$M$是$\odot P$上的动点,$\odot P$的半径$r = 2$,根据圆的性质,$OM$的最小值为$OP-r$。
所以$OM_{min}=OP - r$,其中$OP = 5$,$r = 2$,则$OM_{min}=5 - 2=3$。
3. 最后,求$AC$的最小值:
又因为$AC=\frac{1}{2}OM$,所以$AC_{min}=\frac{1}{2}OM_{min}$。
把$OM_{min}=3$代入可得$AC_{min}=\frac{3}{2}$。
故$AC$长的最小值是$\frac{3}{2}$。
查看更多完整答案,请扫码查看


