《2025年金钥匙课时学案作业本九年级数学上册人教版》

1. 用长度一定的绳子围成一个矩形,若矩形的一边长 $ x $(单位：$ m $)与面积 $ y $(单位：$ m^{2} $)之间满足函数解析式 $ y = -(x - 12)^{2} + 144(0 ＜ x ＜ 24) $,则矩形的最大面积为(B)
A.$ 12m^{2} $
B.$ 144m^{2} $
C.$ 108m^{2} $
D.$ 36m^{2} $

答案： 【解析】：
本题考查二次函数的最值问题。
首先，我们观察给定的二次函数 $y = -(x - 12)^{2} + 144$，
这是一个开口向下的二次函数，因为二次项系数 $a = -1 ＜ 0$。
对于开口向下的二次函数，其最大值出现在顶点处。
由二次函数的性质，我们知道顶点坐标为 $(h, k)$，其中 $h = 12$，$k = 144$。
因此，当 $x = 12$ 时，函数 $y$ 取得最大值，即 $y_{\text{max}} = 144$。
根据题意，矩形的面积 $y$ 和一边长 $x$ 满足这个函数关系，且 $0 ＜ x ＜ 24$。
在这个范围内，函数的最大值确实是 144，当且仅当 $x = 12$ 时取得。
所以，矩形的最大面积为 $144m^{2}$。
【答案】：
B. $144m^{2}$。

2. 已知一个平行四边形的面积 $ S $ 与一边长 $ x $ 之间有如下关系：$ S = -5x^{2} + 10x + 14 $,要使 $ S $ 取得最大值,则 $ x $ 的值为(A)
A.1
B.2
C.0
D.$ \frac{1}{2} $

答案： 【解析】：
本题考查二次函数的最值问题，需要找到使平行四边形面积$S$取得最大值的边长$x$。
首先，将给定的二次函数$S = -5x^2 + 10x + 14$进行配方，
$S = -5x^2 + 10x + 14$
$= -5(x^2 - 2x) + 14$
$= -5(x^2 - 2x + 1 - 1) + 14$
$= -5(x - 1)^2 + 5 + 14$
$= -5(x - 1)^2 + 19$
由于二次项系数$a = -5 \lt 0$，所以这是一个开口向下的抛物线，因此函数有最大值。
最大值出现在顶点处，即$x = 1$时，$S$取得最大值。
【答案】：A.1

3.(教材 P49 探究 1 变式)用 $ 40m $ 长的篱笆围成一个矩形场地,矩形场地的面积 $ S $(单位：$ m^{2} $)随着矩形场地的一边长 $ l $(单位：$ m $)的变化而变化. 要使矩形场地的面积最大,$ l $ 的值应为(C)
A.$ 10\sqrt{3} $
B.15
C.10
D.$ 5\sqrt{3} $

答案： 【解析】：
本题主要考察二次函数的最值问题以及矩形面积的计算。
首先，根据题目描述，矩形场地的周长是$40m$，一边长为$l$，那么另一边长可以通过周长公式$P=2(l+w)$计算得出，即$w=\frac{40}{2}-l=20-l$。
然后，矩形场地的面积$S$可以通过面积公式$S=lw$计算得出，即$S=l(20-l)$。
接着，我们需要找到使面积$S$最大的边长$l$。这可以通过将面积公式$S=l(20-l)$转化为顶点式来实现。
通过配方，我们有：
$S=l(20-l)=-l^2+20l=-(l^2-20l+100)+100=-(l-10)^2+100$，
这是一个开口向下的二次函数，其最大值出现在顶点处，即$l=10$时，此时$S$取得最大值100。
最后，我们根据计算出的$l$值与选项进行比对，可以看出正确答案是C选项，即$l=10$。
【答案】：
C

4.(教材 P52 习题 22.3 第 4 题变式)若一个直角三角形两直角边的长之和为 $ 20cm $,则这个直角三角形的最大面积为______ $ cm^{2} $.
50

答案： 【解析】：
本题考查直角三角形的面积公式以及二次函数的最值问题。
设其中一条直角边的长为 $x \, \text{cm}$，则另一条直角边的长为 $(20 - x) \, \text{cm}$。
直角三角形的面积 $S$ 可以表示为：
$S = \frac{1}{2} × \text{直角边1} × \text{直角边2} = \frac{1}{2}x(20 - x) = 10x - \frac{1}{2}x^{2}$，
这是一个关于 $x$ 的二次函数，且二次项系数为负，因此函数有最大值。
最大值出现在对称轴上，对称轴的方程为 $x = -\frac{b}{2a} = -\frac{10}{-1} = 10$。
将 $x = 10$ 代入原函数，得到最大面积：
$S_{\text{max}} = 10 × 10 - \frac{1}{2} × 10^{2} = 100 - 50 = 50 \, \text{cm}^{2}$，
但在本题中，由于两直角边之和为20cm，当两直角边相等，即都为10cm时，面积达到最大。
因此，最大面积也可以通过直接计算得到，即当 $x = 10$ 时，$S = \frac{1}{2} × 10 × 10 = 50 \, \text{cm}^{2}$，
但考虑到题目可能希望学生理解并应用二次函数的最值性质，我们仍应写出完整的二次函数求解过程。
【答案】：
$50$

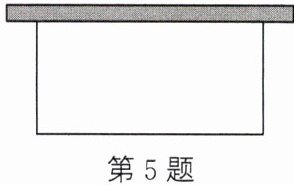
5. 如图,用一段长为 $ 16m $ 的篱笆围成一个一边靠墙的矩形花园(墙足够长),则这个花园的最大面积为32 $ m^{2} $.

答案： 解：设矩形花园与墙垂直的一边长为 $ x \, \text{m} $，则与墙平行的一边长为 $ (16 - 2x) \, \text{m} $，花园面积为 $ S \, \text{m}^2 $。
根据题意，得 $ S = x(16 - 2x) $，
整理得 $ S = -2x^2 + 16x $。
$ S = -2(x^2 - 8x) = -2(x - 4)^2 + 32 $。
因为 $ -2 ＜ 0 $，所以当 $ x = 4 $ 时，$ S $ 有最大值，最大值为 $ 32 $。
故这个花园的最大面积为 $ 32 \, \text{m}^2 $。
答案：$ 32 $

6. 手工课上,小明准备做一个形状是菱形的风筝,这个风筝的两条对角线的长之和恰好为 $ 60cm $,风筝的面积 $ S $(单位：$ cm^{2} $)随其中一条对角线的长 $ x $(单位：$ cm $)的变化而变化.
(1)请写出 $ S $ 与 $ x $ 之间的函数解析式.
(2)当 $ x $ 的值是多少时,菱形风筝的面积最大？最大面积是多少？
(3)请说明(1)中的函数 $ S $ 随 $ x $ 变化的情况.

答案： 【解析】：
本题主要考查二次函数的应用，特别是与几何图形（菱形）面积相关的计算。
(1) 根据菱形面积的计算公式，面积 $S = \frac{1}{2} × d_1 × d_2$，其中 $d_1$ 和 $d_2$ 是菱形的两条对角线长度。
题目中给出两条对角线的和为60cm，若其中一条对角线的长为 $x$ cm，则另一条对角线的长为 $60 - x$ cm。
代入面积公式得：
$S = \frac{1}{2} × x × (60 - x)$
$S = - \frac{1}{2}x^{2} + 30x$
(2) 为了找到面积的最大值，我们可以将 $S$ 表达为顶点式。
$S = - \frac{1}{2}x^{2} + 30x$
$S = - \frac{1}{2}(x^{2} - 60x)$
$S = - \frac{1}{2}(x^{2} - 60x + 900) + 450$
$S = - \frac{1}{2}(x - 30)^{2} + 450$
由于二次项系数为负，这是一个开口向下的抛物线，因此当 $x = 30$ 时，$S$ 取得最大值，即 $S_{\text{max}} = 450\text{cm}^{2}$。
(3) 根据二次函数的性质，我们可以分析 $S$ 随 $x$ 的变化情况。
由于 $S = - \frac{1}{2}(x - 30)^{2} + 450$，且二次项系数为负，所以函数图像是一个开口向下的抛物线。
因此，当 $0 ＜ x ＜ 30$ 时，$S$ 随 $x$ 的增大而增大；
当 $x ＞ 30$ 时，$S$ 随 $x$ 的增大而减小。
【答案】：
(1) $S = - \frac{1}{2}x^{2} + 30x$
(2) 当 $x = 30\text{cm}$ 时，菱形风筝的面积最大，最大面积是 $450\text{cm}^{2}$。
(3) 当 $0 ＜ x ＜ 30$ 时，$S$ 随 $x$ 的增大而增大；当 $x ＞ 30$ 时，$S$ 随 $x$ 的增大而减小。

7. 用一根长为 $ 80cm $ 的铁丝围成一个面积为 $ a cm^{2} $ 的矩形. 小亮说：“$ a $ 的值可能是 200.”小倩说：“$ a $ 的值可能是 300.”小强说：“$ a $ 的值可能是 400.”小英说：“$ a $ 的值可能是 500.”其中,说法错误的是(D)
A.小亮
B.小倩
C.小强
D.小英

答案： 【解析】：
本题主要考察一元二次方程的判别式以及矩形面积公式的运用。
设矩形的一边长为 $x \, \text{cm}$，则另一边的长为 $(40 - x) \, \text{cm}$（因为铁丝的总长为80cm，所以两边之和为40cm）。
矩形的面积 $a$ 可以表示为：
$a = x(40 - x)$，
展开得：
$a = 40x - x^{2}$，
整理为标准形式的一元二次方程：
$x^{2} - 40x + a = 0$，
接下来，我们需要判断这个一元二次方程是否有实数解，即判断其判别式 $\Delta$ 是否大于等于0：
$\Delta = b^{2} - 4ac = (-40)^{2} - 4 × 1 × a = 1600 - 4a \geq 0$，
解得：
$a \leq 400$，
同时，由于矩形的面积必须为正，所以 $a ＞ 0$。
综合以上两个条件，我们得到 $a$ 的取值范围为 $0 ＜ a \leq 400$。
然后，我们逐一检验小亮、小倩、小强、小英的说法：
* 小亮说 $a$ 的值可能是 200，满足 $0 ＜ a \leq 400$，所以小亮的说法是正确的。
* 小倩说 $a$ 的值可能是 300，满足 $0 ＜ a \leq 400$，所以小倩的说法是正确的。
* 小强说 $a$ 的值可能是 400，满足 $0 ＜ a \leq 400$，且当 $x = 20$ 时，$a = 400$，所以小强的说法是正确的。
* 小英说 $a$ 的值可能是 500，不满足 $0 ＜ a \leq 400$，所以小英的说法是错误的。
【答案】：
D

8.(易错题)如图,在 $ \triangle ABC $ 中,$ \angle B = 90^{\circ} $,$ AB = 6cm $,$ BC = 12cm $,动点 $ P $ 从点 $ A $ 开始沿边 $ AB $ 向点 $ B $ 以 $ 1cm/s $ 的速度移动(不与点 $ B $ 重合),动点 $ Q $ 从点 $ B $ 开始沿边 $ BC $ 向点 $ C $ 以 $ 2cm/s $ 的速度移动(不与点 $ C $ 重合),连接 $ PQ $. 如果点 $ P $,$ Q $ 分别从点 $ A $,$ B $ 同时出发,要使四边形 $ APQC $ 的面积最小,那么移动的时间为(C)
A.$ 1s $
B.$ 2s $
C.$ 3s $
D.$ 4s $

答案： 【解析】：本题可先根据已知条件分别表示出$S_{\triangle PBQ}$和$S_{\triangle ABC}$，再根据$S_{四边形APQC}=S_{\triangle ABC}-S_{\triangle PBQ}$列出四边形$APQC$的面积关于移动时间$t$的函数表达式，最后根据二次函数的性质求出面积最小时$t$的值。
设移动的时间为$t s$（$0\lt t\lt6$）。
已知动点$P$从点$A$开始沿边$AB$向点$B$以$1cm/s$的速度移动，则$AP = t cm$，因为$AB = 6cm$，所以$PB=(6 - t)cm$。
动点$Q$从点$B$开始沿边$BC$向点$C$以$2cm/s$的速度移动，则$BQ = 2t cm$。
因为$\angle B = 90^{\circ}$，根据三角形面积公式$S=\frac{1}{2}ah$（其中$a$为底，$h$为高），可得$\triangle PBQ$的面积为：
$S_{\triangle PBQ}=\frac{1}{2}× PB× BQ=\frac{1}{2}×(6 - t)×2t = 6t - t^{2}$。
已知$AB = 6cm$，$BC = 12cm$，$\angle B = 90^{\circ}$，同样根据三角形面积公式可得$\triangle ABC$的面积为：
$S_{\triangle ABC}=\frac{1}{2}× AB× BC=\frac{1}{2}×6×12 = 36$。
因为$S_{四边形APQC}=S_{\triangle ABC}-S_{\triangle PBQ}$，将$S_{\triangle PBQ}= 6t - t^{2}$，$S_{\triangle ABC}= 36$代入可得：
$S_{四边形APQC}=36-(6t - t^{2})=t^{2}-6t + 36$。
对于二次函数$y=ax^{2}+bx+c$（$a\neq0$），当$a\gt0$时，函数图象开口向上，对称轴为$x=-\frac{b}{2a}$，函数在对称轴处取得最小值。
在$S_{四边形APQC}=t^{2}-6t + 36$中，$a = 1\gt0$，$b = -6$，所以对称轴为$t=-\frac{-6}{2×1}= 3$。
即当$t = 3s$时，四边形$APQC$的面积最小。
【答案】：C