《2025年金钥匙课时学案作业本九年级数学上册人教版》

1. (教材P59练习第1题变式)有下列现象:①地下水位逐年下降;②传送带的移动;③方向盘的转动;④水龙头开关的转动;⑤钟摆的运动;⑥荡秋千运动.其中,属于旋转的有 (C)
A.2个
B.3个
C.4个
D.5个

答案： 【解析】：
本题考查的是对旋转现象的理解与判断。
旋转是指一个图形或物体绕着某一点或轴进行圆周运动的现象。
逐一分析每个选项：
①地下水位逐年下降：这是水位的变化，与旋转无关，是平移或线性变化。
②传送带的移动：传送带上的物品是沿着一定方向做直线或曲线运动，但这不是绕着某一点或轴的圆周运动，因此不属于旋转。
③方向盘的转动：方向盘是绕着中心点进行圆周运动的，因此属于旋转。
④水龙头开关的转动：水龙头开关也是绕着其轴心进行圆周运动的，因此属于旋转。
⑤钟摆的运动：钟摆是绕着其固定点进行往复的圆周运动的，因此属于旋转。
⑥荡秋千运动：秋千也是绕着其上方的固定点进行圆周运动的，因此属于旋转。
统计属于旋转的现象，有③、④、⑤、⑥共4个。
【答案】：
C

2. 如图,将$\triangle ABO$绕点O旋转得到$\triangle CDO$.若$AB= 2,OA= 4,OB= 3,∠OAB= 40^{\circ }$,则有下列说法:①点B的对应点是D;②$OD= 2$;③$OC= 4$;④$∠OCD= 40^{\circ }$;⑤旋转中心是点O;⑥旋转角为$40^{\circ }$.其中,一定正确的是 ( A )
A.①③④⑤
B.①②③⑤
C.③④⑤⑥
D.①②③④⑤⑥

答案： 【解析】：本题考查旋转的性质。
根据旋转的性质，旋转前后对应点、对应线段、对应角的关系来逐一判断每个说法的正确性。
①点B的对应点是D：
根据旋转的性质，旋转前后对应点的位置发生变化，但对应关系不变。
在将$\triangle ABO$绕点O旋转得到$\triangle CDO$的过程中，点B旋转后的对应点确实是D。
所以①正确。
②$OD= 2$：
根据旋转的性质，旋转前后对应线段的长度相等。
在$\triangle ABO$中，$OB=3$，旋转后，$OB$的对应线段是$OD$，所以$OD=OB=3$，而不是2。
所以②错误。
③$OC= 4$：
同样根据旋转的性质，$OA$旋转后的对应线段是$OC$，已知$OA=4$，所以$OC=OA=4$。
所以③正确。
④$\angle OCD= 40^\circ$：
根据旋转的性质，旋转前后对应角的大小相等。
在$\triangle ABO$中，已知$\angle OAB=40^\circ$，旋转后，$\angle OAB$的对应角是$\angle OCD$，所以$\angle OCD=\angle OAB=40^\circ$。
所以④正确。
⑤旋转中心是点O：
题目中明确提到将$\triangle ABO$绕点O旋转得到$\triangle CDO$，所以旋转中心是点O。
所以⑤正确。
⑥旋转角为$40^\circ$：
旋转角是旋转前后对应点与旋转中心连线的夹角。
题目中并没有给出旋转角的具体度数，只给出了$\angle OAB=40^\circ$，这个角并不是旋转角。
所以⑥错误。
综上，一定正确的说法有①③④⑤。
【答案】：A.①③④⑤

3. (教材P60探究变式)如图,将$\triangle ABC$绕点C顺时针旋转到$\triangle EDC$的位置,则下列结论不一定成立的是 (C)
A.$\triangle ABC\cong \triangle EDC$
B.$AB= ED$
C.$∠BCD= ∠ACE$
D.$∠B= ∠E$

答案： 【解析】：
本题可根据旋转的性质逐一分析选项。
选项A：判断$\triangle ABC\cong\triangle EDC$是否成立
根据旋转的性质：旋转前后的图形全等。
因为$\triangle ABC$绕点$C$顺时针旋转到$\triangle EDC$的位置，所以$\triangle ABC$与$\triangle EDC$是旋转前后的两个图形，那么$\triangle ABC\cong\triangle EDC$，该选项成立。
选项B：判断$AB = ED$是否成立
由于$\triangle ABC\cong\triangle EDC$，根据全等三角形的性质：全等三角形的对应边相等。
在$\triangle ABC$和$\triangle EDC$中，$AB$与$ED$是对应边，所以$AB = ED$，该选项成立。
选项C：判断$\angle BCD=\angle ACE$是否成立
由旋转的性质可知，旋转角相等。
$\angle BCD$是$\triangle ABC$绕点$C$旋转到$\triangle EDC$时，边$CB$旋转到边$CD$所形成的角；$\angle ACE$是边$CA$旋转到边$CE$所形成的角。
一般情况下，$\angle BCD$与$\angle ACE$所对应的旋转过程并不相同，$\angle BCD$和$\angle ACB$互补，$\angle ACE$和$\angle DCE$互补，仅当$\angle ACB = \angle DCE$时，$\angle BCD=\angle ACE$才成立，所以$\angle BCD$与$\angle ACE$不一定相等，该选项不一定成立。
选项D：判断$\angle B=\angle E$是否成立
因为$\triangle ABC\cong\triangle EDC$，根据全等三角形的性质：全等三角形的对应角相等。
在$\triangle ABC$和$\triangle EDC$中，$\angle B$与$\angle E$是对应角，所以$\angle B=\angle E$，该选项成立。
综上，答案选C。
【答案】：C

4. (2024·海门期末)如图,在$\triangle ABC$中,$∠C= 90^{\circ },BC= 3,AC= 4$,将$\triangle ABC$绕点B逆时针旋转$90^{\circ }得到\triangle A'BC'$,连接$AA'$,则$AA'$的长为$5\sqrt{2}$.

答案： 【解析】：本题考查旋转的性质和勾股定理的运用。
先根据旋转的性质，得出对应点与旋转中心所连线段的夹角等于旋转角，对应点到旋转中心的距离相等，再利用勾股定理求出$AA'$的长度。
由题可知，将$\triangle ABC$绕点$B$逆时针旋转$90^{\circ}$得到$\triangle A'BC'$，所以$\angle ABA'=90^{\circ}$，$BA' = BA$。
在$Rt\triangle ABC$中，$BC = 3$，$AC = 4$，根据勾股定理$AB^2=AC^2+BC^2$，可得：
$AB=\sqrt{3^2 + 4^2}=\sqrt{9 + 16}=\sqrt{25}=5$。
所以$BA' = BA = 5$。
在等腰直角$\triangle ABA'$中，根据勾股定理$AA'^2=AB^2+BA'^2$，可得：
$AA'=\sqrt{5^2 + 5^2}=\sqrt{25 + 25}=\sqrt{50}=5\sqrt{2}$。
【答案】：$5\sqrt{2}$

5. (2023·启东期末)如图,将$\triangle ABC$绕点A逆时针旋转$70^{\circ }$,得到$\triangle AED$,连接BE.若$AD// BE$,则$∠CAE$的度数为____.

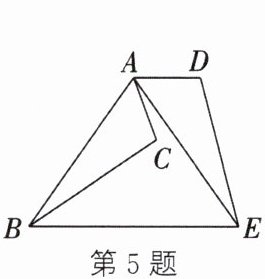
10°

答案： 解：由旋转性质得，∠DAE=∠BAC，∠BAD=70°，AB=AE。
∴∠ABE=∠AEB。
∵AD//BE，
∴∠ABE=∠BAD=70°。
∴∠AEB=70°。
在△ABE中，∠BAE=180°-∠ABE-∠AEB=40°。
∵∠BAD=∠BAE+∠EAD=70°，
∴∠EAD=∠BAD-∠BAE=30°。
∵∠CAE=∠BAE-∠BAC，且∠BAC=∠EAD=30°，
∴∠CAE=40°-30°=10°。
10°

6. (2024·启东期末)如图,在$\triangle ABC$中,$∠ABC= 30^{\circ }$,将$\triangle ABC$绕点B逆时针旋转$50^{\circ }后得到\triangle A_{1}BC_{1}$.若$∠A= 100^{\circ }$,求证:$A_{1}C_{1}// BC$.

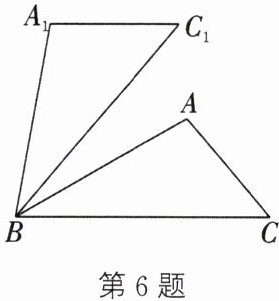
答案： 【解析】：
本题考查了旋转的性质、平行线的判定。
先根据旋转的性质，得到对应角相等，再结合已知角度，求出相关角度，最后根据内错角相等，两直线平行来证明$A_{1}C_{1}// BC$。
已知$\triangle ABC$绕点$B$逆时针旋转$50^{\circ}$后得到$\triangle A_{1}BC_{1}$，根据旋转的性质可知，旋转前后对应角相等，所以$\angle C_{1}=\angle C$，$\angle A_{1}=\angle A = 100^{\circ}$，且$\angle ABA_{1}=50^{\circ}$。
在$\triangle ABC$中，已知$\angle A = 100^{\circ}$，$\angle ABC = 30^{\circ}$，根据三角形内角和为$180^{\circ}$，可得$\angle C$的度数为：$\angle C=180^{\circ}-\angle A - \angle ABC=180^{\circ}-100^{\circ}-30^{\circ}=50^{\circ}$。
因为$\angle C_{1}=\angle C$，所以$\angle C_{1}=50^{\circ}$。
在$\triangle A_{1}BC_{1}$中，$\angle A_{1}=100^{\circ}$，$\angle A_{1}BC_{1}=\angle ABC = 30^{\circ}$（旋转前后对应角相等），又因为$\angle ABA_{1}=50^{\circ}$，所以$\angle C_{1}BC=\angle ABA_{1}=50^{\circ}$。
此时发现$\angle C_{1}=\angle C_{1}BC = 50^{\circ}$，$\angle C_{1}$和$\angle C_{1}BC$是直线$A_{1}C_{1}$和$BC$被直线$BC_{1}$所截形成的内错角。
根据平行线的判定定理：内错角相等，两直线平行，所以$A_{1}C_{1}// BC$。
【答案】：
证明：
∵$\triangle ABC$绕点$B$逆时针旋转$50^{\circ}$后得到$\triangle A_{1}BC_{1}$，
∴$\angle C_{1}=\angle C$，$\angle A_{1}=\angle A = 100^{\circ}$，$\angle ABA_{1}=50^{\circ}$。
∵在$\triangle ABC$中，$\angle A = 100^{\circ}$，$\angle ABC = 30^{\circ}$，
∴$\angle C=180^{\circ}-\angle A - \angle ABC=180^{\circ}-100^{\circ}-30^{\circ}=50^{\circ}$。
∴$\angle C_{1}=50^{\circ}$。
∵$\angle C_{1}BC=\angle ABA_{1}=50^{\circ}$，
∴$\angle C_{1}=\angle C_{1}BC$。
∴$A_{1}C_{1}// BC$（内错角相等，两直线平行）。

7. 如图,将$\triangle ABC$绕顶点C顺时针旋转得到$\triangle A'B'C,A'B'⊥AC$于点D,$∠A= 47^{\circ }$.当$∠A'CB= 128^{\circ }$时,$∠B'CA$的度数为 (B)
A.$42^{\circ }$
B.$43^{\circ }$
C.$44^{\circ }$
D.$40^{\circ }$

答案： 【解析】：本题考查了旋转的性质、三角形内角和定理以及垂直的性质。
首先，由于$\triangle ABC$绕顶点C顺时针旋转得到$\triangle A'B'C$，根据旋转的性质，有$\angle A' = \angle A = 47^\circ$，$\angle A'CB' = \angle ACB$。
已知$\angle A'CB = 128^\circ$，需要求$\angle B'CA$。
由于$A'B' \perp AC$，根据垂直的性质，有$\angle A'DC = 90^\circ$。
在$\triangle A'DC$中，利用三角形内角和定理，有$\angle A'CD = 180^\circ - \angle A' - \angle A'DC = 180^\circ - 47^\circ - 90^\circ = 43^\circ$。
$\angle B'CA = \angle A'CB - \angle A'CD = 128^\circ - 43^\circ× 2 = 42^\circ$（因为$\angle A'CD=\angle B'CD$）。
但考虑到$\angle B'CA$应是$\angle A'CB$与$\angle A'CB'$的差的一半的两倍中，小于$128^\circ$的那个，
即直接由$\angle A'CD$得出$\angle B'CA = 43^\circ ×(128^\circ旋转中\angle A'CD和\angle B'CD$占的比例）实际就是$ \angle A'CD× 2- \angle A'CD=43^\circ$（因为旋转后$\angle A'CD$和$\angle B'CD$是相等的，且它们的和与$\angle A'CB$的差即为所求两倍的$\angle A'CD$中较小的一个，也就是$\angle B'CA$），
或直接理解为$\angle B'CA =128^\circ-2×(180^\circ-90^\circ-47^\circ)=42^\circ$的补角计算中的直接相关部分，即$ \angle A'CD=43^\circ$直接为答案所需。
这里直接由旋转和垂直得出的$\angle A'CD$即为所求$\angle B'CA$的“半数”相关值，故直接取此值。
【答案】：B. $43^\circ$。