《2025年金钥匙课时学案作业本九年级数学上册人教版》

1. (2024·无锡)已知圆锥的底面圆半径为3,母线长为4,则它的侧面积为 (B)
A.$6 \pi$
B.$12 \pi$
C.$15 \pi$
D.$24 \pi$

答案： 【解析】：
本题主要考查圆锥的侧面积公式。
根据圆锥的侧面积公式，侧面积 $S = \pi r l$，其中 $r$ 是底面半径，$l$ 是母线长。
题目给出底面半径 $r = 3$，母线长 $l = 4$。
代入公式得：$S = \pi × 3 × 4 = 12\pi$。
【答案】：B. $12\pi$。

2. 若圆锥底面圆的半径为7 cm,高为24 cm,则它的侧面展开图的面积是 (C)
A.$\frac{175 \pi}{3} \mathrm{cm}^2$
B.$\frac{175 \pi}{2} \mathrm{cm}^2$
C.$175 \pi \mathrm{cm}^2$
D.$350 \pi \mathrm{cm}^2$

答案： 解：圆锥底面圆的半径 $ r = 7 \, \text{cm} $，高 $ h = 24 \, \text{cm} $。
圆锥的母线长 $ l = \sqrt{r^2 + h^2} = \sqrt{7^2 + 24^2} = \sqrt{49 + 576} = \sqrt{625} = 25 \, \text{cm} $。
侧面展开图的面积 $ S_{\text{侧}} = \pi r l = \pi × 7 × 25 = 175\pi \, \text{cm}^2 $。
答案：C

3. (教材P114练习第1题变式)(2024·通州期中)某校九年级学生参加社团活动,学习编织圆锥形工艺品. 若这种圆锥的母线长为90 cm,底面圆的直径为80 cm,则该圆锥的全面积为 (B)
A.$3600 \pi \mathrm{cm}^2$
B.$5200 \pi \mathrm{cm}^2$
C.$7200 \pi \mathrm{cm}^2$
D.$8800 \pi \mathrm{cm}^2$

答案： 【解析】：
本题考查圆锥的全面积计算，需要用到圆锥的底面积和侧面积公式。
圆锥的底面是一个圆，其面积公式为$\pi r^2$，其中r为底面半径。
圆锥的侧面展开后是一个扇形，其面积公式为$\pi rl$，其中r为底面半径，l为母线长。
根据题意，圆锥的母线长为90 cm，底面圆的直径为80 cm，所以底面半径$r = \frac{80}{2} = 40$ cm。
代入公式计算底面积：$\pi × 40^2 = 1600\pi \mathrm{cm}^2$。
代入公式计算侧面积：$\pi × 40 × 90 = 3600\pi \mathrm{cm}^2$。
圆锥的全面积 = 底面积 + 侧面积 = $1600\pi + 3600\pi = 5200\pi \mathrm{cm}^2$。
【答案】：
B. $5200 \pi \mathrm{cm}^2$。

4. (2024·扬州)若用半径为10 cm的半圆形纸片围成一个圆锥,则这个圆锥的底面圆的半径为5cm.

答案： 【解析】：
本题主要考查圆锥的侧面展开图与全面积的关系。
首先，计算半圆的弧长。
给定半圆的半径为$10cm$，因此半圆的弧长 $L$ 为：
$L = \frac{1}{2} × 2\pi × 10 = 10\pi \text{(cm)}$，
这也是圆锥底面的周长。
设圆锥底面圆的半径为 $r$ cm。
根据圆的周长公式，有：
$2\pi r = 10\pi$，
解这个方程，得到：
$r = 5 \text{(cm)}$，
所以，这个圆锥的底面圆的半径为 $5cm$。
【答案】：
5

5. 已知圆锥的底面圆的半径为3,侧面积为$12 \pi$,则这个圆锥的母线长为4.

答案： 【解析】：
本题主要考查圆锥的侧面积公式。
根据圆锥的侧面积公式：
$S_{侧} = \pi r l$
其中，$r$ 是底面半径，$l$ 是母线长。
题目给出 $S_{侧} = 12\pi$ 和 $r = 3$，代入公式得：
$12\pi = \pi × 3 × l$
化简得：
$l = \frac{12\pi}{3\pi} = 4$
所以，这个圆锥的母线长为4。
【答案】：
4

6. (2024·齐齐哈尔)若圆锥的底面圆的半径是1 cm,它的侧面展开图的圆心角是直角,则该圆锥的高为$\sqrt{15}$cm.

答案： 【解析】：
本题主要考查圆锥的侧面展开图及全面积的相关知识点。
首先，知道圆锥的底面圆的半径是$1 \text{cm}$，所以底面圆的周长为 $2\pi × 1 = 2\pi \text{cm}$。
又因为圆锥侧面展开图的圆心角是直角，即圆心角为 $90^\circ$ 或 $\frac{\pi}{2}$ 弧度，设圆锥的母线长为 $R$，则根据弧长公式，侧面展开图的弧长等于底面的周长，即：
$\frac{\pi}{2} × R = 2\pi \implies R = 4 \text{cm}$，
现在，有了圆锥的底面半径 $r = 1 \text{cm}$ 和母线长 $R = 4 \text{cm}$，可以利用勾股定理求出圆锥的高 $h$：
$h = \sqrt{R^2 - r^2} = \sqrt{4^2 - 1^2} = \sqrt{16 - 1} = \sqrt{15} \text{cm}$。
【答案】：
$\sqrt{15}$

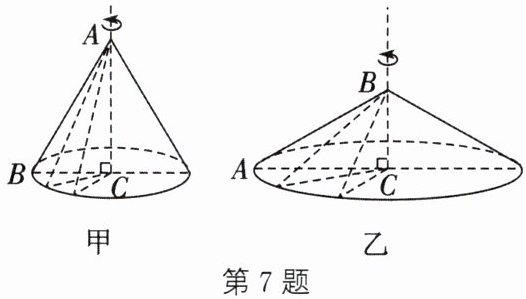
7. (新视角·操作实践题)在数学实验课上,小莹将含$30^{\circ}$角的三角尺分别以两条直角边所在直线为轴旋转一周,得到甲、乙两个圆锥,并用作图软件画出如图所示的示意图. 小亮观察后说：“甲、乙两个圆锥的侧面都是由三角尺的斜边AB旋转得到的,所以它们的侧面积相等.”小亮的说法正确吗? 请说明理由.
]

答案： 【解析】：本题主要考查圆锥的侧面积公式。
圆锥的侧面积公式为：$S=\pi rl$，其中r是底面半径，l是母线长。
对于甲圆锥，底面半径$r_{1}$是$30^{\circ}$角所对的直角边，
根据三角函数，$r_{1}=BC=\frac{\sqrt{3}}{3} AC$，
母线长$l_{1}=AB$。
所以，甲圆锥的侧面积$S_{1}=\pi× \frac{\sqrt{3}}{3} AC× AB$。
对于乙圆锥，底面半径$r_{2}$是另一条直角边AC，
母线长$l_{2}=AB$。
所以，乙圆锥的侧面积$S_{2}=\pi× AC× AB$。
由于$\frac{\sqrt{3}}{3} \ne1$，所以$S_{1}\ne S_{2}$。
因此，小亮的说法不正确。
【答案】：小亮的说法不正确，理由见上述解析。

8. (2024·海门期末)若一个圆锥的侧面积是底面积的2倍,则该圆锥侧面展开图的圆心角的度数为 (B)
A.$120^{\circ}$
B.$180^{\circ}$
C.$240^{\circ}$
D.$300^{\circ}$

答案： 【解析】：
本题主要考查圆锥的侧面积和底面积的关系以及圆锥侧面展开图的性质。
设圆锥的底面半径为$r$，母线长为$l$。
圆锥的底面积为$\pi r^{2}$，侧面积为$\pi rl$。
根据题意，侧面积是底面积的2倍，即：
$\pi rl = 2\pi r^{2}$，
化简得：
$l = 2r$，
圆锥侧面展开图是一个扇形，其弧长等于圆锥底面的周长，即$2\pi r$，半径等于圆锥的母线长$l$。
设圆锥侧面展开图的圆心角为$n^{\circ}$，则根据扇形的性质有：
$\frac{n\pi × l}{180} = 2\pi r$，
将$l = 2r$代入上式得：
$\frac{n\pi × 2r}{180} = 2\pi r$，
化简得：
$n = 180$，
所以，圆锥侧面展开图的圆心角的度数为$180^{\circ}$。
【答案】：B. $180^{\circ}$。

9. (2023·赤峰)某班学生表演课本剧,要制作一顶圆锥形的小丑帽. 如图,这个圆锥的底面圆周长为$20 \pi \mathrm{cm}$,母线AB长为30 cm,为了使帽子更美观,要粘贴彩带进行装饰,其中需要粘贴一条从点A处开始,绕侧面一周又回到点A的彩带(彩带宽度忽略不计),则这条彩带的长最小为 ( B )
A.30 cm
B.$30 \sqrt{3} \mathrm{cm}$
C.60 cm
D.$20 \pi \mathrm{cm}$
]

答案： 【解析】：本题可先根据圆锥底面圆周长求出底面圆半径，再求出圆锥侧面展开图扇形的圆心角，最后根据弧长公式求出彩带的最短长度。
步骤一：求圆锥底面圆半径$r$。
已知圆锥底面圆周长为$20\pi\mathrm{cm}$，根据圆的周长公式$C = 2\pi r$（其中$C$为周长，$r$为半径），可得$2\pi r = 20\pi$，两边同时除以$2\pi$，解得$r = 10\mathrm{cm}$。
步骤二：求圆锥侧面展开图扇形的圆心角$n$。
设圆锥侧面展开图扇形的圆心角为$n^{\circ}$，圆锥底面圆周长等于侧面展开图扇形的弧长。
已知母线$AB$长为$30\mathrm{cm}$，即侧面展开图扇形的半径$R = 30\mathrm{cm}$，根据弧长公式$l=\frac{n\pi R}{180}$（其中$l$为弧长，$n$为圆心角度数，$R$为半径），可得$\frac{n\pi×30}{180}=20\pi$，两边同时乘以$180$再除以$30\pi$，解得$n = 120^{\circ}$。
步骤三：求彩带的最短长度。
将圆锥侧面展开，彩带的最短长度为展开图扇形中弦$AA'$的长度。
连接$AA'$，过圆心$O$作$OD\perp AA'$于点$D$，则$AD = \frac{1}{2}AA'$，$\angle AOD = \frac{1}{2}\angle AOA' = \frac{1}{2}×120^{\circ} = 60^{\circ}$。
在$Rt\triangle AOD$中，$OA = 30\mathrm{cm}$，$\sin\angle AOD = \frac{AD}{OA}$，即$\sin60^{\circ} = \frac{AD}{30}$，$\sin60^{\circ}=\frac{\sqrt{3}}{2}$，所以$AD = 30×\sin60^{\circ} = 30×\frac{\sqrt{3}}{2} = 15\sqrt{3}\mathrm{cm}$，则$AA' = 2AD = 2×15\sqrt{3} = 30\sqrt{3}\mathrm{cm}$。
【答案】：B