《2025年金钥匙课时学案作业本九年级数学上册人教版》

1. (教材 P69 练习第 2 题变式)(2023·海门期末)在平面直角坐标系中,与点 $ P(-1,5) $ 关于原点对称的点的坐标是 (C)
A.$ (5,-1) $
B.$ (1,5) $
C.$ (1,-5) $
D.$ (-5,-1) $

答案： 【解析】：
本题考查平面直角坐标系中关于原点对称的点的坐标性质。在平面直角坐标系中，任意一点$P(x,y)$关于原点的对称点为$P'(-x,-y)$，即坐标符号相反。这是解决本题的关键知识点。
对于点$P(-1,5)$，其横坐标为-1，纵坐标为5。
根据关于原点对称的点的坐标性质，点$P$关于原点的对称点的横坐标应为-(-1)=1，纵坐标应为-
(5)=-5。
所以，与点$P(-1,5)$关于原点对称的点的坐标是$(1,-5)$。
【答案】：
C. $(1,-5)$。

2. 在平面直角坐标系中,把点 $ P(4,3) $ 绕着原点旋转 $ 180^{\circ} $ 后得到点 $ Q $,则点 $ Q $ 的坐标是 (C)
A.$ (4,-3) $
B.$ (-3,-4) $
C.$ (-4,-3) $
D.$ (-4,3) $

答案： 【解析】：
本题考查的是平面直角坐标系中关于原点对称的点的坐标变化规律。
在平面直角坐标系中，任意一点$P(x, y)$绕着原点旋转$180^{\circ}$后，其对称点的坐标变为$(-x, -y)$。
这是因为旋转$180^{\circ}$相当于进行了一次中心对称变换，即关于原点对称。
对于点$P(4, 3)$，其关于原点的对称点$Q$的坐标应为$(-4, -3)$。
【答案】：
C. $(-4, -3)$。

3. 若点 $ P(x,3) $ 与点 $ Q(4,y) $ 关于原点对称,则 $ xy $ 的值是 (A)
A.$ 12 $
B.$ -12 $
C.$ 64 $
D.$ -64 $

答案： 解：
∵点P(x,3)与点Q(4,y)关于原点对称，
∴x=-4，y=-3，
∴xy=(-4)×(-3)=12。
答案：A

4. (2024·通州期末)在平面直角坐标系中,点 $ (1,-4) $ 关于原点对称的点的坐标是$(-1, 4)$.

答案： 【解析】：
本题考查的是平面直角坐标系中关于原点对称的点的坐标性质。在平面直角坐标系中，任意一点$P(x, y)$关于原点的对称点$P'$的坐标是$(-x, -y)$。
根据这一性质，我们可以直接求出点$(1, -4)$关于原点的对称点。
【答案】：
点$(1, -4)$关于原点的对称点的坐标是$(-1, 4)$。

5. (2024·海安期中)若点 $ A(1,a) $ 与点 $ B(-1,-2) $ 关于原点对称,则 $ a $ 的值为2.

答案： 【解析】：
题目考查了关于原点对称的点的坐标性质。在平面直角坐标系中，如果两点关于原点对称，则它们的横、纵坐标都是互为相反数。即，如果点$A(x_1, y_1)$与点$B(x_2, y_2)$关于原点对称，那么有$x_1 = -x_2$和$y_1 = -y_2$。
根据题意，点$A(1,a)$与点$B(-1,-2)$关于原点对称，因此可以应用上述性质，得到$a = -(-2) = 2$。
【答案】：
$a = 2$。

6. (2023·海门期中)在平面直角坐标系中,若点 $ A(m - 1,-3),B(2,n) $ 关于原点对称,则 $ m + n = $____2.

答案： 【解析】：
本题主要考查平面直角坐标系中关于原点对称的点的坐标性质。
根据关于原点对称的点的坐标性质，如果两点关于原点对称，则它们的横、纵坐标互为相反数。
设点$A(m - 1, -3)$和点$B(2, n)$关于原点对称，则有：
$m - 1 = -2$ （因为点B的横坐标是2，所以点A的横坐标$m-1$应为-2）。
$-3 = -n$ （因为点B的纵坐标是$n$，所以点A的纵坐标-3应与$n$互为相反数）。
解这两个方程，得到：
$m - 1 = -2 \Rightarrow m = -1$。
$-3 = -n \Rightarrow n = 3$。
最后求$m + n = -1 + 3 = 2$。
【答案】：
$2$。

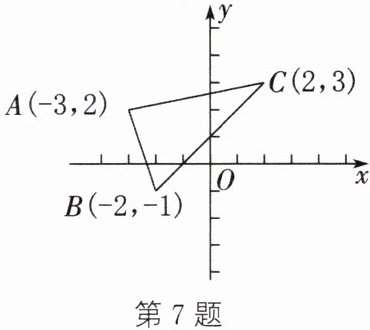
7. (教材 P68 例 2 变式)如图,$ \triangle ABC $ 三个顶点的坐标分别为 $ A(-3,2),B(-2,-1),C(2,3) $,利用关于原点对称的点的坐标的特点,作出 $ \triangle ABC $ 关于原点对称的 $ \triangle A'B'C' $ (简要说明,其中点 $ A,B,C $ 的对应点分别为 $ A',B',C' $ ).
]

答案：
【解析】：
本题考查关于原点对称的点的坐标变化规律。
在平面直角坐标系中，关于原点对称的点的坐标特征是横、纵坐标都互为相反数。
即点$P(x,y)$关于原点对称的点$P'$的坐标为$(-x,-y)$。
已知$\triangle ABC$三个顶点的坐标分别为$A(-3,2)$，$B(-2,-1)$，$C(2,3)$，根据上述规律求出$A'$、$B'$、$C'$的坐标，然后在平面直角坐标系中描出这些点，最后依次连接即可得到$\triangle A'B'C'$。
对于点$A(-3,2)$，关于原点对称的点$A'$的横坐标为$-(-3)=3$，纵坐标为$-2$，所以$A'$的坐标为$(3,-2)$。
对于点$B(-2,-1)$，关于原点对称的点$B'$的横坐标为$-(-2)=2$，纵坐标为$-(-1)=1$，所以$B'$的坐标为$(2,1)$。
对于点$C(2,3)$，关于原点对称的点$C'$的横坐标为$-2$，纵坐标为$-3$，所以$C'$的坐标为$(-2,-3)$。
在平面直角坐标系中分别描出$A'(3,-2)$、$B'(2,1)$、$C'(-2,-3)$这三个点，然后依次连接$A'B'$、$B'C'$、$C'A'$，就得到了$\triangle A'B'C'$。
【答案】：
$A'(3,-2)$，$B'(2,1)$，$C'(-2,-3)$，

8. 在平面直角坐标系中,点 $ P(-3,m^{2}+4m + 5) $ 关于原点对称的点在 (D)
A.第一象限
B.第二象限
C.第三象限
D.第四象限

答案： 【解析】：
本题主要考察平面直角坐标系中关于原点对称的点的坐标性质以及二次函数的性质。
首先，我们需要确定点$P$的纵坐标$m^{2} + 4m + 5$的符号。
考虑二次函数$y = m^{2} + 4m + 5$，可以重写为$y = (m + 2)^{2} + 1$。
由于$(m + 2)^{2} \geq 0$，所以$(m + 2)^{2} + 1 ＞ 0$。
因此，点$P$的纵坐标总是正的。
又因为点$P$的横坐标为$-3$（负的），所以点$P$位于第二象限。
接下来，考虑点$P$关于原点对称的点。
根据对称性质，如果点$P(x, y)$关于原点对称，则其对称点的坐标为$(-x, -y)$。
因此，点$P(-3, m^{2} + 4m + 5)$关于原点对称的点的坐标为$(3, -(m^{2} + 4m + 5))$。
由于这个对称点的横坐标为正，纵坐标为负，所以它位于第四象限。
【答案】：
D. 第四象限。

9. 已知点 $ P(-1 - 2a,2a - 4) $ 关于原点对称的点在第一象限内,则整数 $ a $ 的值可以为 (C)
A.$ 1 $
B.$ 0 $
C.$ 0,1 $
D.$ 0,1,2 $

答案： 【解析】：
本题主要考查了关于原点对称的点的坐标性质以及一元一次不等式组的解法。
首先，点$P(-1 - 2a, 2a - 4)$关于原点对称的点在第一象限内，根据关于原点对称的点的坐标性质，如果点$P(x, y)$关于原点对称的点在第一象限，那么点$P$必须在第三象限。
因此，我们有以下不等式组：
$\begin{cases}-1 - 2a ＜ 0, \\2a - 4 ＜ 0.\end{cases}$
解这个不等式组，我们得到：
$\begin{cases}-2a ＜ 1, \\2a ＜ 4.\end{cases}$
进一步解得：
$\begin{cases}a ＞ -\frac{1}{2}, \\a ＜ 2.\end{cases}$
综合这两个不等式，我们得到$a$的取值范围为$-\frac{1}{2} ＜ a ＜ 2$。
然后，根据题目要求$a$为整数，所以$a$只能取$0$或$1$。
【答案】：
C. $0,1$

10. (易错题)在平面直角坐标系中,点 $ A $ 的坐标为 $ (3,2) $,作点 $ A $ 关于 $ y $ 轴的对称点 $ A_{1} $,作点 $ A_{1} $ 关于原点的对称点 $ A_{2} $,作点 $ A_{2} $ 关于 $ x $ 轴的对称点 $ A_{3} $,作点 $ A_{3} $ 关于 $ y $ 轴的对称点 $ A_{4} $,作点 $ A_{4} $ 关于原点的对称点 $ A_{5} … … $ 按此规律,则点 $ A_{2023} $ 的坐标为____(-3,2).

答案： 1. 首先求$A_1$的坐标：
关于$y$轴对称的点纵坐标不变，横坐标互为相反数。
已知$A(3,2)$，则$A_1(-3,2)$。
2. 然后求$A_2$的坐标：
关于原点对称的点横、纵坐标都互为相反数。
因为$A_1(-3,2)$，所以$A_2(3,-2)$。
3. 接着求$A_3$的坐标：
关于$x$轴对称的点横坐标不变，纵坐标互为相反数。
由于$A_2(3,-2)$，则$A_3(3,2)$。
4. 再求$A_4$的坐标：
关于$y$轴对称的点纵坐标不变，横坐标互为相反数。
因为$A_3(3,2)$，所以$A_4(-3,2)$。
5. 观察规律：
可以发现每$3$次变换为一个循环。
$2023÷3 = 674\cdots\cdots1$，其中$1$是余数。
这说明$A_{2023}$的坐标与$A_1$的坐标相同。
所以点$A_{2023}$的坐标为$(-3,2)$。

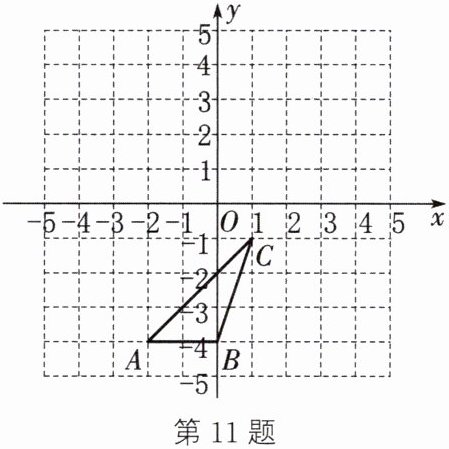
11. 如图,在平面直角坐标系中,$ \triangle ABC $ 的顶点均在格点上,点 $ A $ 的坐标为 $ (-2,-4) $,点 $ B $ 的坐标为 $ (0,-4) $,点 $ C $ 的坐标为 $ (1,-1) $.
(1) 请画出 $ \triangle ABC $ 关于原点 $ O $ 成中心对称的 $ \triangle A_{1}B_{1}C_{1} $ (点 $ A,B,C $ 的对应点分别为 $ A_{1},B_{1},C_{1} $ );
(2) 请画出将 $ \triangle ABC $ 绕原点 $ O $ 逆时针旋转 $ 90^{\circ} $ 后得到的 $ \triangle A_{2}B_{2}C_{2} $ (点 $ A,B,C $ 的对应点分别为 $ A_{2},B_{2},C_{2} $ );
(3) 求 $ \triangle AA_{1}A_{2} $ 的面积.
]

答案：
 
3. （3）
解：
已知$A(-2,-4)$，$A_1(2,4)$，$A_2(4,-2)$。
我们可以利用割补法求$\triangle AA_1A_2$的面积。
以$(4,4)$，$(4, - 4)$，$(-2,4)$，$(-2,-4)$为顶点的矩形面积$S=(4 + 2)×(4 + 4)=48$。
三个直角三角形的面积：
以$(-2,-4)$，$(2,-4)$，$(2,4)$为顶点的直角三角形面积$S_1=\frac{1}{2}×(2 + 2)×(4 + 4)=16$；
以$(2,4)$，$(4,4)$，$(4,-2)$为顶点的直角三角形面积$S_2=\frac{1}{2}×(4 - 2)×(4+2)=6$；
以$(-2,-4)$，$(-2,4)$，$(4,-4)$为顶点的直角三角形面积$S_3=\frac{1}{2}×(4 + 2)×(4 + 2)=18$。
根据$S_{\triangle AA_1A_2}=S - S_1 - S_2 - S_3$。
则$S_{\triangle AA_1A_2}=48-16 - 6-18$
$S_{\triangle AA_1A_2}=8$。
所以$\triangle AA_1A_2$的面积为$8$。