《2025年金钥匙课时学案作业本九年级数学上册人教版》

8. (2023·海门期中)如图,在$□ ABCD$中,$∠A= 70^{\circ }$,将$□ ABCD$绕顶点B顺时针旋转得到$□ A_{1}BC_{1}D_{1}$.当$C_{1}D_{1}$首次经过顶点C时,旋转角的度数是 (B)
A.$30^{\circ }$
B.$40^{\circ }$
C.$45^{\circ }$
D.$50^{\circ }$

答案： 【解析】：本题可根据平行四边形的性质以及旋转的性质来求解旋转角的度数。
步骤一：分析平行四边形的性质
已知四边形$ABCD$是平行四边形，根据平行四边形的性质：平行四边形的邻角互补，可得$\angle A + \angle ABC = 180^{\circ}$。
因为$\angle A = 70^{\circ}$，所以$\angle ABC = 180^{\circ} - 70^{\circ} = 110^{\circ}$。
步骤二：分析旋转后图形的性质
将$□ ABCD$绕顶点$B$顺时针旋转得到$□ A_{1}BC_{1}D_{1}$，当$C_{1}D_{1}$首次经过顶点$C$时，$BC = BC_{1}$，所以$\triangle BCC_{1}$是等腰三角形。
根据旋转的性质可知$\angle CBC_{1}$就是旋转角，且$\angle BCC_{1} = \angle C_{1}$。
步骤三：求旋转角的度数
在$\triangle BCC_{1}$中，$\angle ABC_{1} = \angle ABC - \angle C_{1}BC_{1}=110^{\circ}-\angle C_{1}BC_{1}$，根据三角形内角和为$180^{\circ}$，可得$\angle CBC_{1}+ \angle BCC_{1} + \angle C_{1}=180^{\circ}$。
因为$\angle BCC_{1} = \angle C_{1}$，所以$\angle CBC_{1}=180^{\circ}-2\angle BCC_{1}=180^{\circ}-2\angle C_{1}$，又因为$\angle ABC_{1} + \angle C_{1}BC_{1}= \angle ABC = 110^{\circ}$，即$\angle ABC_{1} + \angle CBC_{1}= 110^{\circ}$，将$\angle ABC_{1} = 110^{\circ}-\angle C_{1}BC_{1}$代入可得：
$110^{\circ}-\angle C_{1}BC_{1}+\angle CBC_{1}= 110^{\circ}$，即$\angle CBC_{1}=180^{\circ}-2×(110^{\circ}-\angle CBC_{1})$
$ \angle CBC_{1}=180^{\circ}-220^{\circ}+2\angle CBC_{1}$
$\angle CBC_{1}= 40^{\circ}$
即旋转角的度数是$40^{\circ}$。
【答案】：B

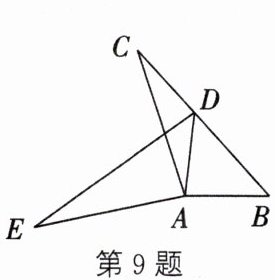
9. (2023·海安期末)如图,在$\triangle ABC$中,$∠BAC= 108^{\circ }$,将$\triangle ABC$绕点A逆时针旋转得到$\triangle ADE$.若点D恰好落在边BC上,且$AD= CD$,则$∠E$的度数是____24°.

答案： 解：设∠C = x。
∵AD = CD，
∴∠CAD = ∠C = x。
∵∠BAC = 108°，
∴∠BAD = ∠BAC - ∠CAD = 108° - x。
∵△ABC绕点A逆时针旋转得到△ADE，
∴AD = AB，∠E = ∠C = x。
∴∠ADB = ∠B。
在△ABD中，∠ADB = ∠B = [180° - ∠BAD]/2 = [180° - (108° - x)]/2 = (72° + x)/2。
在△ADC中，∠ADC = 180° - ∠CAD - ∠C = 180° - 2x。
∵∠ADB + ∠ADC = 180°，
∴(72° + x)/2 + 180° - 2x = 180°。
解得x = 24°。
∴∠E = 24°。
答案：24°

10. (易错题)在如图所示的方格纸中,每个小正方形的边长均为1个单位长度,$\triangle ABC$的顶点都在格点上.将$\triangle ABC$绕点O顺时针旋转得到$\triangle A'B'C'$,使各顶点仍在格点上,则其旋转角的度数是$90^{\circ}$.

答案： 【解析】：本题主要考查旋转的性质以及旋转角的确定。
在平面内，将一个图形绕一点按某个方向转动一个角度，这样的运动叫做图形的旋转。这个定点叫做旋转中心，转动的角度叫做旋转角。
观察图形可知，$\triangle ABC$绕点$O$顺时针旋转后得到$\triangle A'B'C'$，且顶点仍在格点上。
连接$OB$，$OB'$，则$\angle BOB'$就是旋转角。
通过观察方格纸，我们可以发现，$OB$和$OB'$之间的格数关系可以确定旋转的角度。
由于每个小正方形的边长均为1，通过计算或观察，我们可以得到$\angle BOB' = 90^{\circ}$。
【答案】：$90^{\circ}$

11. 如图①,$\triangle ABC$是等边三角形,点D在$\triangle ABC$的内部,连接AD,将线段AD绕点A逆时针旋转$60^{\circ }$,得到线段AE,连接BD,DE,CE.
(1) 判断线段BD,CE之间的数量关系,并证明.
(2) 延长ED交直线BC于点F.如图②,当点F与点B重合时,用等式表示线段AE,BE,CE之间的数量关系,并证明.

答案： 【解析】：本题主要考查等边三角形的性质、旋转的性质以及全等三角形的判定与性质。
（1）判断线段$BD$，$CE$之间的数量关系：
判断：$BD = CE$。
证明：
因为$\triangle ABC$是等边三角形，所以$AB = AC$，$\angle BAC = 60^{\circ}$。
由旋转的性质可知$AD = AE$，$\angle DAE = 60^{\circ}$。
因为$\angle BAC = \angle BAD + \angle DAC = 60^{\circ}$，$\angle DAE = \angle EAC + \angle DAC = 60^{\circ}$，所以$\angle BAD = \angle EAC$。
在$\triangle ABD$和$\triangle ACE$中：
$\begin{cases}AB = AC,\\\angle BAD = \angle EAC,\\AD = AE.\end{cases}$
根据全等三角形判定定理（$SAS$）可得$\triangle ABD\cong\triangle ACE$。
根据全等三角形的性质，全等三角形的对应边相等，所以$BD = CE$。
（2）当点$F$与点$B$重合时，用等式表示线段$AE$，$BE$，$CE$之间的数量关系：
数量关系：$BE = AE + CE$。
证明：
因为$\triangle ABC$是等边三角形，所以$AB = BC = AC$，$\angle BAC = \angle ABC = 60^{\circ}$。
由（1）可知$\triangle ABD\cong\triangle ACE$，所以$BD = CE$，$\angle ABD = \angle ACE$。
因为线段$AD$绕点$A$逆时针旋转$60^{\circ}$得到线段$AE$，所以$\triangle ADE$是等边三角形，那么$\angle ADE = 60^{\circ}$。
因为点$F$与点$B$重合，所以$\angle BDF = \angle ADE = 60^{\circ}$，又因为$\angle ABC = 60^{\circ}$，在$\triangle BDF$中，$\angle BFD = 180^{\circ} - \angle BDF - \angle ABC = 180^{\circ} - 60^{\circ} - 60^{\circ} = 60^{\circ}$，所以$\triangle BDF$是等边三角形，则$BD = BF = DF$。
因为$AB = BC$，$BD = CE$，所以$BE = BC + CE = AB + BD$。
又因为$BD = DF = AE$（$\triangle ADE$是等边三角形，$AD = AE$，且$AD = BD$），所以$BE = AE + CE$。
【答案】：（1）$BD = CE$，证明见上述过程；
（2）$BE = AE + CE$，证明见上述过程。

12. (新视角·探究题)$\triangle ABC和\triangle ADE$都是等边三角形.当$\triangle ADE$绕点A旋转到如图①所示的位置时,连接BD,CE相交于点P,连接PA.
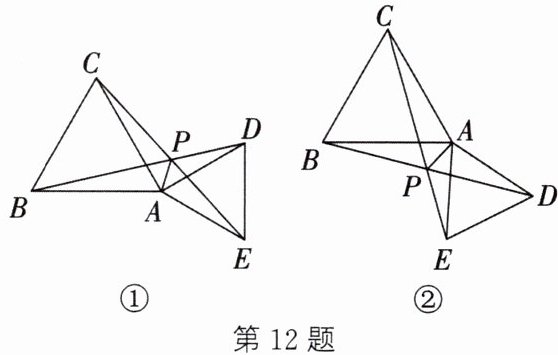
(1) 请猜想线段PA,PB,PC之间的数量关系,并加以证明;
(2) 将$\triangle ADE$绕点A旋转到如图②所示的位置,其他条件不变,请直接写出线段PA,PB,PC之间的数量关系,不需要证明.

答案： 1. （1）
猜想：$PB = PC + PA$。
证明：
因为$\triangle ABC$和$\triangle ADE$都是等边三角形，所以$AB = AC$，$AD = AE$，$\angle BAC=\angle DAE = 60^{\circ}$。
则$\angle BAC+\angle CAD=\angle DAE+\angle CAD$，即$\angle BAD=\angle CAE$。
在$\triangle BAD$和$\triangle CAE$中，$\begin{cases}AB = AC\\\angle BAD=\angle CAE\\AD = AE\end{cases}$，根据$SAS$（边角边）定理可得$\triangle BAD\cong\triangle CAE$。
所以$\angle ABD=\angle ACE$。
在$PB$上截取$PF = PC$，连接$CF$。
因为$\angle BPC=\angle BAC = 60^{\circ}$（由$\angle ABD=\angle ACE$，根据三角形内角和定理可得），所以$\triangle PCF$是等边三角形（有一个角是$60^{\circ}$的等腰三角形是等边三角形，$PF = PC$，$\angle BPC = 60^{\circ}$）。
则$PC = CF$，$\angle PCF = 60^{\circ}$。
又因为$\angle ACB=\angle PCF = 60^{\circ}$，所以$\angle ACB-\angle ACF=\angle PCF-\angle ACF$，即$\angle BCF=\angle ACP$。
且$BC = AC$，$CF = PC$，在$\triangle BCF$和$\triangle ACP$中，$\begin{cases}BC = AC\\\angle BCF=\angle ACP\\CF = PC\end{cases}$，根据$SAS$定理可得$\triangle BCF\cong\triangle ACP$。
所以$BF = PA$。
因为$PB=BF + PF$，$PF = PC$，$BF = PA$，所以$PB = PC + PA$。
2. （2）
数量关系：$PC = PB+PA$。
综上，（1）$PB = PC + PA$；（2）$PC = PB + PA$。