《2025年金钥匙课时学案作业本九年级数学上册人教版》

8. (分类讨论思想)已知一元二次方程$(x-3)^{2}= 1$的两个根恰好分别是等腰三角形ABC的底边长和腰长,则等腰三角形ABC的周长为(A)
A.10
B.10或8
C.9
D.8

答案： 【解析】：
本题主要考查一元二次方程的解法和等腰三角形的性质。首先，我们需要解出一元二次方程$(x-3)^{2}= 1$的两个根，然后根据等腰三角形的性质，分别讨论这两个根作为等腰三角形的底边长和腰长的情况，最后计算出等腰三角形的周长。
1. 解一元二次方程$(x-3)^{2}= 1$：
对方程两边同时开平方，得到$x-3 = \pm 1$。
解得$x_1 = 4$，$x_2 = 2$。
2. 讨论等腰三角形的底边长和腰长：
当腰长为2，底边长为4时：由于$2 + 2 = 4$，不满足三角形的三边关系（任意两边之和大于第三边），所以这种情况不成立。
当腰长为4，底边长为2时：满足三角形的三边关系，因此周长为$4 + 4 + 2 = 10$。
【答案】：
A. 10。

9. (易错题)若方程$(ax-1)^{2}-16= 0的一个根是x= 2$,则a的值为(D)
A.$\frac{5}{2}$
B.$-\frac{3}{2}$
C.$-\frac{5}{2}或\frac{3}{2}$
D.$\frac{5}{2}或-\frac{3}{2}$

答案： 【解析】：
本题主要考查了一元二次方程的求解以及方程的根的定义。
首先，将$x = 2$代入方程$(ax - 1)^{2} - 16 = 0$中，
得到$(2a - 1)^{2} - 16 = 0$，
进一步展开，得到$(2a - 1)^{2} = 16$，
对方程两边同时开平方，得到$2a - 1 = \pm 4$，
解出$a$，得到两个$a = \frac{5}{2}$或$a = - \frac{3}{2}$。
【答案】：
D. $\frac{5}{2}$或$-\frac{3}{2}$。

10. 若关于x的方程$(x+1)^{2}= k-2$有实数根,则k的取值范围是$k \geq 2$.

答案： 【解析】：
首先，我们有方程 $(x+1)^{2} = k-2$。
为了找到 $k$ 的取值范围，我们需要确保方程有实数根。
根据平方根的性质，一个数的平方总是非负的，即 $(x+1)^{2} \geq 0$。
因此，为了使方程有实数根，我们需要 $k-2 \geq 0$。
解这个不等式，我们得到 $k \geq 2$。
【答案】：
$k \geq 2$

11. (新情境·运算程序)如图所示为一个简单的数值运算程序,则输入的x的值为______.

1±√3

答案： 【解析】：本题可根据数值运算程序列出关于$x$的方程，然后通过求解方程得到$x$的值。
根据数值运算程序可知，输入$x$后，先计算$(x - 1)^2$，再将结果乘以$-3$，最后输出$-9$，所以可列出方程$(x - 1)^2×(-3)= - 9$。
求解该方程时，可先两边同时除以$-3$，得到$(x - 1)^2$的值，再对等式两边开平方，进而求出$x$的值。
【答案】：解：由题意得$(x - 1)^2×(-3)= - 9$，
两边同时除以$-3$可得：$(x - 1)^2 = (-9)÷(-3)=3$，
两边同时开平方可得：$x - 1 = \pm\sqrt{3}$，
移项可得：$x = 1\pm\sqrt{3}$。
故答案为$1\pm\sqrt{3}$。

12. 若关于x的一元二次方程$ax^{2}= b(ab＞0)的两个不等的实数根分别是x_{1}= m-1,x_{2}= 2m+4$,则m的值是______-1。

答案： 【解析】：
本题考查了一元二次方程的求解以及配方法的应用。
首先，我们将原方程$ax^{2} = b$转化为标准形式，即$x^{2} = \frac{b}{a}$。
由于$ab ＞ 0$，所以方程有两个不相等的实数根，分别为$\sqrt{\frac{b}{a}}$和$-\sqrt{\frac{b}{a}}$。
根据题目条件，这两个根分别等于$m - 1$和$2m + 4$。
由于一元二次方程的根互为相反数，所以有：
$m - 1 + 2m + 4 = 0$，
解这个方程，我们得到：
$3m + 3 = 0$，
$m = -1$，
另外，由于方程的根是实数，所以判别式$\Delta$必须大于0。但在这个特定问题中，由于$ab ＞ 0$，判别式已经隐含地满足了。不过，我们还需要确保$m - 1$和$2m + 4$不相等，以符合题目中“两个不等的实数根”的条件。将$m = -1$代入，得到$m - 1 = -2$和$2m + 4 = 2$，两者不相等，满足条件。
【答案】：
$m = -1$。

13. (易错题)已知关于x的方程$a(x+m)^{2}+p= 0$(a,m,p为常数,$a≠0$)的两个根分别是$x_{1}= 1,x_{2}= -3$,则关于x的方程$a(x+m+3)^{2}+p= 0$的根为______$x_{1}=-2$，$x_{2}=-6$.

答案： 【解析】：
本题主要考查一元二次方程的根的性质以及方程的平移变换。
首先，我们已知方程 $a(x+m)^{2}+p= 0$ 的两个根为 $x_{1}= 1$ 和 $x_{2}= -3$。
现在，我们要求解方程 $a(x+m+3)^{2}+p= 0$ 的根。
观察两个方程，我们发现第二个方程相对于第一个方程，$x$ 的每一个取值都增加了 3（即 $x$ 替换为 $x+3$）。
因此，我们可以将第一个方程的根 $x_{1}= 1$ 和 $x_{2}= -3$ 分别减去 3，以得到第二个方程的根。
具体地，对于第一个方程的根 $x_{1}= 1$，我们有：
$x_{1}^{\prime} = 1 - 3 = -2$
对于第一个方程的根 $x_{2}= -3$，我们有：
$x_{2}^{\prime} = -3 - 3 = -6$
所以，方程 $a(x+m+3)^{2}+p= 0$ 的两个根为 $x_{1}^{\prime}= -2$ 和 $x_{2}^{\prime}= -6$。
【答案】：
$x_{1}= -2, x_{2}= -6$

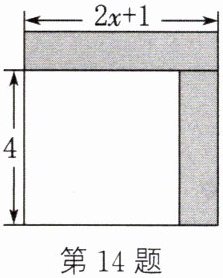
14. (新视角·操作实践题)如图,将边长为$2x+1$的正方形沿两边剪去宽相同的矩形,剩下的部分是一个边长为4的正方形.若剪去部分(涂色部分)的面积为9,求x的值.

答案： 【解析】：
本题考查一元二次方程的应用，通过已知条件找出等量关系列出方程，进而求解$x$的值。
已知原正方形边长为$2x + 1$，剩下部分是边长为$4$的正方形，且剪去部分面积为$9$。
原正方形面积$S_1=(2x + 1)^2$，剩下正方形面积$S_2 = 4^2=16$。
根据原正方形面积$=$剩下正方形面积$+$剪去部分面积，可列出方程$(2x + 1)^2=16 + 9$。
接下来求解这个方程：
$\begin{aligned}(2x + 1)^2&=16 + 9\\(2x + 1)^2&=25\\2x+1&=\pm5\end{aligned}$
当$2x + 1 = 5$时，$2x=5 - 1$，$2x = 4$，解得$x = 2$；
当$2x + 1 = -5$时，$2x=-5 - 1$，$2x = -6$，解得$x = -3$。
因为边长不能为负，$x=-3$时，$2x+1=2×(-3)+1=-5\lt0$，不符合实际情况，应舍去。
【答案】：
解：$(2x + 1)^2=4^2 + 9$
$(2x + 1)^2=25$
$2x + 1=\pm5$
当$2x + 1 = 5$时，$x = 2$；
当$2x + 1 = -5$时，$x = -3$（舍去）。
所以$x$的值为$2$。

15. 对于实数p,q,我们用符号$min\{ p,q\}$表示p,q两数中较小的数,如$min\{ 1,2\} = 1,min\{ -\sqrt{2},-\sqrt{3}\} = -\sqrt{3},min\{ 2,2\} = 2$.若$min\{ (x-1)^{2},x^{2}\} = 1$,求x的值.

答案： 解：分两种情况讨论：
情况一：当$(x-1)^2 \leq x^2$时，$min\{(x-1)^2, x^2\}=(x-1)^2$，则$(x-1)^2=1$
开平方得$x-1=\pm1$
解得$x_1=2$，$x_2=0$
验证$(x-1)^2 \leq x^2$：
当$x=2$时，$(2-1)^2=1$，$2^2=4$，$1 \leq 4$，成立；
当$x=0$时，$(0-1)^2=1$，$0^2=0$，$1 \leq 0$，不成立，舍去。
情况二：当$(x-1)^2 ＞ x^2$时，$min\{(x-1)^2, x^2\}=x^2$，则$x^2=1$
开平方得$x=\pm1$
验证$(x-1)^2 ＞ x^2$：
当$x=1$时，$(1-1)^2=0$，$1^2=1$，$0 ＞ 1$，不成立，舍去；
当$x=-1$时，$(-1-1)^2=4$，$(-1)^2=1$，$4 ＞ 1$，成立。
综上，$x$的值为$2$或$-1$。