《2025年金钥匙课时学案作业本九年级数学上册人教版》

10. 已知二次函数$y= (x - m)^{2}-1$(m为常数),当自变量x分别取-1,2时,所对应的y值相等,则m的值为$\frac{1}{2}$.

答案： 解：当$x=-1$时，$y=(-1 - m)^{2}-1=(m + 1)^{2}-1$；
当$x=2$时，$y=(2 - m)^{2}-1$。
因为所对应的$y$值相等，所以$(m + 1)^{2}-1=(2 - m)^{2}-1$，
即$(m + 1)^{2}=(2 - m)^{2}$，
展开得$m^{2}+2m + 1 = m^{2}-4m + 4$，
移项合并同类项得$6m = 3$，
解得$m=\frac{1}{2}$。
$\frac{1}{2}$

11. 已知二次函数$y= (x - 2a)^{2}+a - 1$(a为常数),当a取不同的值时,其图象构成一个“抛物线系”.如图所示为当$a= -1,a = 0,a = 1,a = 2$时二次函数的图象,它们的顶点在一条直线上,则这条直线对应的函数解析式为$y= $$\frac{1}{2}x - 1$.

答案： 【解析】：本题可先根据二次函数顶点式求出不同$a$值时函数的顶点坐标，再设出直线解析式，将顶点坐标代入解析式求出直线解析式。
对于二次函数$y=(x - 2a)^{2}+a - 1$，其顶点式为$y=a(x-h)^2+k$（$a\neq0$，$(h,k)$为顶点坐标）的形式，所以该二次函数的顶点坐标为$(2a,a - 1)$。
分别计算$a = - 1$，$a = 0$，$a = 1$，$a = 2$时二次函数的顶点坐标：
当$a = - 1$时，$2a=2×(-1)= - 2$，$a - 1=-1 - 1=-2$，顶点坐标为$( - 2,-2)$。
当$a = 0$时，$2a=2×0 = 0$，$a - 1=0 - 1=-1$，顶点坐标为$(0,-1)$。
当$a = 1$时，$2a=2×1 = 2$，$a - 1=1 - 1=0$，顶点坐标为$(2,0)$。
当$a = 2$时，$2a=2×2 = 4$，$a - 1=2 - 1=1$，顶点坐标为$(4,1)$。
设这条直线对应的函数解析式为$y = kx + b$（$k\neq0$），因为顶点$(0,-1)$，$(2,0)$在直线上，将$(0,-1)$，$(2,0)$代入$y = kx + b$可得方程组$\begin{cases}b = - 1\\2k + b = 0\end{cases}$。
将$b = - 1$代入$2k + b = 0$，可得$2k - 1 = 0$，移项可得$2k=1$，解得$k=\frac{1}{2}$。
所以直线解析式为$y=\frac{1}{2}x - 1$。
【答案】：$\frac{1}{2}x - 1$

12. (2023·通州期中)已知二次函数$y= (x - 2)^{2}+k$的图象与y轴的交点坐标为$(0,3)$.若函数值$y＜3$,则自变量x的取值范围是$0 \lt x \lt 4$.

答案： 【解析】：
首先，我们需要确定二次函数的具体形式。题目给出了二次函数与y轴的交点坐标，我们可以通过这个坐标来确定函数中的未知数k。
接着，我们需要找出函数值y小于3时，自变量x的取值范围。这需要我们利用二次函数的性质，特别是其对称性和开口方向，来进行分析和计算。
二次函数$y= (x - 2)^{2}+k$的对称轴为$x=2$，由于二次项系数为正，所以函数开口向上，即函数在对称轴左侧是减函数，在对称轴右侧是增函数。
已知函数与y轴的交点坐标为$(0,3)$，代入函数方程可得：
$3 = (0 - 2)^{2}+k$，
$3 = 4 + k$，
解得：$k = -1$。
所以，二次函数的具体形式为$y= (x - 2)^{2}-1$。
接下来，我们需要找出函数值y小于3时，自变量x的取值范围。即解不等式：
$(x - 2)^{2}-1 \lt 3$，
移项得：
$(x - 2)^{2} \lt 4$，
开方得：
$-2 \lt x - 2 \lt 2$，
进一步解得：
$0 \lt x \lt 4$。
但由于二次函数开口向上，且对称轴为$x=2$，所以函数在$x=0$和$x=4$时取得相同的函数值，而在$x=2$时取得最小值。因此，当$y\lt3$时，自变量x的取值范围应为$0\lt x\lt4$中除去使得$y=3$的$x$值，而由于对称性，这部分$x$值就是$x=0$和$x=4$，但$x=0$和$x=4$时$y=3$，不满足$y\lt3$的条件，所以自变量x的取值范围就是$0\lt x\lt4$。
但由于我们之前已经通过不等式解出了这个范围，所以这一步的验证是多余的。
【答案】：
自变量$x$的取值范围是$0 \lt x \lt 4$。

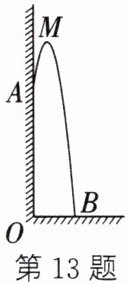
13. (数学建模思想)如图,从某幢建筑物10m高的窗口A处用水管向外喷水,喷出的水是抛物线形(抛物线所在平面与地面垂直),抛物线的最高点M离墙1m,离地面$\frac{40}{3}m$.
(1) 建立适当的平面直角坐标系,求抛物线对应的函数解析式;
(2) 求水的落地点B与点O之间的距离.
]

答案： 【解析】：
本题可根据二次函数的顶点式来求解抛物线的函数解析式，再通过令函数值$y = 0$求出落地点$B$的横坐标，进而求出$OB$的距离。
（1）求抛物线对应的函数解析式
步骤一：建立平面直角坐标系
以$O$为原点，$OA$所在直线为$y$轴，$OB$所在直线为$x$轴建立平面直角坐标系。
步骤二：确定抛物线的顶点坐标
已知抛物线的最高点$M$离墙$1m$，离地面$\frac{40}{3}m$，所以顶点$M$的坐标为$(1,\frac{40}{3})$。
步骤三：设抛物线的函数解析式
因为抛物线的顶点式为$y=a(x - h)^2 + k$（$a\neq0$，$(h,k)$为顶点坐标），所以设抛物线的函数解析式为$y=a(x - 1)^2 + \frac{40}{3}$。
步骤四：求出$a$的值
已知窗口$A$处离地面$10m$，即点$A$的坐标为$(0,10)$，将点$A(0,10)$代入$y=a(x - 1)^2 + \frac{40}{3}$可得：
$10=a(0 - 1)^2 + \frac{40}{3}$
$10=a + \frac{40}{3}$
$a=10 - \frac{40}{3}=-\frac{10}{3}$
步骤五：写出抛物线的函数解析式
将$a=-\frac{10}{3}$代入$y=a(x - 1)^2 + \frac{40}{3}$，得到抛物线的函数解析式为$y=-\frac{10}{3}(x - 1)^2 + \frac{40}{3}$，展开可得$y=-\frac{10}{3}x^2+\frac{20}{3}x + 10$。
（2）求水的落地点$B$与点$O$之间的距离
步骤一：令$y = 0$，求出$x$的值
当水落到地面时，$y = 0$，即$-\frac{10}{3}(x - 1)^2 + \frac{40}{3}=0$，
两边同时乘以$-\frac{3}{10}$可得$(x - 1)^2 - 4 = 0$，
移项可得$(x - 1)^2 = 4$，
开平方可得$x - 1 = \pm2$，
当$x - 1 = 2$时，$x = 3$；当$x - 1 = -2$时，$x = -1$（因为距离不能为负，舍去）。
步骤二：确定$OB$的距离
因为点$B$在$x$轴正半轴上，所以$OB$的距离就是点$B$的横坐标的绝对值，即$OB = 3m$。
【答案】：
(1) 抛物线的函数解析式为$y=-\frac{10}{3}(x - 1)^2 + \frac{40}{3}$（或$y=-\frac{10}{3}x^2+\frac{20}{3}x + 10$）；
(2) 水的落地点$B$与点$O$之间的距离为$3m$。

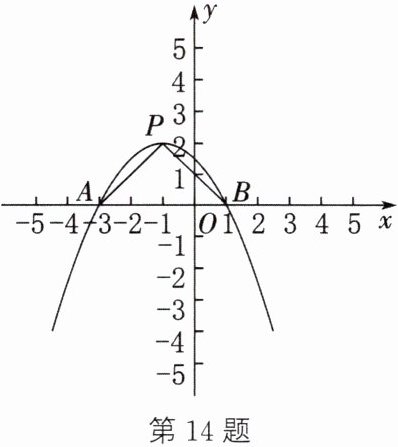
14. (数形结合思想)如图,抛物线$y = a(x + 1)^{2}+2$与x轴交于A,B两点,且点A的坐标为$(-3,0)$.
(1) 求a的值和点B的坐标.
(2) 设抛物线的顶点为P,连接PA,PB,试求$\triangle PAB$的面积.
(3) 在抛物线上是否存在点M,使得$\triangle MAB的面积是\triangle PAB$的面积的2倍?若存在,求出点M的坐标;若不存在,请说明理由.
]

答案： 【解析】：
(1) 要求a的值和点B的坐标，需要利用已知点A的坐标$(-3,0)$代入抛物线方程$y = a(x + 1)^{2} + 2$，解出a的值，再求出抛物线与x轴的另一个交点B的坐标。
(2) 要求$\triangle PAB$的面积，需要先确定顶点P的坐标，然后利用三角形面积公式求解。
(3) 要判断在抛物线上是否存在点M，使得$\triangle MAB$的面积是$\triangle PAB$的面积的2倍，需要先求出$\triangle PAB$的面积，然后设出点M的坐标，通过面积公式反推出点M的坐标。
【答案】：
(1) 将点$A(-3,0)$代入$y = a(x + 1)^{2} + 2$，得到方程：
$0 = a(-3 + 1)^{2} + 2$
$0 = 4a + 2$
解得：
$a = -\frac{1}{2}$
所以，抛物线的解析式为：
$y = -\frac{1}{2}(x + 1)^{2} + 2$
令$y=0$，则$0 = -\frac{1}{2}(x + 1)^{2} + 2$，
移项得：
$\frac{1}{2}(x + 1)^{2} = 2$
两边同时乘以2得：
$(x + 1)^{2} = 4$
开方得：
$x + 1 = \pm 2$
解得：
$x_{1} = 1, x_{2} = -3$
由于点A的横坐标为-3，所以点B的坐标为$(1,0)$。
(2) 抛物线的顶点式为$y = -\frac{1}{2}(x + 1)^{2} + 2$，所以顶点P的坐标为$(-1,2)$。
根据三角形面积公式，$\triangle PAB$的面积为：
$S_{\triangle PAB} = \frac{1}{2} × AB × 高$
其中，$AB = 1 - (-3) = 4$，高为点P到x轴的距离，即2。
所以，
$S_{\triangle PAB} = \frac{1}{2} × 4 × 2 = 4$
(3) 假设存在点$M(x,y)$使得$\triangle MAB$的面积是$\triangle PAB$的面积的2倍，即8。
根据三角形面积公式，有：
$S_{\triangle MAB} = \frac{1}{2} × AB × |y| = 8$
由于$AB = 4$，所以：
$|y| = 4$
即$y = \pm 4$。
将$y = 4$代入抛物线方程$y = -\frac{1}{2}(x + 1)^{2} + 2$，得到方程：
$4 = -\frac{1}{2}(x + 1)^{2} + 2$
移项并整理得：
$(x + 1)^{2} = -4$
此方程无实数解。
将$y = -4$代入抛物线方程，得到方程：
$-4 = -\frac{1}{2}(x + 1)^{2} + 2$
移项并整理得：
$(x + 1)^{2} = 12$
开方得：
$x + 1 = \pm 2\sqrt{3}$
解得：
$x_{1} = 2\sqrt{3} - 1, x_{2} = -2\sqrt{3} - 1$
所以，存在两个点M，其坐标分别为$(2\sqrt{3} - 1, -4)$和$(-2\sqrt{3} - 1, -4)$。