《2025年金钥匙课时学案作业本九年级数学上册人教版》

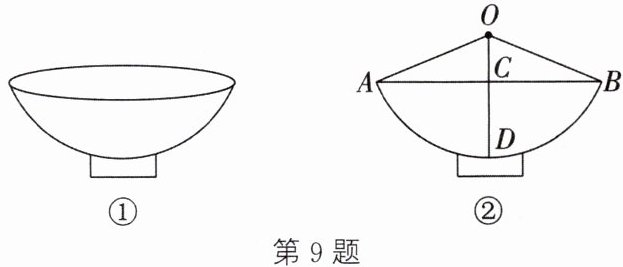
9. (新考向·传统文化)(2023·陕西)陕西饮食文化源远流长,“老碗面”是陕西地方特色美食之一.如图②所示为从正面看到的一个“老碗”(如图①)的形状示意图.$\overset{\frown}{AB}是\odot O$的一部分,$D是\overset{\frown}{AB}$的中点,连接$OD$,与弦$AB交于点C$,连接$OA$,$OB$.已知$AB = 24\mathrm{cm}$,碗深$CD = 8\mathrm{cm}$,则$\odot O的半径OA$为( )A

A.$13\mathrm{cm}$
B.$16\mathrm{cm}$
C.$17\mathrm{cm}$
D.$26\mathrm{cm}$
]

答案： 【解析】：本题可根据垂径定理以及勾股定理来求解$\odot O$的半径$OA$。
步骤一：根据垂径定理求出$AC$的长度
垂径定理是指垂直于弦的直径平分弦且平分这条弦所对的两条弧。
已知$D$是$\overset{\frown}{AB}$的中点，$OD$是半径，所以$OD\perp AB$，$AB = 24cm$，根据垂径定理可得$AC=\frac{1}{2}AB=\frac{1}{2}×24 = 12cm$。
步骤二：设$\odot O$的半径为$R$，表示出$OC$的长度
设$\odot O$的半径为$R cm$，已知碗深$CD = 8cm$，因为$OC=OD - CD$，$OD$为半径$R$，所以$OC=(R - 8)cm$。
步骤三：在$Rt\triangle AOC$中，根据勾股定理列方程求解$R$
在$Rt\triangle AOC$中，$OA$为斜边，$AC$和$OC$为两直角边，根据勾股定理$a^2+b^2=c^2$（其中$a$、$b$为直角边，$c$为斜边）可得：
$AC^{2}+OC^{2}=OA^{2}$，即$12^{2}+(R - 8)^{2}=R^{2}$。
展开方程可得：
$144 + R^{2}-16R + 64 = R^{2}$。
移项化简可得：
$16R = 208$，
解得$R = 13$。
所以$\odot O$的半径$OA$为$13cm$，答案选A。
【答案】：A

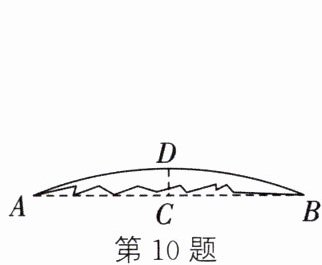
10. (教材 P82 例 2 变式)某圆形玻璃镜面碎成了几块,其中一块如图所示,测得弦$AB的长为20\mathrm{cm}$,弓形的高$CD为2\mathrm{cm}$,则该圆形玻璃镜面的半径为______$\mathrm{cm}$.
]

26

答案： 【解析】：
本题要求圆的半径，已知弦$AB$的长为$20\mathrm{cm}$，弓形的高$CD$为$2\mathrm{cm}$，我们可以通过连接圆心和弦的中点，构造直角三角形，利用勾股定理求解。
设圆心为$O$，半径为$r$，连接$OA$，由于$CD$垂直于$AB$且平分$AB$（垂径定理），所以$AC = \frac{AB}{2} = 10\mathrm{cm}$，$OC = r - CD = r - 2\mathrm{cm}$。
在直角三角形$OAC$中，根据勾股定理，有$OA^2 = AC^2 + OC^2$，即$r^2 = 10^2 + (r - 2)^2$。
展开并整理得：$r^2 = 100 + r^2 - 4r + 4$。
进一步整理得：$4r = 104$。
解得：$r = 26 ÷ 2 = 26\mathrm{cm}$（负值舍去，因为半径不能为负）。
【答案】：
$26$

11. 已知$\odot O的直径CD = 10$,$AB是\odot O$的弦,$AB\perp CD$,垂足为$M$,$OM:OC = 3:5$,则$AC$的长为$2\sqrt{5}$或$4\sqrt{5}$.

答案： 解：
∵CD是直径，CD=10，
∴OC=OD=5，圆心O为CD中点。
∵OM:OC=3:5，
∴OM=3。
情况1：点M在OC上
∵AB⊥CD，
∴AM=√(OA²-OM²)=√(5²-3²)=4。
∵CM=OC-OM=5-3=2，
∴AC=√(AM²+CM²)=√(4²+2²)=2√5。
情况2：点M在OD上
∵OM=3，
∴CM=OC+OM=5+3=8。
∵AM=4（同情况1），
∴AC=√(AM²+CM²)=√(4²+8²)=4√5。
综上，AC的长为2√5或4√5。

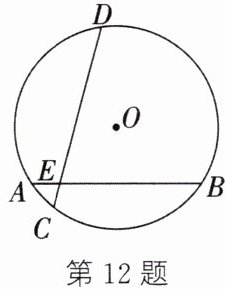
12. 如图,在半径为$\sqrt{13}的\odot O$中,弦$AB$,$CD交于点E$,$\angle DEB = 75^{\circ}$,$AB = 6$,$AE = 1$,求$CD$的长.
]

答案： 解：过点O作OM⊥AB于M，ON⊥CD于N，连接OB，OD。
∵AB=6，AE=1，
∴EB=AB-AE=5，AM=MB=3，ME=AM-AE=2。
∵OM⊥AB，OB=√13，
∴OM=√(OB²-MB²)=√(13-9)=2。
∵∠DEB=75°，OM⊥AB，ON⊥CD，
∴∠ONE=∠OME=90°，∠MON=180°-75°=105°。
在Rt△OME中，OM=2，ME=2，
∴∠OME=90°，∠OEM=45°，OE=√(OM²+ME²)=2√2。
在△ONE中，∠OEN=∠DEB-∠OEM=30°，ON=OE·sin30°=2√2×(1/2)=√2。
∵ON⊥CD，OD=√13，
∴DN=√(OD²-ON²)=√(13-2)=√11，CD=2DN=2√11。
答：CD的长为2√11。

13. (新情境·日常生活)现有一座拱桥,桥下水面宽度$AB是16$米,拱高$CD是4$米.
(1) 若把拱桥看成抛物线的一部分,建立如图①所示的平面直角坐标系.
① 当水面上升$3米至EF$时,$EF = $8米;
② 一艘宽为$4$米,高为$3.5$米的船能否通过该拱桥(船的吃水深度忽略不计)?能通过
(2) 如图②,若把拱桥看成圆的一部分,一艘船在水面上的高度为$3.5$米,则船的宽度不能超过多少米,才能使船顺利通过拱桥(结果保留根号)?$\sqrt{39}$米

答案：
(1)①设抛物线解析式为$y = ax^2 + 4$，将$B(8,0)$代入得$0 = 64a + 4$，解得$a=-\frac{1}{16}$，所以$y=-\frac{1}{16}x^2 + 4$。水面上升3米时，$y=3$，则$3=-\frac{1}{16}x^2 + 4$，$x^2=16$，$x=\pm4$，$EF=8$米。
②船宽4米，当$x=2$时，$y=-\frac{1}{16}×4 + 4=3.75$米，$3.75＞3.5$，能通过。
(2)设圆的半径为$r$，则$(r - 4)^2 + 8^2=r^2$，解得$r=10$。船高3.5米时，$CD=4$米，$OD=10 - 4=6$米，$OE=10$米，$CE=\sqrt{10^2 - (6 + 3.5)^2}=\sqrt{100 - 90.25}=\sqrt{9.75}=\frac{\sqrt{39}}{2}$米，船宽不超过$\sqrt{39}$米。
(1)①8；②能通过；
(2)$\sqrt{39}$米。