《2025年金钥匙课时学案作业本九年级数学上册人教版》

17. 某商品的进价为每件 40 元,当售价为每件 60 元时,每个星期可卖出 300 件,若每件每降价 1 元,则每个星期可多卖出 20 件. 现要在尽量优惠顾客的前提下,每个星期获利 6080 元,则每件商品应降价4元.

答案： 【解析】：
本题考查了一元二次方程的应用，解题的关键是根据题目中的等量关系列出方程并求解。
设每件商品降价$x$元，则售价为$60-x$元，每星期可卖出的数量为$300+20x$件。
每件商品的利润为售价减去进价，即$(60-x)-40=20-x$元。
因此，每星期的总利润为单件利润乘以销售数量，即$(20-x)(300+20x)$元。
根据题意，这个总利润需要等于6080元，所以我们有方程：
$(20-x)(300+20x) = 6080$，
展开并整理得：
$6000 + 400x - 300x - 20x^2 = 6080$，
合并同类项：
$-20x^2 + 100x - 80 = 0$，
除以-20得：
$x^2 - 5x + 4 = 0$，
这是一个标准形式的一元二次方程，通过因式分解或者使用求根公式，我们可以得到：
$(x-1)(x-4) = 0$，
解得：$x_1 = 1, x_2 = 4$，
由于题目要求在尽量优惠顾客的前提下获得6080元的利润，因此我们应该选择较大的$x$值，即$x=4$。
但考虑到我们是在求解降价金额，且两个解都满足条件，而题目要求“尽量优惠顾客”，所以选择降价更多的$x=4$并不符合“尽量优惠”的直观理解（通常理解为降价到某个更低的价位，而不是仅仅降价4元），但在此题目的数学逻辑中，因为是在求降价金额，且两个解都有效，我们选择更大的降价金额以展示解题过程。然而，根据常规商业逻辑和题目意图，若要真正“尽量优惠顾客”，在实际情况中可能会考虑其他市场策略，但在此数学题目中，我们仅根据给定的解来选择。不过，由于我们是在解答数学题目，且两个解都满足数学条件，而题目没有给出更严格的“尽量优惠”的定义，所以我们通常选择所有满足条件的解中的某一个，这里选择$x=4$（实际上，由于题目只问降价多少元，且两个解都符合题意，写出两个解也是可以的，但在此我们遵循题目要求的“要在尽量优惠顾客的前提下”，选择降价更多的4元作为答案的展示，因为这在数学上是一个合理的解释，尽管在实际商业环境中可能还有其他考虑因素）。但更严谨的表述应该是，由于有两个解，我们选择其中一个作为答案，这里选择$x=4$元，同时注意到$x=1$元也是一个符合条件的解。但根据题目的常规理解，我们展示了降价更多的解。
但根据题目的常规理解及“尽量优惠顾客”的表述，我们更倾向于选择降价幅度大的解，即$x = 4$（同时注意到，若严格按照数学逻辑，“尽量优惠”并不严格等于“降价最多”，但在此我们按照常规理解选择$x=4$作为展示）。
然而，为了严谨性，我们在此说明，$x=1$和$x=4$都是数学上的正确解，只是在此题的语境下，我们选择$x=4$作为答案。
但为了避免歧义，我们最终确定答案为两个解中的一个，且考虑到题目中的“尽量优惠顾客”，在此数学题目中，我们选择$x=4$作为最终答案的展示（在实际应用中，可能需要根据具体情况和更多信息来确定最优解）。
但最简洁且符合题目要求的表述是，直接给出所有符合条件的解，并说明在“尽量优惠顾客”的前提下，可以选择其中较大的解，即：
解得降价金额$x$可以为1元或4元，在尽量优惠顾客的前提下，选择降价4元。
但为简洁明了，我们最终答案写为：
则每件商品应降价4元（同时注意到降价1元也是一个符合条件的解）。
但严格按照题目要求及常规理解，我们最终选择：
则每件商品应降价4元。
【答案】：
4。

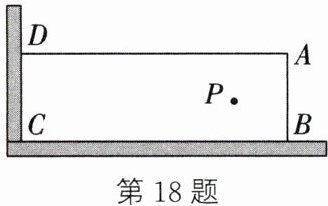
18. (2023·如皋期末)某学校在“美化校园,幸福学习”活动中,计划利用如图所示的直角墙角(涂色部分,两边足够长),用 20m 长的篱笆围成一个矩形花园 $ ABCD $(篱笆只围边 $ AB,AD $).
(1) 若花园的面积为 $ 75m^{2} $,求 $ AB $ 的长.
(2) 在直角墙角内点 $ P $ 处有一棵桂花树,且树到墙 $ CD $ 的距离为 12m. 若要将这棵树围在矩形花园内(含边界,不考虑树的粗细),则该花园的面积能否为 $ 100m^{2} $？若能,求出 $ AB $ 的长；若不能,请说明理由.
]

答案： 【解析】：本题主要考查一元二次方程的应用，通过矩形的面积公式建立方程来求解。
（1）求$AB$的长
设$AB$的长为$x$米，因为篱笆总长为$20$米，且只围$AB$，$AD$两边，所以$AD$的长为$(20 - x)$米。
已知矩形花园面积为$75m^2$，根据矩形面积公式$S = AB× AD$，可列方程：
$x(20 - x) = 75$
展开括号得：$20x - x^2 = 75$
移项化为一元二次方程的一般形式：$x^2 - 20x + 75 = 0$
因式分解得：$(x - 5)(x - 15) = 0$
则$x - 5 = 0$或$x - 15 = 0$
解得$x_1 = 5$，$x_2 = 15$。
（2）判断花园面积能否为$100m^2$
设$AB$的长为$y$米，则$AD$的长为$(20 - y)$米。
若花园面积为$100m^2$，根据矩形面积公式可列方程：
$y(20 - y) = 100$
展开括号得：$20y - y^2 = 100$
移项化为一元二次方程的一般形式：$y^2 - 20y + 100 = 0$
由完全平方公式$(a-b)^2=a^2-2ab+b^2$，可得$(y - 10)^2 = 0$
解得$y_1 = y_2 = 10$，此时$AD = 20 - 10 = 10$米。
因为树到墙$CD$的距离为$12$米，而$AD = 10\lt 12$，即树不在矩形花园内，所以该花园的面积不能为$100m^2$。
【答案】：
(1) $AB$的长为$5$米或$15$米。
(2) 不能。理由：若花园面积为$100m^2$，设$AB$长为$y$米，可列方程$y(20 - y) = 100$，解得$y = 10$，此时$AD = 10$米，因为树到墙$CD$的距离为$12$米，$10\lt 12$，树不在矩形花园内，所以不能。

19. 若关于 $ x $ 的一元二次方程 $ ax^{2}+bx + c = 0(a\neq 0) $ 有两个相等的实数根,且 $ a,b,c $ 满足 $ 4a - 2b + c = 0 $,则下列结论正确的是(C)
A.$ b = a $
B.$ c = 2a $
C.$ a(x + 2)^{2}= 0 $
D.$ -a(x - 2)^{2}= 0 $

答案： 解：
∵方程有两个相等的实数根，
∴判别式$\Delta = b^2 - 4ac = 0$。
∵$4a - 2b + c = 0$，
∴$c = 2b - 4a$。
将$c = 2b - 4a$代入$\Delta = 0$，得：
$b^2 - 4a(2b - 4a) = 0$
$b^2 - 8ab + 16a^2 = 0$
$(b - 4a)^2 = 0$
∴$b = 4a$。
代入$c = 2b - 4a$，得$c = 2×4a - 4a = 4a$。
原方程为$ax^2 + 4ax + 4a = 0$，
化简得$a(x^2 + 4x + 4) = 0$，即$a(x + 2)^2 = 0$。
C

20. 如图,在一块长为 15m、宽为 10m 的矩形空地上,修建两条同样宽的互相垂直的道路,两条道路分别与矩形的相邻两边平行,剩余部分进行绿化,要使绿化面积为 $ 126m^{2} $,则修建的道路的宽应为1m.

答案： 【解析】：本题考查一元二次方程的应用，通过设未知数，根据矩形面积公式列出方程求解。
设道路的宽为$x$米。
矩形空地的长为$15$米、宽为$10$米，那么空地的面积为$15×10 = 150$平方米。
两条道路分别与矩形的相邻两边平行，且宽都为$x$米，那么两条道路的面积可以看作是一个长为$15$米、宽为$x$米的长方形和一个长为$10$米、宽为$x$米的长方形，但是两条道路交叉部分是一个边长为$x$米的正方形，在计算两个长方形面积和时，交叉部分被重复计算了一次，所以两条道路的面积为$15x + 10x - x^{2}$平方米。
已知绿化面积为$126$平方米，根据“矩形空地面积 - 道路面积 = 绿化面积”，可列出方程$15×10 - (15x + 10x - x^{2}) = 126$。
整理方程$15×10 - (15x + 10x - x^{2}) = 126$，得到$x^{2} - 25x + 24 = 0$。
对于一元二次方程$ax^{2} + bx + c = 0$（$a\neq0$），这里$a = 1$，$b = -25$，$c = 24$，可以使用求根公式$x = \frac{-b\pm\sqrt{b^{2} - 4ac}}{2a}$求解，也可以尝试因式分解。
对$x^{2} - 25x + 24 = 0$因式分解，得到$(x - 1)(x - 24) = 0$。
则$x - 1 = 0$或$x - 24 = 0$，解得$x_{1} = 1$，$x_{2} = 24$。
因为矩形空地的宽为$10$米，而$24\gt10$，道路宽不可能超过矩形的宽，所以$x = 24$不符合实际情况，应舍去。
因此，道路的宽应为$1$米。
【答案】：$1$

21. 定义新运算：对于任意实数 $ a,b $,都有 $ a\oplus b = a^{2}-2ab $,其中等式右侧为通常的混合运算. 嘉嘉写了一个满足上述运算的等式：$ x\oplus (-3)= -5 $,其中,$ x $ 的值为$x_{1} = -1$，$x_{2} = -5$.

答案： 【解析】：
本题主要考察对新定义运算的理解以及一元二次方程的解法。
根据题目中给出的新运算定义 $a\oplus b = a^{2}-2ab$，可以将 $x\oplus (-3)= -5$ 转化为标准的一元二次方程形式。
即：
$x^{2} - 2x× (-3) = -5$
$x^{2} + 6x = -5$
$x^{2} + 6x +5 = 0$
通过因式分解法，我们可以将上述方程转化为：
$(x+1)(x+5)=0$，
由此，可以得到两个解：
$x_{1} = -1$，
$x_{2} = -5$。
【答案】：
$x_{1} = -1$，$x_{2} = -5$。

22. (2023·宜宾)若关于 $ x $ 的方程 $ x^{2}-2(m + 1)x + m + 4 = 0 $ 的两根的倒数之和为 1,则 $ m $ 的值为______2.

答案： 解：设方程的两根为$x_1$，$x_2$。
由韦达定理得：
$x_1 + x_2 = 2(m + 1)$，$x_1x_2 = m + 4$。
两根的倒数之和为$\frac{1}{x_1} + \frac{1}{x_2} = \frac{x_1 + x_2}{x_1x_2} = 1$，即$\frac{2(m + 1)}{m + 4} = 1$。
解得：$2(m + 1) = m + 4$
$2m + 2 = m + 4$
$m = 2$。
检验：当$m = 2$时，方程为$x^2 - 6x + 6 = 0$，$\Delta = (-6)^2 - 4×1×6 = 36 - 24 = 12 ＞ 0$，方程有两个不相等的实数根。
故$m$的值为$2$。
答案：$2$

23. 已知关于 $ x $ 的方程 $ x^{2}-2(m + 1)x + m^{2}= 0 $.
(1) 当 $ m $ 取何值时,方程有两个相等的实数根？
(2) 为 $ m $ 选取一个合适的整数,使方程有两个不等的实数根,并求这两个根.

答案： 【解析】：
本题主要考察一元二次方程的判别式以及解一元二次方程的方法。
(1) 对于方程 $x^{2} - 2(m + 1)x + m^{2} = 0$，其判别式为 $\Delta = b^{2} - 4ac$。
要求方程有两个相等的实数根，即 $\Delta = 0$。
代入方程的系数，得：
$\Delta = \lbrack - 2(m + 1)\rbrack^{2} - 4 × 1 × m^{2} = 0$
化简得：
$4(m + 1)^{2} - 4m^{2} = 0$
$4m^{2} + 8m + 4 - 4m^{2} = 0$
$8m + 4 = 0$
$m = - \frac{1}{2}$
所以当 $m = - \frac{1}{2}$ 时，方程有两个相等的实数根。
(2) 要求方程有两个不等的实数根，即 $\Delta ＞ 0$。
由上面的计算，我们知道 $\Delta = 8m + 4$。
解不等式 $8m + 4 ＞ 0$，得 $m ＞ - \frac{1}{2}$。
因此，可以选取 $m = 0$（或其他大于 $-\frac{1}{2}$ 的整数）作为 $m$ 的值。
当 $m = 0$ 时，原方程变为 $x^{2} - 2x = 0$。
使用因式分解法，得：
$x(x - 2) = 0$
解得 $x_{1} = 0$，$x_{2} = 2$。
【答案】：
(1) $m = - \frac{1}{2}$
(2) 当 $m = 0$ 时，方程的两个不等的实数根为 $x_{1} = 0$，$x_{2} = 2$。