《2025年金钥匙课时学案作业本九年级数学上册人教版》

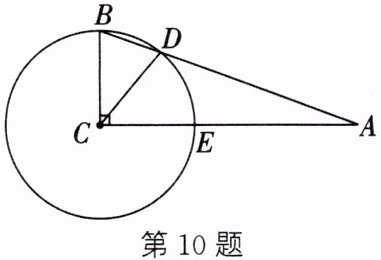
10. 如图,在 $ \mathrm{Rt} \triangle A B C $ 中,以点 $ C $ 为圆心,$ C B $ 为半径的圆交边 $ A B $ 于点 $ D $,交边 $ A C $ 于点 $ E $,$ \angle B C D= 40^{\circ} $,则 $ \angle A $ 的度数是______.
]

20°

答案： 解：
∵CB=CD，∠BCD=40°，
∴∠CBD=∠CDB=(180°-40°)/2=70°.
∵△ABC是直角三角形，∠ACB=90°，
∴∠A=90°-∠CBD=90°-70°=20°.
20°

11. 如图,$ C D $ 是 $ \odot O $ 的直径,$ \angle E O D= 84^{\circ} $,$ A $ 为 $ D C $ 的延长线上一点,$ A E $ 交 $ \odot O $ 于点 $ B $,且 $ A B= O C $,则 $ \angle A $ 的度数是______$28^{\circ}$.

答案： 【解析】：本题可根据圆的性质以及等腰三角形的性质，通过设未知数，利用三角形外角的性质建立方程来求解$\angle A$的度数。
步骤一：连接$OB$
因为$OB$、$OC$均为圆$O$的半径，所以$OB = OC$。
已知$AB = OC$，那么$AB = OB$，根据等腰三角形的性质可知，在等腰三角形中两底角相等，所以$\angle A = \angle AOB$。
设$\angle A = x$，则$\angle AOB = x$。
步骤二：求$\angle OBE$的度数
因为$OB = OE$（圆的半径相等），所以$\angle OEB = \angle OBE$。
根据三角形外角的性质：三角形的一个外角等于与它不相邻的两个内角之和，在$\triangle AOB$中，$\angle OBE$是$\triangle AOB$的一个外角，所以$\angle OBE=\angle A + \angle AOB = 2x$，即$\angle OEB = 2x$。
步骤三：求$\angle EOD$的度数
同样根据三角形外角的性质，在$\triangle AOE$中，$\angle EOD$是$\triangle AOE$的一个外角，所以$\angle EOD=\angle A + \angle OEB$。
已知$\angle EOD = 84^{\circ}$，$\angle A = x$，$\angle OEB = 2x$，则可列出方程$x + 2x = 84^{\circ}$。
步骤四：解方程求出$\angle A$的度数
解方程$x + 2x = 84^{\circ}$，即$3x = 84^{\circ}$，解得$x = 28^{\circ}$，所以$\angle A = 28^{\circ}$。
【答案】：$28^{\circ}$

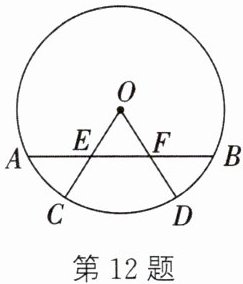
12. (易错题)如图,$ A B $ 是 $ \odot O $ 的弦,半径 $ O C $,$ O D $ 分别交 $ A B $ 于点 $ E $,$ F $,且 $ A E= B F $. 请你找出线段 $ O E $,$ O F $ 之间的数量关系,并给予证明.
]

答案： 解：OE=OF。
证明：过点O作OG⊥AB于点G。
∵OG⊥AB，
∴AG=BG（垂径定理）。
∵AE=BF，
∴AG - AE = BG - BF，即EG=FG。
∵OG⊥AB，
∴∠OGE=∠OGF=90°。
在△OGE和△OGF中，
∵EG=FG，∠OGE=∠OGF，OG=OG，
∴△OGE≌△OGF（SAS）。
∴OE=OF。

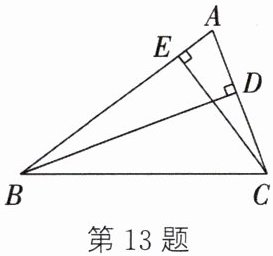
13. (教材 $ \mathrm{P} 81 $ 练习第 $ 3 $ 题变式)如图,在 $ \triangle A B C $ 中,$ B D $,$ C E $ 分别是边 $ A C $,$ A B $ 上的高. 求证：$ B $,$ C $,$ D $,$ E $ 四点在同一个圆上.
]

答案： 【解析】：
本题主要考查四点共圆的证明，特别是利用直角三角形斜边中线等于斜边一半这一性质来证明。
在直角三角形中，斜边上的中线长度等于斜边长度的一半，我们可以构造一个以BC为直径的圆，通过证明D、E都在这个圆上，从而证明B，C，D，E四点共圆。
【答案】：
证明：
连接$DE$，
∵$BD \perp AC$，$CE \perp AB$，
∴$\triangle BCD$和$\triangle BCE$都是直角三角形，且BC是它们的斜边，
取BC的中点为$O$，连接$OD$、$OE$，
∵在直角三角形中，斜边上的中线等于斜边的一半，
∴$OD = OE = \frac{1}{2}BC$，
∴点O是BC的中点，且到B、C、D、E四点的距离都等于$\frac{1}{2}BC$，
∴B，C，D，E四点在以O为圆心，BC为直径的圆上，
∴B，C，D，E四点共圆。

14. 如图,点 $ D $,$ E $ 分别在 $ \triangle A B C $ 的边 $ B C $,$ A B $ 上,过 $ D $,$ A $,$ C $ 三点的圆的圆心为 $ E $,过 $ B $,$ E $,$ F $ 三点的圆的圆心为 $ D $. 若 $ \angle C A B= 63^{\circ} $,求 $ \angle A B C $ 的度数.
]

答案： 解：连接CE，DE。
∵E是过A，C，D三点圆的圆心，
∴EA=EC=ED，
∴∠EAC=∠ECA，∠ECD=∠EDC。
∵∠CAB=63°，
∴∠EAC=63°，∠ECA=63°，
∴∠AEC=180°-∠EAC-∠ECA=54°。
∵D是过B，E，F三点圆的圆心，
∴DB=DE，
∴∠DBE=∠DEB。
设∠ABC=∠DBE=x，则∠DEB=x，∠EDB=180°-2x。
∵∠EDC=∠EDB=180°-2x，
∴∠ECD=∠EDC=180°-2x。
在△ABC中，∠ACB=∠ECA+∠ECD=63°+180°-2x=243°-2x。
∵∠CAB+∠ABC+∠ACB=180°，
∴63°+x+243°-2x=180°，
解得x=126°。
∵三角形内角不能大于180°，此解不合题意，舍去。
重新分析：∠EDB=180°-2x，∠EDC=180°-∠EDB=2x。
∴∠ECD=∠EDC=2x，∠ACB=∠ECA+∠ECD=63°+2x。
∵63°+x+63°+2x=180°，
∴3x=54°，x=18°。
答：∠ABC的度数为18°。