《2025年金钥匙课时学案作业本九年级数学上册人教版》

5. 如图,正方形 ABCD 与正方形$A_{1}B_{1}C_{1}D_{1}$关于某点成中心对称,A,$D_{1}$,D 三点的坐标分别是$(0,4),(0,3),(0,2)$.
(1) 求对称中心的坐标;
(2) 写出点 B,C,$B_{1},C_{1}$的坐标.

答案：
(1) 解：因为点$D_1$和点$D$关于对称中心对称，$D_1(0,3)$，$D(0,2)$，所以对称中心的纵坐标为$\frac{3 + 2}{2} = 2.5$，横坐标为$0$，对称中心坐标为$(0, 2.5)$。
(2) 解：因为$A(0,4)$，$D(0,2)$，所以正方形$ABCD$的边长为$4 - 2 = 2$，点$B$的坐标为$(-2,4)$，点$C$的坐标为$(-2,2)$。
设点$A_1$的坐标为$(x,y)$，因为点$A$和点$A_1$关于$(0,2.5)$对称，所以$\frac{0 + x}{2} = 0$，$\frac{4 + y}{2} = 2.5$，解得$x = 0$，$y = 1$，即$A_1(0,1)$。
正方形$A_1B_1C_1D_1$的边长为$2$，所以点$B_1$的坐标为$(2,1)$，点$C_1$的坐标为$(2,3)$。
综上，$B(-2,4)$，$C(-2,2)$，$B_1(2,1)$，$C_1(2,3)$。

6. (教材 P66 练习第 2 题变式)如图,在平面直角坐标系中,$\triangle ABC与\triangle A'B'C'关于点D(-1,0)$成中心对称.若点 A 的坐标为$(-3,-2)$,则点$A'$的坐标是 (B)

A.$(1,3)$
B.$(1,2)$
C.$(3,2)$
D.$(2,3)$

答案： 【解析】：本题可根据中心对称的性质来求解点$A'$的坐标。
关于中心对称的两个点，它们到对称中心的距离相等，且连线经过对称中心。
设点$A'$的坐标为$(x,y)$，已知点$A$的坐标为$(-3,-2)$，对称中心$D$的坐标为$(-1,0)$。
根据中点坐标公式：若有两点$M(x_1,y_1)$，$N(x_2,y_2)$，则它们的中点$P$的坐标为$(\frac{x_1 + x_2}{2},\frac{y_1 + y_2}{2})$。
因为点$D$是点$A$与点$A'$的中点，所以可得$\frac{-3 + x}{2}=-1$，$\frac{-2 + y}{2}=0$。
分别求解上述两个方程：
对于$\frac{-3 + x}{2}=-1$，等式两边同时乘以$2$可得$-3 + x = -2$，移项可得$x = -2 + 3 = 1$。
对于$\frac{-2 + y}{2}=0$，等式两边同时乘以$2$可得$-2 + y = 0$，移项可得$y = 2$。
所以点$A'$的坐标为$(1,2)$。
【答案】：B。

7. 已知$\triangle ABC与\triangle A_{1}B_{1}C_{1}$关于原点成中心对称,点 A,B,C 的对应点分别是$A_{1},B_{1},C_{1}$.若点 A 的坐标为$(1,2+m)$,点$A_{1}的坐标为(n,-3)$,则$m+n= $____.

答案： 【解析】：
由于$\triangle ABC$与$\triangle A_{1}B_{1}C_{1}$关于原点成中心对称，根据对称性质，点A和点$A_{1}$关于原点对称。
对于关于原点对称的两点，其横坐标和纵坐标都是互为相反数。
因此，点A的坐标$(1, 2+m)$和点$A_{1}$的坐标$(n, -3)$应满足：
$1 = -n$，
$2+m = -(-3)$，
解这两个方程，得到：
$n = -1$，
$m = 1$，
所以，$m+n = 1 + (-1) = 0$。
【答案】：
$0$。

8. 在如图所示的图案中,能够看成由“基本图案”绕中心旋转$180^{\circ }$得到的有 (B)
A.1个
B.2个
C.3个
D.4个

答案： 【解析】：
这道题考查的知识点是图形的旋转，特别是关于中心对称图形（即绕某一点旋转$180^{\circ}$后与原图重合的图形）的识别，
需要逐一观察每个图案，判断其是否可以通过某个“基本图案”绕中心旋转$180^{\circ}$得到，
第一个图案：
观察图案，它不是一个中心对称图形，因为无法找到一个点，使得图案绕这个点旋转$180^{\circ}$后与原图重合，
第二个图案：
这个图案可以看作是四个相同的圆围绕一个中心点排列而成，
通过绕中心点旋转$180^{\circ}$，图案会与原图重合，
因此，它是一个中心对称图形，
第三个图案：
这个图案由四个相同的直角三角形组成，它们围绕一个中心点排列，
通过绕中心点旋转$180^{\circ}$，图案也会与原图重合，
因此，它也是一个中心对称图形，
第四个图案：
这个图案由三个相同的叶片组成，它们围绕一个中心点排列，
但是，通过绕中心点旋转$180^{\circ}$，图案不会与原图重合，
因为它不是中心对称的，
综上所述，第二个和第三个图案是可以通过“基本图案”绕中心旋转$180^{\circ}$得到的，
因此，符合条件的图案有2个，
所以，这道题的答案是B，
【答案】：
B

9. 如图所示的图案都是在一个图案的基础上,在某画图软件中拖动一点后形成的,它们的共性是都可以由一个“基本图案”通过连续旋转得到,则旋转的角度可以是 (D)
A.$30^{\circ }$
B.$45^{\circ }$
C.$60^{\circ }$
D.$90^{\circ }$

答案： 【解析】：
本题可根据图形旋转的性质，通过观察图形中“基本图案”的数量，结合周角为$360^{\circ}$，来计算旋转的角度。
步骤一：分析图形中“基本图案”的数量
观察所给图形可知，每个图形都可以看作是由一个“基本图案”绕着某一点连续旋转得到的，且每个图形中“基本图案”的数量均为$4$个。
步骤二：计算旋转的角度
因为图形是绕着某一点连续旋转得到的，且旋转一周为$360^{\circ}$，现在一共有$4$个“基本图案”，即旋转了$4$次得到整个图形，所以每次旋转的角度为$360^{\circ}÷4 = 90^{\circ}$。
【答案】：D

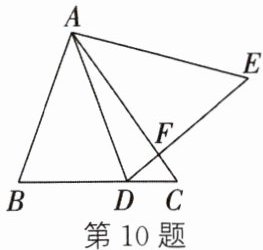
10. (2023·无锡)如图,在$\triangle ABC$中,$∠BAC= 55^{\circ }$,将$\triangle ABC$绕点 A 逆时针旋转$α(0^{\circ }＜α＜55^{\circ })$,得到$\triangle ADE$,DE 交 AC 于点 F.当$α=40^{\circ }$时,点 D 恰好落在边 BC 上,此时$∠AFE$的度数为 (B)

A.$80^{\circ }$
B.$85^{\circ }$
C.$90^{\circ }$
D.$95^{\circ }$

答案： 【解析】：本题主要考查了图形的旋转以及三角形内角和定理的运用。
由于$\triangle ABC$绕点A逆时针旋转了$40^\circ$得到$\triangle ADE$，
那么$AD=AB$，$AE=AC$，且$\angle DAB = \angle EAC = 40^\circ$，
又因为$\angle BAC = 55^\circ$，
所以$\angle DAF = \angle BAC - \angle EAC = 55^\circ - 40^\circ = 15^\circ$，
由于$AD = AB$，根据等腰三角形的性质，$\angle B = \angle ADB$，
利用三角形内角和为$180^\circ$，
可得$\angle B=\frac{180^\circ-\angle DAB}{2}=\frac{180^\circ-40^\circ}{2}=70^\circ$，
根据三角形的外角等于不相邻的两个内角和，
可得$\angle AFE = \angle DAF + \angle ADF= 15^\circ + 70^\circ= 85^\circ$。
【答案】：B。

11. 如图,正方形 OABC 的两边 OA,OC 分别在 x 轴、y 轴上,点$D(5,3)$在边 AB 上,以点 C 为中心,把$\triangle CDB旋转90^{\circ }$,则旋转后点 D 的对应点$D'$的坐标是 (C)
A.$(2,10)$
B.$(-2,0)$
C.$(2,10)或(-2,0)$
D.$(10,2)或(-2,0)$

答案： 解：
∵正方形OABC中，点D(5,3)在AB上，
∴OA=AB=BC=CO=5，点C(0,5)，B(5,5)，D(5,3)，
∴CD=√[(5-0)²+(3-5)²]=√29，CB=5，BD=5-3=2。
情况1：顺时针旋转90°
过D'作D'E⊥y轴于E，
∵∠BCD=∠D'CE，∠CBD=∠CED'=90°，CB=CO=5，
∴△CBD≌△CED'(AAS)，
∴CE=CB=5，D'E=BD=2，
∴OE=OC+CE=5+5=10，
∴D'(2,10)。
情况2：逆时针旋转90°
过D'作D'F⊥y轴于F，
同理△CBD≌△CFD'(AAS)，
∴CF=CB=5，D'F=BD=2，
∴OF=OC-CF=5-5=0，
∴D'(-2,0)。
综上，D'的坐标为(2,10)或(-2,0)。
答案：C