第43页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
7. (2024·崇川期中)在二次函数 $ y = a x ^ { 2 } + b x + c $ 中,$ x $ 与 $ y $ 的部分对应值如下表:
| $ x $ | …$ $ | $ - 3 $ | $ - 2 $ | $ - 1 $ | $ 0 $ | $ 1 $ | …$ $ |
| $ y $ | …$ $ | 13 | 6 | 1 | $ - 2 $ | $ - 3 $ | …$ $ |
根据表中信息,可得一元二次方程 $ a x ^ { 2 } + b x + c = 0 $ 的一个近似解 $ x _ { 1 } $ 的范围是 (
A.$ - 3 < x _ { 1 } < - 2 $
B.$ - 2 < x _ { 1 } < - 1 $
C.$ - 1 < x _ { 1 } < 0 $
D.$ 0 < x _ { 1 } < 1 $
| $ x $ | …$ $ | $ - 3 $ | $ - 2 $ | $ - 1 $ | $ 0 $ | $ 1 $ | …$ $ |
| $ y $ | …$ $ | 13 | 6 | 1 | $ - 2 $ | $ - 3 $ | …$ $ |
根据表中信息,可得一元二次方程 $ a x ^ { 2 } + b x + c = 0 $ 的一个近似解 $ x _ { 1 } $ 的范围是 (
C
)A.$ - 3 < x _ { 1 } < - 2 $
B.$ - 2 < x _ { 1 } < - 1 $
C.$ - 1 < x _ { 1 } < 0 $
D.$ 0 < x _ { 1 } < 1 $
答案:
解:由表格可知,当 $x = -1$ 时,$y = 1$;当 $x = 0$ 时,$y = -2$。
因为二次函数 $y = ax^2 + bx + c$ 的图像是一条抛物线,且当 $x = -1$ 时,$y = 1 > 0$;当 $x = 0$ 时,$y = -2 < 0$,所以抛物线在区间 $(-1, 0)$ 内与 $x$ 轴有一个交点。
因此,一元二次方程 $ax^2 + bx + c = 0$ 的一个近似解 $x_1$ 的范围是 $-1 < x_1 < 0$。
答案:C
因为二次函数 $y = ax^2 + bx + c$ 的图像是一条抛物线,且当 $x = -1$ 时,$y = 1 > 0$;当 $x = 0$ 时,$y = -2 < 0$,所以抛物线在区间 $(-1, 0)$ 内与 $x$ 轴有一个交点。
因此,一元二次方程 $ax^2 + bx + c = 0$ 的一个近似解 $x_1$ 的范围是 $-1 < x_1 < 0$。
答案:C
8. (2023·郴州)若抛物线 $ y = x ^ { 2 } - 6 x + c $ 与 $ x $ 轴只有一个公共点,则 $ c = $______
9
.
答案:
【解析】:
本题考查二次函数与$x$轴交点问题,涉及到一元二次方程根的判别式。
对于二次函数$y=ax^2+bx+c$,其与$x$轴交点即为一元二次方程$ax^2+bx+c=0$的根。
已知抛物线$y = x^{2} - 6x + c$与$x$轴只有一个公共点,这意味着对应的一元二次方程$x^{2} - 6x + c = 0$有且仅有一个实数根。
根据一元二次方程实数根的判别式的性质,当$\Delta=0$时,方程有且仅有一个实数根。
对于一元二次方程$ax^2+bx+c=0$($a\neq0$),其判别式$\Delta=b^2-4ac$。
在方程$x^{2} - 6x + c = 0$中,$a = 1$,$b = -6$,$c$为待求系数,代入判别式可得:
$\Delta=(-6)^2-4×1× c=36 - 4c$
因为方程有且仅有一个实数根,所以$\Delta=0$,即:
$36 - 4c = 0$
移项可得:
$4c = 36$
两边同时除以$4$,解得:
$c = 9$
【答案】:
$9$
本题考查二次函数与$x$轴交点问题,涉及到一元二次方程根的判别式。
对于二次函数$y=ax^2+bx+c$,其与$x$轴交点即为一元二次方程$ax^2+bx+c=0$的根。
已知抛物线$y = x^{2} - 6x + c$与$x$轴只有一个公共点,这意味着对应的一元二次方程$x^{2} - 6x + c = 0$有且仅有一个实数根。
根据一元二次方程实数根的判别式的性质,当$\Delta=0$时,方程有且仅有一个实数根。
对于一元二次方程$ax^2+bx+c=0$($a\neq0$),其判别式$\Delta=b^2-4ac$。
在方程$x^{2} - 6x + c = 0$中,$a = 1$,$b = -6$,$c$为待求系数,代入判别式可得:
$\Delta=(-6)^2-4×1× c=36 - 4c$
因为方程有且仅有一个实数根,所以$\Delta=0$,即:
$36 - 4c = 0$
移项可得:
$4c = 36$
两边同时除以$4$,解得:
$c = 9$
【答案】:
$9$
9. 若二次函数 $ y = x ^ { 2 } - 8 x + 5 c $ 的图象与 $ x $ 轴有两个公共点,则 $ c $ 的值可以是______
1
(填一个即可).
答案:
【解析】:
题目考查二次函数与$x$轴交点的性质,即对应的一元二次方程有两个不相等的实数根。
这需要判别式 $\Delta = b^{2} - 4ac > 0$。
对于给定的二次函数 $y = x^{2} - 8x + 5c$,
其中 $a = 1, b = -8, c$ 是我们需要找出的值(注意这里的$c$与题目中的$c$不同,为避免混淆,我们可以称题目中的$c$为$k$,即函数为$y = x^{2} - 8x + 5k$)。
将这些值代入判别式,得到:
$\Delta = (-8)^{2} - 4 × 1 × 5k = 64 - 20k$,
由于要求有两个不相等的实数根,所以:
$64 - 20k > 0$,
解这个不等式,得到:
$k < \frac{16}{5}$,
因此,$c$(或题目中的$k$)可以是小于$\frac{16}{5}$的任意实数。
为了简化,可以选择一个容易计算的数,如$c = 1$(注意这里将$k$换回题目中的$c$)。
【答案】:
1(答案不唯一,小于$\frac{16}{5}$的任意实数均可)。
题目考查二次函数与$x$轴交点的性质,即对应的一元二次方程有两个不相等的实数根。
这需要判别式 $\Delta = b^{2} - 4ac > 0$。
对于给定的二次函数 $y = x^{2} - 8x + 5c$,
其中 $a = 1, b = -8, c$ 是我们需要找出的值(注意这里的$c$与题目中的$c$不同,为避免混淆,我们可以称题目中的$c$为$k$,即函数为$y = x^{2} - 8x + 5k$)。
将这些值代入判别式,得到:
$\Delta = (-8)^{2} - 4 × 1 × 5k = 64 - 20k$,
由于要求有两个不相等的实数根,所以:
$64 - 20k > 0$,
解这个不等式,得到:
$k < \frac{16}{5}$,
因此,$c$(或题目中的$k$)可以是小于$\frac{16}{5}$的任意实数。
为了简化,可以选择一个容易计算的数,如$c = 1$(注意这里将$k$换回题目中的$c$)。
【答案】:
1(答案不唯一,小于$\frac{16}{5}$的任意实数均可)。
10. 已知二次函数 $ y = a x ^ { 2 } + b x - b - a $($ a, b $ 是常数,$ a \neq 0 $).
(1) 判断该二次函数的图象与 $ x $ 轴的交点的个数;
(2) 若该二次函数图象的对称轴是直线 $ x = - 1 $,求这个函数图象与 $ x $ 轴的交点的坐标.
(1) 判断该二次函数的图象与 $ x $ 轴的交点的个数;
(2) 若该二次函数图象的对称轴是直线 $ x = - 1 $,求这个函数图象与 $ x $ 轴的交点的坐标.
答案:
【解析】:
(1) 要判断二次函数与$x$轴的交点个数,我们需要计算判别式$\Delta = b^{2} - 4ac$,其中$a = a$,$b = b$,$c = -b-a$。
第一步,计算判别式$\Delta = b^{2} - 4a(-b-a) = b^{2} + 4ab + 4a^{2} = (2a + b)^{2}$。
第二步,根据判别式的性质,当$\Delta > 0$时,有两个不相等的交点;当$\Delta = 0$时,有两个相等的交点;当$\Delta < 0$时,没有交点。由于$(2a + b)^{2} \geq 0$,所以交点个数取决于$(2a + b)^{2}$是否大于0。
第三步,当$2a + b = 0$时,即$b = -2a$,$\Delta = 0$,函数图象与$x$轴有1个交点;当$2a + b \neq 0$时,即$b \neq -2a$,$\Delta > 0$,函数图象与$x$轴有2个交点。
(2) 若该二次函数图象的对称轴是直线$x = -1$,我们可以利用对称轴公式$x = -\frac{b}{2a}$来求解。
第一步,根据对称轴公式,我们有$-\frac{b}{2a} = -1$,解得$b = 2a$。
第二步,将$b = 2a$代入原函数,得到$y = ax^{2} + 2ax - 3a$。
第三步,令$y = 0$,得到方程$ax^{2} + 2ax - 3a = 0$,即$x^{2} + 2x - 3 = 0$(因为$a \neq 0$,所以可以除以$a$)。
第四步,解这个一元二次方程,得到$x_{1} = -3$,$x_{2} = 1$。
所以,这个函数图象与$x$轴的交点的坐标为$(-3, 0)$和$(1, 0)$。
【答案】:
(1) 当$b = -2a$时,函数图象与$x$轴有1个交点;当$b \neq -2a$时,函数图象与$x$轴有2个交点。
(2) 这个函数图象与$x$轴的交点的坐标为$(-3, 0)$和$(1, 0)$。
(1) 要判断二次函数与$x$轴的交点个数,我们需要计算判别式$\Delta = b^{2} - 4ac$,其中$a = a$,$b = b$,$c = -b-a$。
第一步,计算判别式$\Delta = b^{2} - 4a(-b-a) = b^{2} + 4ab + 4a^{2} = (2a + b)^{2}$。
第二步,根据判别式的性质,当$\Delta > 0$时,有两个不相等的交点;当$\Delta = 0$时,有两个相等的交点;当$\Delta < 0$时,没有交点。由于$(2a + b)^{2} \geq 0$,所以交点个数取决于$(2a + b)^{2}$是否大于0。
第三步,当$2a + b = 0$时,即$b = -2a$,$\Delta = 0$,函数图象与$x$轴有1个交点;当$2a + b \neq 0$时,即$b \neq -2a$,$\Delta > 0$,函数图象与$x$轴有2个交点。
(2) 若该二次函数图象的对称轴是直线$x = -1$,我们可以利用对称轴公式$x = -\frac{b}{2a}$来求解。
第一步,根据对称轴公式,我们有$-\frac{b}{2a} = -1$,解得$b = 2a$。
第二步,将$b = 2a$代入原函数,得到$y = ax^{2} + 2ax - 3a$。
第三步,令$y = 0$,得到方程$ax^{2} + 2ax - 3a = 0$,即$x^{2} + 2x - 3 = 0$(因为$a \neq 0$,所以可以除以$a$)。
第四步,解这个一元二次方程,得到$x_{1} = -3$,$x_{2} = 1$。
所以,这个函数图象与$x$轴的交点的坐标为$(-3, 0)$和$(1, 0)$。
【答案】:
(1) 当$b = -2a$时,函数图象与$x$轴有1个交点;当$b \neq -2a$时,函数图象与$x$轴有2个交点。
(2) 这个函数图象与$x$轴的交点的坐标为$(-3, 0)$和$(1, 0)$。
11. (新考法·综合与实践)某班数学兴趣小组对函数 $ y = x ^ { 2 } - 2 | x | $ 的图象和性质进行了探究,探究过程如下:
(1) 自变量 $ x $ 的取值范围是全体实数,$ x $ 与 $ y $ 的几组对应值如下表:
| $ x $ | …$ $ | $ - 3 $ | $ - \frac { 5 } { 2 } $ | $ - 2 $ | $ - 1 $ | $ 0 $ | $ 1 $ | $ 2 $ | $ \frac { 5 } { 2 } $ | $ 3 $ | …$ $ |
| $ y $ | …$ $ | 3 | $ \frac { 5 } { 4 } $ | 0 | $ - 1 $ | 0 | $ - 1 $ | $ m $ | $ \frac { 5 } { 4 } $ | 3 | …$ $ |
其中,$ m = $______.
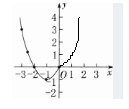
(2) 根据表中数据,在如图所示的平面直角坐标系中描点,现已画出了函数图象的一部分,请画出该函数图象的另一部分.
(3) 进一步探究函数图象发现:
① 方程 $ x ^ { 2 } - 2 | x | = 0 $ 有______个实数根;
② 若关于 $ x $ 的方程 $ x ^ { 2 } - 2 | x | = a $ 有 4 个实数根,则 $ a $ 的取值范围是______.
]

(1) 自变量 $ x $ 的取值范围是全体实数,$ x $ 与 $ y $ 的几组对应值如下表:
| $ x $ | …$ $ | $ - 3 $ | $ - \frac { 5 } { 2 } $ | $ - 2 $ | $ - 1 $ | $ 0 $ | $ 1 $ | $ 2 $ | $ \frac { 5 } { 2 } $ | $ 3 $ | …$ $ |
| $ y $ | …$ $ | 3 | $ \frac { 5 } { 4 } $ | 0 | $ - 1 $ | 0 | $ - 1 $ | $ m $ | $ \frac { 5 } { 4 } $ | 3 | …$ $ |
其中,$ m = $______.
(2) 根据表中数据,在如图所示的平面直角坐标系中描点,现已画出了函数图象的一部分,请画出该函数图象的另一部分.
(3) 进一步探究函数图象发现:
① 方程 $ x ^ { 2 } - 2 | x | = 0 $ 有______个实数根;
② 若关于 $ x $ 的方程 $ x ^ { 2 } - 2 | x | = a $ 有 4 个实数根,则 $ a $ 的取值范围是______.
]

答案:
【解析】:
(1)要求$m$的值,
需要将$x=2$代入函数$y=x^{2}-2|x|$中,
当$x=2$时,
$y=2^{2}-2×|2|$
$=4-4$
$=0$
所以,$m=0$。
(2)根据表中数据描点,
已知$x=2$和$x=\frac{5}{2}$时的点,
继续描出这些点,并用平滑曲线连接,形成完整的函数图象,图略。
(3)①方程$x^{2}-2|x|=0$,
可以分解为$|x|(|x|-2)=0$,
解得$|x|=0$或$|x|=2$,
即$x=0$或$x=\pm2$,
所以,方程有3个实数根。
②要使方程$x^{2}-2|x|=a$有4个实数根,
需要确定$a$的取值范围,
当$a=-1$时,方程$x^{2}-2|x|=-1$,
即$x^{2}-2|x|+1=0$,
解得$x=\pm1$,有两个实数根,
当$-1<a<0$时,方程$x^{2}-2|x|=a$的图像与$y=a$的图像有4个交点,
即方程有4个实数根,
综上所述,$a$的取值范围为$-1<a<0$。
【答案】:
(1)$m=0$;
(2)
(3)①3;②$-1<a<0$。
【解析】:
(1)要求$m$的值,
需要将$x=2$代入函数$y=x^{2}-2|x|$中,
当$x=2$时,
$y=2^{2}-2×|2|$
$=4-4$
$=0$
所以,$m=0$。
(2)根据表中数据描点,
已知$x=2$和$x=\frac{5}{2}$时的点,
继续描出这些点,并用平滑曲线连接,形成完整的函数图象,图略。
(3)①方程$x^{2}-2|x|=0$,
可以分解为$|x|(|x|-2)=0$,
解得$|x|=0$或$|x|=2$,
即$x=0$或$x=\pm2$,
所以,方程有3个实数根。
②要使方程$x^{2}-2|x|=a$有4个实数根,
需要确定$a$的取值范围,
当$a=-1$时,方程$x^{2}-2|x|=-1$,
即$x^{2}-2|x|+1=0$,
解得$x=\pm1$,有两个实数根,
当$-1<a<0$时,方程$x^{2}-2|x|=a$的图像与$y=a$的图像有4个交点,
即方程有4个实数根,
综上所述,$a$的取值范围为$-1<a<0$。
【答案】:
(1)$m=0$;
(2)

(3)①3;②$-1<a<0$。
查看更多完整答案,请扫码查看


